现代信号处理学习笔记（三）信号检测

通过观测数据判断信号是否存在，这一问题称为信号检测。

前言

一、统计假设检验

1、信号检测的基本概念

2、信号检测理论测度

比率测度

概率测度

3、决策理论空间

二、概率密度函数与误差函数

1、概率密度函数

2、误差函数与补余误差函数

三、检测概率与错误概率

1、定义

2、功效函数

四、Neyman-Pearson准则

五、一致最大功效准则

六、Bayes 准则

总结

前言

通过将信号检测视为统计假设检验问题，就可以采用一种通用的数学框架讨论和分析不同情况下的信号检测。本章正是从这一视角出发，对信号检测的有关理论、方法与应用展开讨论。

一、统计假设检验

从理论层面讲，信号检测理论(signal detection theory, SDT)是一种统计假设检验理论:通过分析来自实验的数据，对模棱两可的刺激源(或称响应)作出判决：它究竟是由某个已知过程产生的信号，抑或仅仅是噪声而已。信号检测理论广泛应用于差异悬殊的众多邻域。

1、信号检测的基本概念

传感过程由传输和感知两个过程组成:物理世界的信(号)源经过传输和转换，变成可以观测的数据;然后通过传感单元感知或观测。被感知的物理过程或现象称为刺激源，感知或传感结果称为观测数据。由于单个数据难以做出正确的统计决策，所以有必要使用一组观测数据，经由检测单元对该组观测数据做出统计推断或者决策。得到的推断或决策结果称为响应。这一响应通过显示单元输出。

从计算角度看，信号检测理论是一种计算框架(computational framework)，它描述如何从噪声中抽取信号，同时对可能影响抽取过程的偏差和其他因素作出解释。

在信号检测中，现实情况分为信号存在和不存在两种情况，其中信号不存在对应为噪声存在。决策或判决结果要么“是”(肯定)，要么“否”(否定)，为择一判决。因此，会出现以下四种判决结果:

真正(True Positive, TP):
说明信号存在，并且判决结果正确地肯定了信号的存在。
真负(True Negative, TN):
说明信号不存在，且判决结果正确地否定了信号的存在。
假正(False Positive, FP):
说明信号不存在，但判决结果错误地肯定了信号的存在，这通常称为“误报”或“假警报”。
假负(False Negative, FN):
说明信号存在，但判决结果错误地否定了信号的存在，这通常称为“漏报”或“假负警报”。

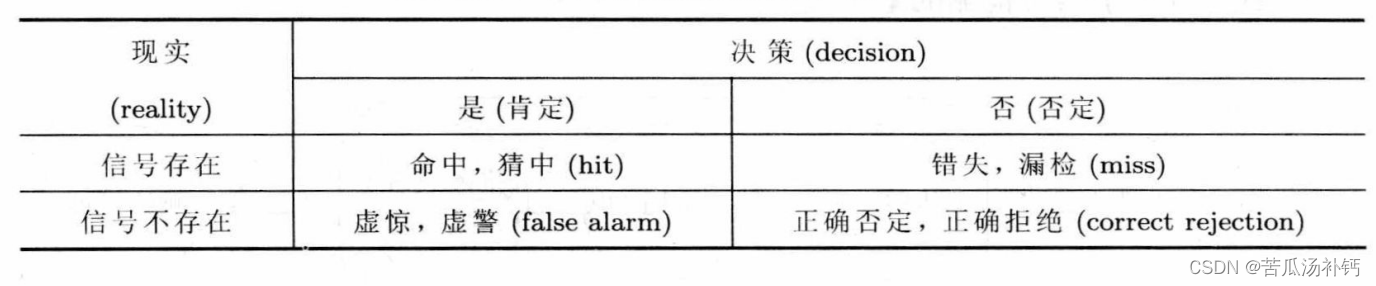
某个刺激源或响应在实验总次数所占的比例(proportion)又称频次(frequency)或者概率(probability)。

信号检测理论中的四种响应发生的相对频次不是彼此无关的。

信号与噪声识别的主要错误来源有以下三种:

刺激源可能超出了标准的可视窗口(信号≤噪声):例如紫外线，可视窗口减小(实验或者生理上的)，又如色盲等。
刺激源可能被外部噪声所“掩蔽”，造成信噪比减小。此时，又分为以下两种情况。噪声增大(外部噪声严重影响检测机制)或者空间/时间模糊性增加(例如泥浆溅射效应)。信号减小(外部噪声激活了抑制机制，导致信号的边缘掩蔽)。
换能器或传感器的变化(实验或神经诱导的增益控制效果规范化失败)。

2、信号检测理论测度

信号检测理论测度(SDT measure)可以用比率或者概率表示。

比率测度

使用比率表示的测度有命中率和虚警率。

命中率（Hit Rate）：命中率表示正确检测到信号的比率，即在信号存在的情况下正确地肯定了信号的存在。命中率可以用以下公式表示：

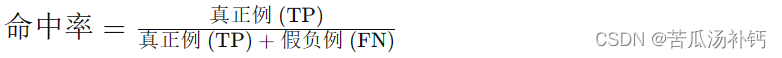
虚警率（False Alarm Rate）：虚警率表示在信号不存在的情况下错误地肯定了信号存在的比率，即假正例的比率。虚警率可以用以下公式表示：

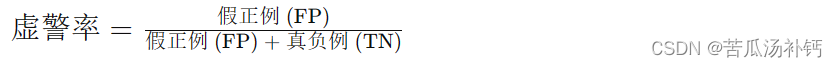
概率测度

使用概率表示的测度通常用函数形式表示，称为测度函数。测度函数有两种： $\o$ $\o$ $\o$ Φ函数和逆 $\o$ $\o$ Φ函数（inverse phi function)。

3、决策理论空间

整个决策理论空间由以下四个子空间组成:

S=信号或参数空间
Ω=观测样本空间
D=决策空间
A=行为或结果空间

二、概率密度函数与误差函数

概率密度函数（Probability Density Function, PDF）：

定义： 概率密度函数是用来描述随机变量的可能取值的概率分布的数学函数。对于连续型随机变量，概率密度函数是描述该变量在某一取值范围内的概率分布的函数。通常用符号 f(x) 表示。
特点： 概率密度函数必须满足两个条件，即在整个定义域内的取值必须是非负的，并且整个定义域上的积分等于1。

误差函数（Error Function）：

定义： 误差函数是一种特殊的数学函数，通常用 erf(x) 表示。在数学、工程和统计学等领域中经常用到误差函数，它描述了一个随机变量的误差在正态分布中的累积概率。
表达式： 误差函数的表达式如下：
特点： 误差函数的取值范围是在 -1 到 1 之间，而且它的图像呈 S 形，与正态分布的累积分布函数有关。

1、概率密度函数

总是令Ho,H1代表离散的随机事件，它们相互独立；而观测数据y1,…,yN为连续的随机变量。

2、误差函数与补余误差函数

三、检测概率与错误概率

1、定义

S1或者S0信号被正确判断，都属于二元假设检验的正确决策。正确决策发生的概率称为(信号的)检测概率(probability of detection)，分为以下两种类型。

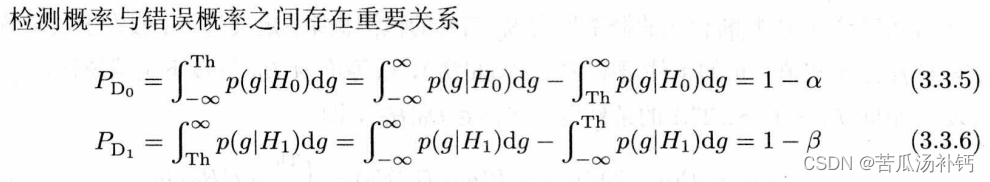
以上两个关系式的物理意义分别如下：

由于任何一个信号被正确和错误检测的总概率等于1，所以S0信号的正确检测概率PDo。很自然地应该是总检测概率1减去其错误检测概率α的结果，而S1信号的正确检测概率P，也很自然地等于总检测概率1减去其错误检测概率β。

2、功效函数

功效函数（Power Function）是统计假设检验中的一个重要概念。它与检验的显著性水平和样本大小相关，用来评估在某个统计检验下拒绝虚无假设的能力。在假设检验中，通常我们关注两个错误：第一类错误（Type I Error）和第二类错误（Type II Error）。

第一类错误（Type I Error）： 拒绝了一个实际上是正确的零假设。显著性水平（Significance Level）用来控制第一类错误的概率，通常表示为 α。
第二类错误（Type II Error）： 接受了一个实际上是错误的零假设。功效函数用来评估避免第二类错误的能力，通常表示为 1−β，其中 β 是第二类错误的概率。

功效函数（Power Function）定义为检验拒绝虚无假设的概率，给定实际上是真的备择假设成立。它通常用符号π(θ) 表示，其中 θ 是备择假设的参数。

π(θ)=P(拒绝 H0∣H1 是真的)

信号检测的对象可以分为三种类型，它们分别采用不同的决策准则。

四、Neyman-Pearson准则

在实际的信号检测中，有许多应用问题可以归类为这样一种二元假设检验：零假设检验Ho代表仅有噪声的假设，而备择假设检验H则代表观测数据中信号存在的假设。

Neyman-Pearson准则是统计假设检验中的一种方法，旨在在给定显著性水平下，使得检验的功效尽可能大。该准则是由统计学家Jerzy Neyman和Egon Pearson在20世纪20年代提出的。

Neyman-Pearson准则的基本思想是，对于一个给定的显著性水平 α（通常是0.05或0.01），我们设定一个拒绝域，使得在零假设为真时发生第一类错误（拒绝零假设，实际上零假设是正确的）的概率最小。同时，在备择假设为真时，检验的功效（避免第二类错误的能力）尽可能大。

Neyman-Pearson准则的步骤如下：

设定零假设 H0 和备择假设 H1。
确定显著性水平 α。
计算拒绝域。 Neyman-Pearson准则指导我们选择一个拒绝域，使得在零假设为真时发生第一类错误的概率最小。
计算功效。 在备择假设为真的条件下，计算检验的功效，即避免第二类错误的能力。

这种准则通常应用于二项分布或正态分布等常见分布的假设检验中。它强调在控制第一类错误概率的同时，尽量提高检验的功效。然而，需要注意的是，Neyman-Pearson准则通常较为严格，因为它在设计中需要明确规定拒绝域，并且可能忽略了其他一些信息。在实际应用中，研究人员可能需要综合考虑多个因素，选择适合特定问题的检验方法。

五、一致最大功效准则

一致最大功效准则（Uniformly Most Powerful (UMP) Test）是一种假设检验的原则，其目标是在所有可能的参数值下，检验的功效（避免第二类错误的能力）都是最大的。这个准则在统计推断的理论中起着重要的作用。

UMP检验有一致性的性质，即在样本大小趋向无穷大时，它的功效趋于1。具体来说，UMP检验满足以下性质：

零假设下的最大功效： 在所有可能的参数值下，UMP检验具有最大的功效，即在零假设为真时发生第二类错误的概率最小。
一致性： 随着样本大小的增加，UMP检验的功效趋于1，表现出对备择假设的高敏感性。

UMP检验的设计通常要考虑分布族的形式，具体的参数值，以及显著性水平。UMP检验不一定对于所有问题都是唯一的，而且在实际应用中，有时可能难以找到UMP检验。它通常与一些特定的分布族和假设条件相关。

UMP准则的使用通常需要对问题进行详细的数学分析，可能包括拉格朗日乘数法、对数似然比等高级数学工具。UMP检验在统计学理论的发展中发挥了重要作用，为制定具有最佳性能的检验提供了一种理论框架。

六、Bayes 准则

贝叶斯准则基于以下贝叶斯定理：

其中：

P(H∣D) 是在观测到数据 D 的条件下，假设 H 成立的后验概率。
P(D∣H) 是在假设 H 成立的条件下，观测到数据 D 的概率，即似然。
P(H) 是先验概率，即在观测到数据之前，对假设 H 的信念。
P(D) 是归一化常数，确保后验概率的总和为1。

基于这个定理，贝叶斯准则的决策规则可以概括为：

计算先验概率 P(H)： 在观测到数据之前，我们对不同假设的信念。
计算似然 P(D∣H)： 在给定各个假设的条件下，观测到实际数据的可能性。
计算后验概率 P(H∣D)： 根据观测到的数据，更新我们对不同假设的信念。
基于后验概率进行决策： 根据后验概率，选择具有最高概率的假设作为决策。

贝叶斯准则在处理不确定性和更新信息时非常有用，特别是在小样本情况下。然而，先验选择对于结果可能有较大的影响，这也是贝叶斯统计的一项挑战。

总结

通过观测数据判断信号是否存在，这一问题称为信号检测，它本质上是一种统计假设检验。所谓统计假设，就是关于我们感兴趣的一个总体的某个未知特征的主张。检验一个统计假设的根本任务即是：决定关于某个未知特征的主张是否为随机试验的观测样本所支持。通常，这一主张涉及的是采样的随机分布的某个未知参数或者某个未知函数。样本数据是否在统计意义上支持该主张的决定是根据概率作出的。简而言之，如果面对观测数据提供的证据，某个主张正确的机会大，就接受它；否则，便拒绝它。