文章目录
- ❇️Day 36 第八章 贪心算法 part05
- ✴️今日任务
- ❇️435. 无重叠区间
- 自己的思路
- 自己的代码(✅通过81.59%)
- 随想录思路
- 随想录代码
- ❇️763.划分字母区间
- 自己的思路
- 自己的代码(✅通过55.30%)
- 随想录思路
- 随想录代码
- ❇️56. 合并区间
- 自己的思路
- 自己的代码(82.47%)
- 随想录思路
- 随想录代码
❇️Day 36 第八章 贪心算法 part05
✴️今日任务
今天的三道题目,都算是 重叠区间 问题,大家可以好好感受一下。 都属于那种看起来好复杂,但一看贪心解法,惊呼:这么巧妙!
还是属于那种,做过了也就会了,没做过就很难想出来。
不过大家把如下三题做了之后, 重叠区间 基本上差不多了
- 435.无重叠区间
- 763.划分字母区间
- 56.合并区间
❇️435. 无重叠区间
- 题目链接:https://leetcode.cn/problems/non-overlapping-intervals/
- 视频讲解:https://www.bilibili.com/video/BV1A14y1c7E1
- 文章链接:https://programmercarl.com/0435.%E6%97%A0%E9%87%8D%E5%8F%A0%E5%8C%BA%E9%97%B4.html
自己的思路
还和452一样,通过先确定右区间再判断左区间的方式
区别:当重叠时count++
自己的代码(✅通过81.59%)
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
int count = 0;
Arrays.sort(intervals, new Comparator<int[]>() {
@Override
public int compare(int[] points1, int[] points2) {
if (points1[1] > points2[1]) {
return 1;
} else if (points1[1] < points2[1]) {
return -1;
}
return 0;
}
}
);
//for(int[] i :intervals) System.out.println(Arrays.toString(i));
int end = 0; //被取右区间的范围下标
int start = 1; //被取左区间的下标
while(start < intervals.length){
//System.out.println("次数:"+count);
//重叠
if(intervals[start][0] < intervals[end][1]){
count ++;
//System.out.println("气球{"+intervals[start][0]+", "+intervals[start][1]+"}可同时和气球{"+intervals[end][0]+", "+intervals[end][1]+"}一起被扎破");
}else{
end = start;
}
start ++;
}
return count;
}
}
随想录思路
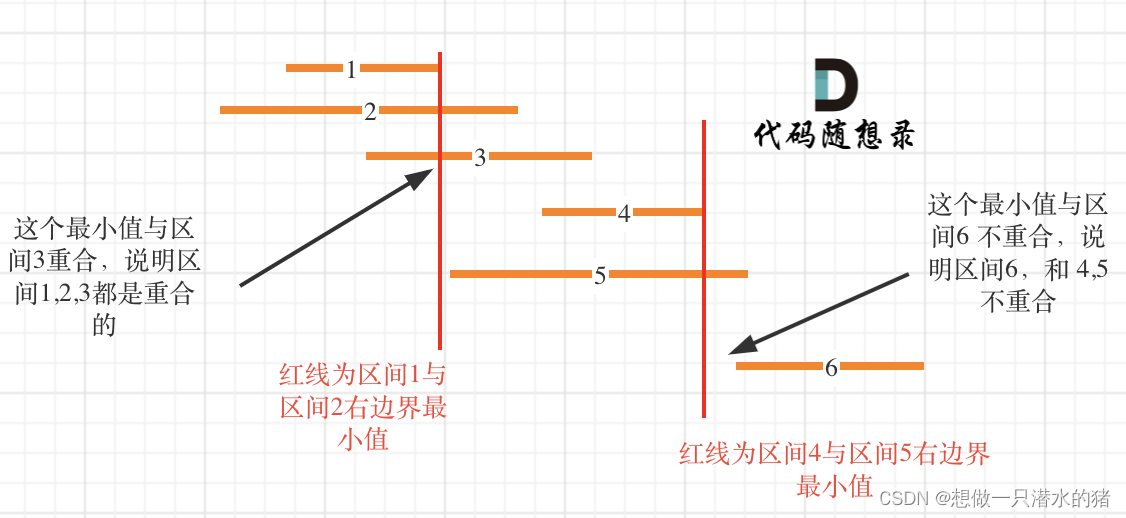
我来按照右边界排序,从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。
此时问题就是要求非交叉区间的最大个数。
这里记录非交叉区间的个数还是有技巧的,如图:
随想录代码
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals, (a,b)-> {
return Integer.compare(a[0],b[0]);
});
int count = 1;
for(int i = 1;i < intervals.length;i++){
if(intervals[i][0] < intervals[i-1][1]){
intervals[i][1] = Math.min(intervals[i - 1][1], intervals[i][1]);
continue;
}else{
count++;
}
}
return intervals.length - count;
}
}
❇️763.划分字母区间
- 题目链接:https://leetcode.cn/problems/partition-labels/
- 视频讲解:https://www.bilibili.com/video/BV18G4y1K7d5
- 文章链接:https://programmercarl.com/0763.%E5%88%92%E5%88%86%E5%AD%97%E6%AF%8D%E5%8C%BA%E9%97%B4.html
自己的思路
- 定义一个二维数组的数组int count[26][]来存储字母最开始出现的下标和最后出现的下标
- 遍历字符串得到每个字母出现的区间
- 定义最小左区间和最大右区间
自己的代码(✅通过55.30%)
class Solution {
public List<Integer> partitionLabels(String s) {
int count[][] = new int[26][2];
List<Integer> res = new ArrayList<>();
for (int i = 1; i < s.length(); i++) {
if(count[s.charAt(i)-'a'][1] == 0){
if(s.charAt(i) != s.charAt(0)) {
count[s.charAt(i) - 'a'][0] = i;
}
count[s.charAt(i)-'a'][1] = i;
}else{
count[s.charAt(i)-'a'][1] = i;
}
}
Arrays.sort(count, (a,b)-> {
return Integer.compare(a[0],b[0]);
});
int left = 0;
int right = count[0][1];
for (int i = 0; i < 26; i++) {
if(count[i][1] != 0) {
if(count[i][0] <= right){
right = Math.max(right, count[i][1]);
}else{
res.add(right - left + 1);
left = count[i][0];
right = count[i][1];
}
}
}
res.add(right - left + 1);
return res;
}
}
随想录思路
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
可以分为如下两步:
- 统计每一个字符最后出现的位置
- 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
如图:
![[图片]](https://img-blog.csdnimg.cn/direct/86d46bdae2c049ba97baff08d8cfa0a2.png)
随想录代码
class Solution {
public List<Integer> partitionLabels(String S) {
List<Integer> list = new LinkedList<>();
int[] edge = new int[26];
char[] chars = S.toCharArray();
for (int i = 0; i < chars.length; i++) {
edge[chars[i] - 'a'] = i;
}
int idx = 0;
int last = -1;
for (int i = 0; i < chars.length; i++) {
idx = Math.max(idx,edge[chars[i] - 'a']);
if (i == idx) {
list.add(i - last);
last = i;
}
}
return list;
}
}
❇️56. 合并区间
- 本题相对来说就比较难了
- 题目链接:https://leetcode.cn/problems/merge-intervals/
- 视频讲解:https://www.bilibili.com/video/BV1wx4y157nD
- 文章链接:https://programmercarl.com/0056.%E5%90%88%E5%B9%B6%E5%8C%BA%E9%97%B4.html
自己的思路
- 先对二维数组进行排序
- 判断后一个的左区间是否在前一个的右区间内
- 定义一个栈用来存放备选结果
自己的代码(82.47%)
public static int[][] merge(int[][] intervals) {
//当二维数组只有一个一维数组时返回该一维数组
if(intervals.length == 1) return intervals;
//定义一个结果二维数组
LinkedList<int[]> res = new LinkedList<>();
//count是结果二维数组的长度,当有重叠长度-1
int count = intervals.length;
//排序二维数组
Arrays.sort(intervals,(a,b) -> a[0] == b[0] ? a[1]-b[1] : a[0]-b[0]);
//定义当前右区间
int right = intervals[0][1];
//将第一个数组加入备选区间
res.push(intervals[0]);
//从第二个区间开始遍历
for (int i = 1; i < intervals.length; i++) {
//如果这个和上一个区间有重叠
if(intervals[i][0] <= right){
//长度--
count --;
//更新右区间
right = Math.max(intervals[i][1], right);
//更新备选区间的右区间
if(res.peek() != null && res.peek()[1] != right) {
res.peek()[1] = right;
}
}else{
//当没有重叠的时候直接加入备选区间
res.push(intervals[i]);
//更新用来对比的右区间
right = intervals[i][1];
}
}
return res.toArray(new int[count][]);
}
随想录思路
和我的基本一样
随想录代码
优化点:
- 栈的res.peek()可以换成res.removeLast();
- 可以去掉count,直接换成res.size()
public int[][] merge(int[][] intervals) {
LinkedList<int[]> res = new LinkedList<>();
Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));
res.add(intervals[0]);
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] <= res.getLast()[1]) {
int start = res.getLast()[0];
int end = Math.max(intervals[i][1], res.getLast()[1]);
res.removeLast();
res.add(new int[]{start, end});
}
else {
res.add(intervals[i]);
}
}
return res.toArray(new int[res.size()][]);
}





![[C语言]——C语言常见概念(2)](https://img-blog.csdnimg.cn/direct/eceea348a9ca4e3c8bcfe810fe9e4222.png)