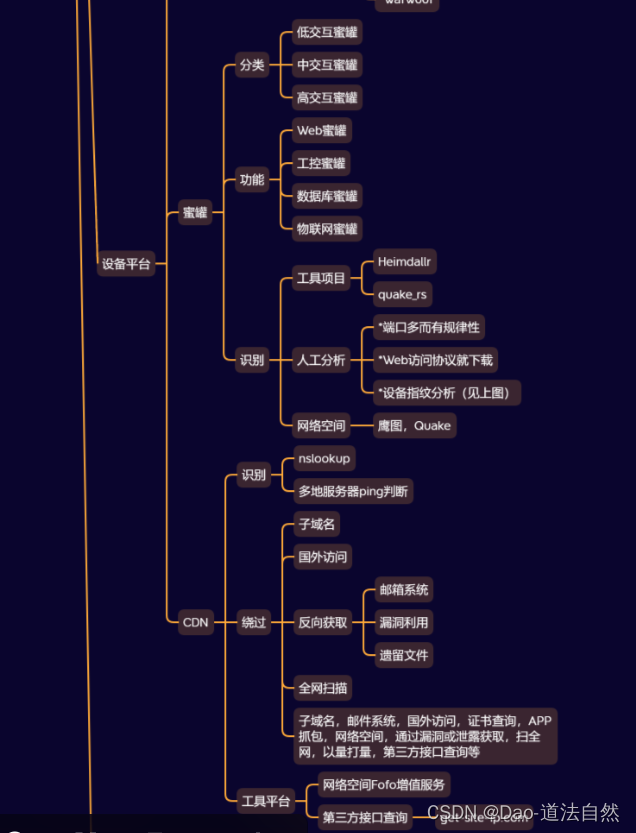
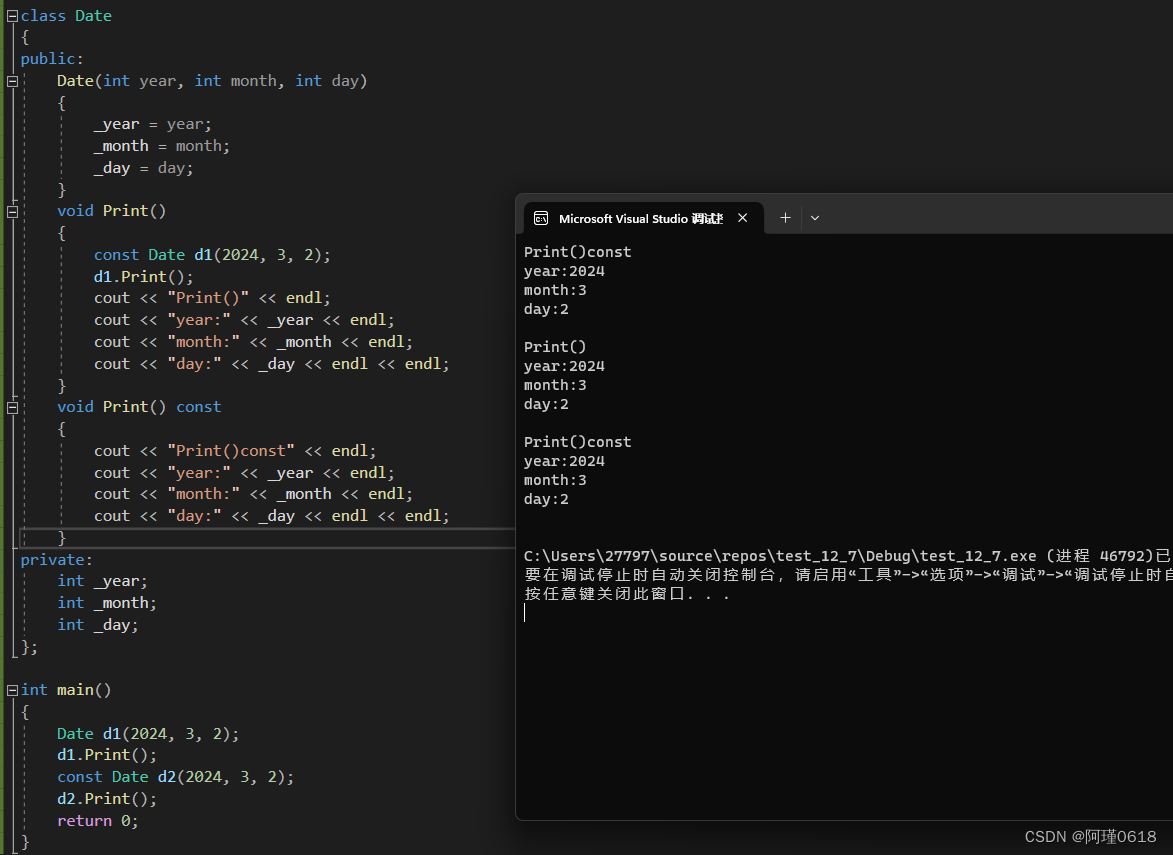
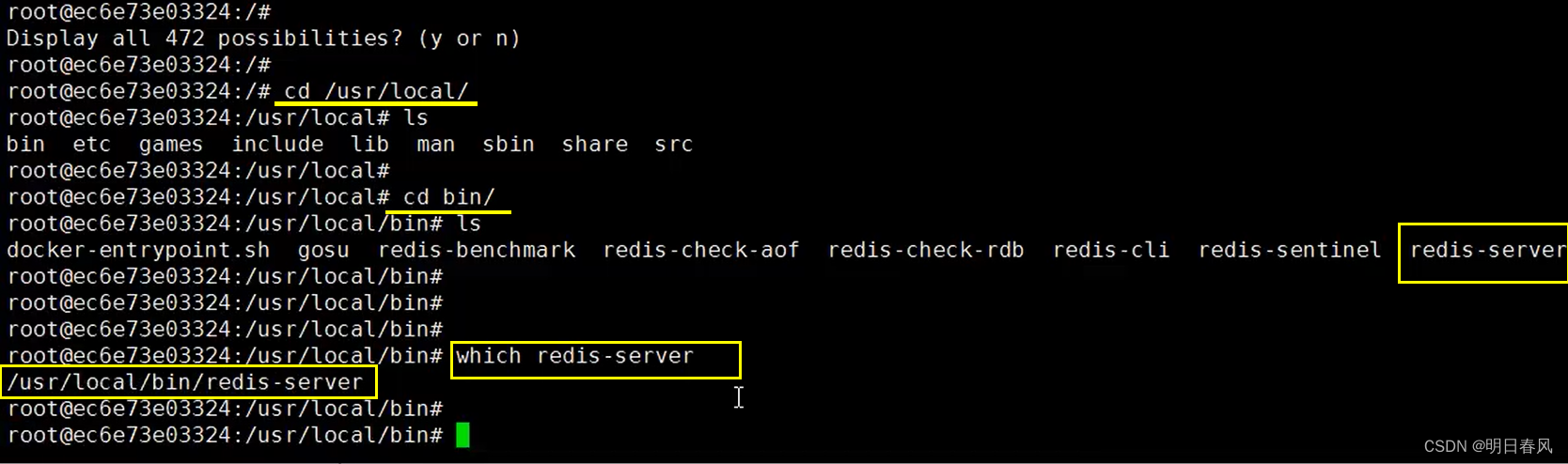
给出三条线段a,b,c 的长度，均是不大于 1000010000 的正整数。打算把这三条线段拼成一个三角形，它可以是什么三角形呢？

• 如果三条线段不能组成一个三角形，输出Not triangle；
• 如果是直角三角形，输出Right triangle；
• 如果是锐角三角形，输出Acute triangle；
• 如果是钝角三角形，输出Obtuse triangle；
• 如果是等腰三角形，输出Isosceles triangle；
• 如果是等边三角形，输出Equilateral triangle。

如果这个三角形符合以上多个条件，请按以上顺序分别输出，并用换行符隔开。

输入格式

输入 3 个整数 a、b 和c。

输出格式

输出若干行判定字符串。

输入样例1

3 3 3

输出样例1

Acute triangle
Isosceles triangle
Equilateral triangle

输入样例2

3 4 5

输出样例2

Right triangle

输入样例3

6 10 6

输出样例3

Obtuse triangle
Isosceles triangle

输入样例4

1 14 5

输出样例4

Not triangle

说明/提示

当两短边的平方和大于一长边的平方，说明是锐角三角形。

当两短边的平方和等于一长边的平方，说明是直角三角形。

当两短边的平方和小于一长边的平方，说明是钝角三角形。

解析：

首先，需要对三条边的长度进行排序，用一个d数组存储后sort一遍即可。

排序完之后看，如果最长的一条边大于等于另外两条边的长度和，则无法构成三角形。等腰三角形、等边三角形和直角三角形这些也都好判断，这里不再赘述。

最难的是锐角三角形和钝角三角形。可能大多数小学生和部分初中生都不知道如何判定锐角和钝角三角形。那首先把结论放在这里：

在一个三角形中，如果较短的两条边的平方和大于最长边的平方，那么这个三角形是锐角三角形，否则它是钝角三角形。

可能大多数题解都不会涉及这个结论的证明，那下面我来为大家证明一下。这个结论的证明需要涉及到余弦定理。

我们都知道，设三角形三个角的大小分别为∠A,∠B,∠C，三个角的对边分别为a,b,c，则有如下结论：

                                

                                

这就是余弦定理。

我们又知道：

又因为三角形每个角的度数都小于，所以当∠A时，所以上面这个式子就变成了：

                                       

                                        

当<∠时，，所以如上式子就变成了：

                                    

                                   

综上所述，当三角形任意两边平方和大于第三边的平方，说明这个三角形是锐角三角形，否则它就是钝角三角形。

证明完后，直接上code!

不准直接抄！！！

#include <iostream>
#include <algorithm>
using namespace std;
int a, b, c;
int main(){
	
	cin>>a>>b>>c;
	int d[4] = {0, a, b, c};
	sort(d + 1, d + 4);
	if(d[1] + d[2] <= d[3])
	{
		cout<<"Not triangle";
		return 0;
	}
	if(d[1] * d[1] + d[2] * d[2] == d[3] * d[3])
		cout<<"Right triangle";
	else if(d[1] * d[1] + d[2] * d[2] > d[3] * d[3])
		cout<<"Acute triangle";
	else if(d[1] * d[1] + d[2] * d[2] < d[3] * d[3])
		cout<<"Obtuse triangle";
	if(a == b || b == c || a == c)
		cout<<"Isosceles triangle";
	if(a == b && b == c)
		cout<<"Equilateral triangle\n";

	return 0;
}

 Ladies and gentlemen，赶紧用你发财的小手点个赞吧！