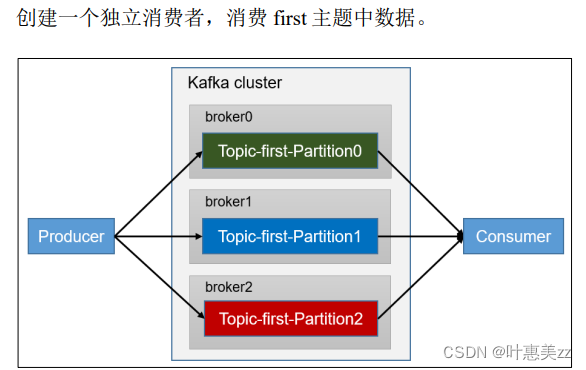
Grid-Based Continuous Normal Representation for Anomaly Detection 论文阅读
- 摘要
- 简介
- 方法
- 3.1 Normal Representation
- 3.2 Feature Refinement
- 3.3 Training and Inference
- 4 实验结果
- 5 总结
文章信息:

原文链接:https://arxiv.org/abs/2402.18293
源码地址:https://github.com/laozhanger/GRAD
摘要
最近在无监督方式下,异常检测领域取得了重大进展,其中仅有正常图像用于训练。几种最新的方法旨在基于记忆检测异常,通过比较输入和直接存储的正常特征(或使用正常图像训练的特征)。然而,这种基于记忆的方法在离散特征空间上操作,通过最近邻或注意机制实现,存在泛化能力差或者输出与输入相同的身份捷径问题。此外,现有方法中大部分设计用于检测单一类别的异常,当面对多类别对象时性能不理想。为了解决上述所有挑战,
我们提出了GRAD,一种新颖的异常检测方法,用于在“连续”特征空间中表示正常特征,通过将空间特征转换为坐标并将其映射到连续网格来实现。
此外,我们精心设计了专为异常检测定制的网格,有效表示局部和全局正常特征,并有效地融合它们。
我们的大量实验证明,GRAD成功地泛化了正常特征并减轻了身份捷径问题,此外,由于高粒度全局表示,GRAD有效地处理了单一模型中的多样类别。
在使用MVTec AD数据集进行评估时,GRAD在多类别统一异常检测方面减少了65.0%的错误,显著优于先前的最先进方法。项目页面位于 https://tae-mo.github.io/grad/。
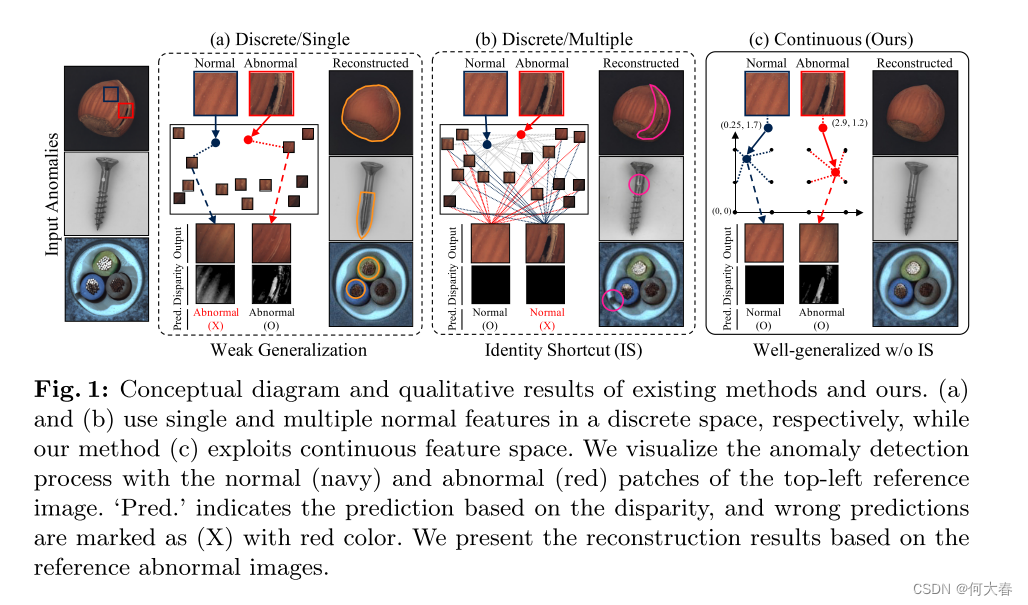
简介
在这项工作中,作者提出了将网格表示结合到异常检测中以实现高性能。
主要贡献:通过将离散特征存储替换为连续网格来表示正常特征,从而解决了上述讨论的挑战性问题,并实现了高性能。
方法
Background.为了帮助读者理解GRAD,我们首先描述了网格操作。网格被训练为坐标的函数,具有无限分辨率,输出与坐标对应的特征。无限分辨率下的输出特征是通过网格中附近特征的聚合得到的,基于输入坐标和相邻特征之间的距离。例如,当我们进行一维网格采样
ϕ
(
⋅
;
G
)
:
R
→
R
C
ϕ(·; G) : \mathbb{R} → \mathbb{R}^C
ϕ(⋅;G):R→RC 时,具有C个通道的输出特征是通过一维网格
G
∈
R
R
×
C
G ∈ \mathbb{R}^{R×C}
G∈RR×C 的相邻值进行插值得到的,数学上可以表示如下:
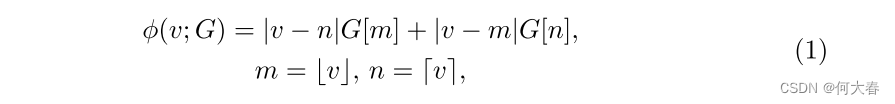
其中,
v
∈
R
v ∈ \mathbb{R}
v∈R 是一个任意的输入坐标,被归一化为网格分辨率
R
R
R,而
G
[
i
G[i
G[i] 表示来自网格
G
G
G 的索引
i
i
i 处的特征。
m
m
m 和
n
n
n 是要参考的索引,
⌊
⋅
⌋
⌊·⌋
⌊⋅⌋ 和
⌈
⋅
⌉
⌈·⌉
⌈⋅⌉ 分别表示向下取整和向上取整操作。上述方程可以通过对D维网格的
2
D
值
2^D值
2D值进行插值,简单地扩展到更高维度
D
D
D(例如,在图1( c )中的2D网格中的4个值)。
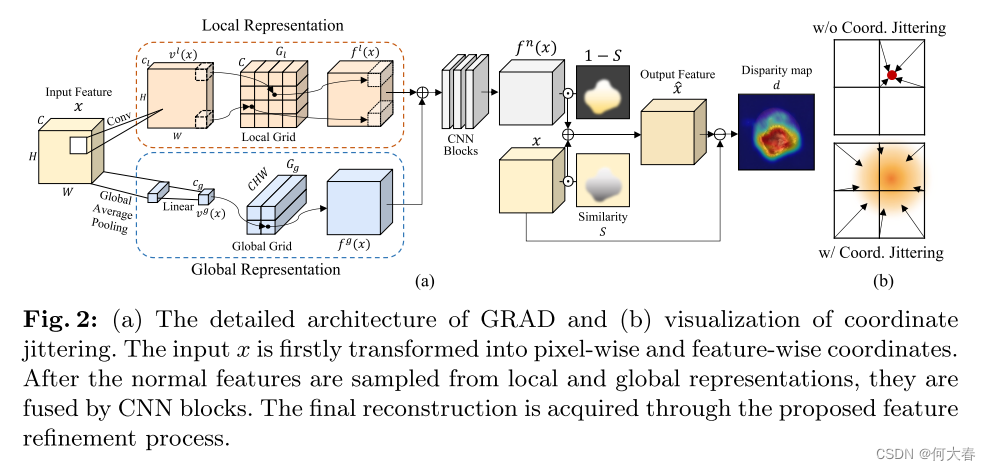
Overview.我们的工作动机是利用网格操作在连续空间中有效表示正常特征,与离散空间有所区别。以无监督的方式,GRAD基于输入特征和输出正常特征之间的差异来检测异常图像和区域,如图2(a)中所描述的。因此,GRAD的主要目标是有效地保留正常成分(例如,形状或纹理),同时消除特征内存在的任何异常。
为此,我们在训练阶段将正常特征表示为连续空间中的正常表示,这在测试阶段用于替换异常特征。我们描述了GRAD如何在连续空间中表示正常特征并获取输出特征 x ^ \hat{x} x^,基于从预训练骨干网络提取的输入特征 x x x,其中 x x x, x ^ ∈ R C × H × W \hat{x} ∈ \mathbb{R}^{C×H×W} x^∈RC×H×W, C 、 H 、 W C、H、W C、H、W 分别是特征的通道数、高度和宽度。
3.1 Normal Representation
GRAD的基本概念是将输入特征转换为连续值的特定坐标,然后将这些坐标映射到特征网格上。特别地,我们设计了从局部和全局视角表示正常特征。通过结合每个视角的独特特征,得到的特征可以提供对输入的强大表示,捕捉细粒度的细节以及更广泛的整体结构。
Local representation.
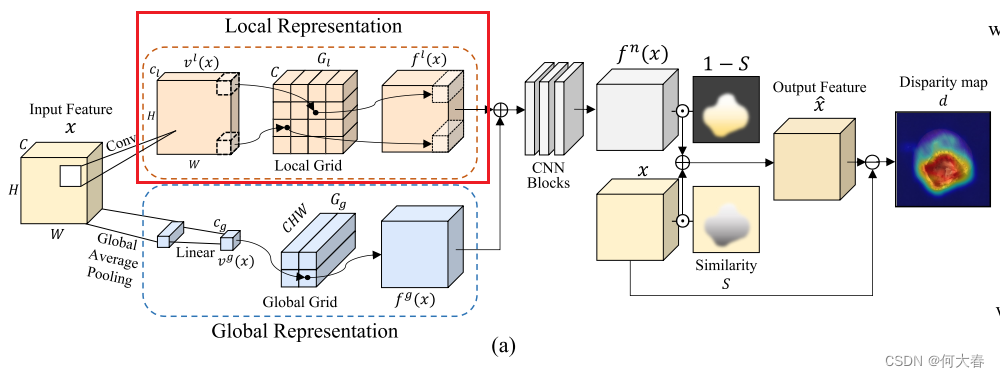
如图2(a)所示,GRAD对特征的每个像素进行采样,以表征图像的每个补丁,以表示局部特征。然后,通过具有1个卷积核大小的卷积层将每个像素的通道转换为相应的坐标(低维向量),然后进行双曲正切激活。利用这些逐像素的坐标,我们从局部网格表示中获取采样的正常特征。更正式地,我们定义一个函数
v
l
(
⋅
)
:
R
C
×
H
×
W
→
R
C
l
×
H
×
W
v^l(·) :\mathbb{R}^{C×H×W} → \mathbb{R}^{C_l×H×W}
vl(⋅):RC×H×W→RCl×H×W,根据输入特征生成逐像素的坐标,其中
C
l
C_l
Cl是生成坐标的维度。给定逐像素的坐标
v
h
,
w
l
(
⋅
)
∈
R
C
l
v^l_{h,w}(·) ∈ \mathbb{R}^{C_l}
vh,wl(⋅)∈RCl,从具有每个维度分辨率
R
l
R_l
Rl和通道数
C
C
C的
C
l
C_l
Cl维网格
G
l
G_l
Gl中采样正常特征。局部表示
f
l
(
x
)
:
R
C
×
H
×
W
→
R
C
×
H
×
W
f^l(x) : \mathbb{R}^{C×H×W} → \mathbb{R}^{C×H×W}
fl(x):RC×H×W→RC×H×W 的方程如下所示:
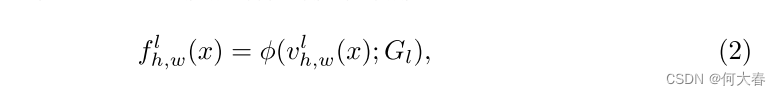
其中,
ϕ
(
⋅
;
G
l
):
R
C
l
→
R
C
ϕ(·; G_l):\mathbb{R}^{C_l}→\mathbb{R}^C
ϕ(⋅;Gl):RCl→RC表示通过基于坐标对网格值进行双线性内插来从网格
G
l
G_l
Gl采样特征。
由于特征的每个像素都表征图像中的一个补丁,局部表示确保保留正常补丁,并用具有相似局部上下文的正常补丁替换异常补丁。因此,当输入一个正常补丁时,即使在训练补丁中没有完全匹配的情况下,也可以通过插值映射到附近坐标的正常特征来表示相应的正常特征。
此外,对于异常补丁,GRAD基于减少的坐标找到一个最能代表异常补丁的正常特征。由于在训练过程中网格从未暴露于异常特征,它无法通过插值附近的正常特征来表示异常特征。这是我们如何有效解决现有方法中经常出现的基于注意机制聚合大量特征的相似性而产生的身份捷径(IS)问题的核心思想。
Global representation.异常区域不仅可能存在于图像的局部,还可能存在于全局范围内。为了处理这样的全局异常情况,GRAD维护另一个网格表示来捕获图像的全局特征。与局部表示类似,我们制定了一个函数来获取全局特征坐标
v
g
(
⋅
)
:
R
C
×
H
×
W
→
R
C
g
v^g(·) : \mathbb{R}^{C×H×W} → \mathbb{R}^{C_g}
vg(⋅):RC×H×W→RCg ,其中
C
g
C_g
Cg是坐标的降维维度。对于函数
v
g
(
⋅
)
v^g(·)
vg(⋅),我们采用了全局平均池化和线性层,如图2(a)所示。特征级的坐标通过具有每个维度分辨率
R
g
R_g
Rg的
C
g
C_g
Cg维网格
G
g
G_g
Gg映射到每个正常特征。网格
G
g
G_g
Gg的一个元素是一个
C
H
W
CHW
CHW维向量,一旦被采样,它就被重塑为
C
×
H
×
W
C×H×W
C×H×W张量。全局表示
f
g
(
x
)
:
R
C
×
H
×
W
→
R
C
×
H
×
W
f^g(x) : \mathbb{R}^{C×H×W} → \mathbb{R}^{C×H×W}
fg(x):RC×H×W→RC×H×W的方程表示如下:
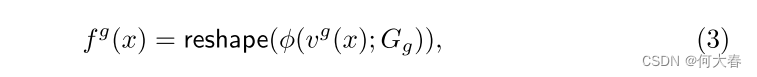
其中,
ϕ
(
⋅
;
G
g
):
R
C
g
→
R
C
H
W
ϕ(·; G_g):\mathbb{R}^{C_g}→\mathbb{R}^{CHW}
ϕ(⋅;Gg):RCg→RCHW表示通过双线性插值从网格
G
g
G_g
Gg采样特征,并且
r
e
s
h
a
p
e
(
⋅
):
R
C
H
W
→
R
C
×
H
×
W
reshape(·):\mathbb{R}^{CHW} → \mathbb{R}^{C×H×W}
reshape(⋅):RCHW→RC×H×W表示整形操作。
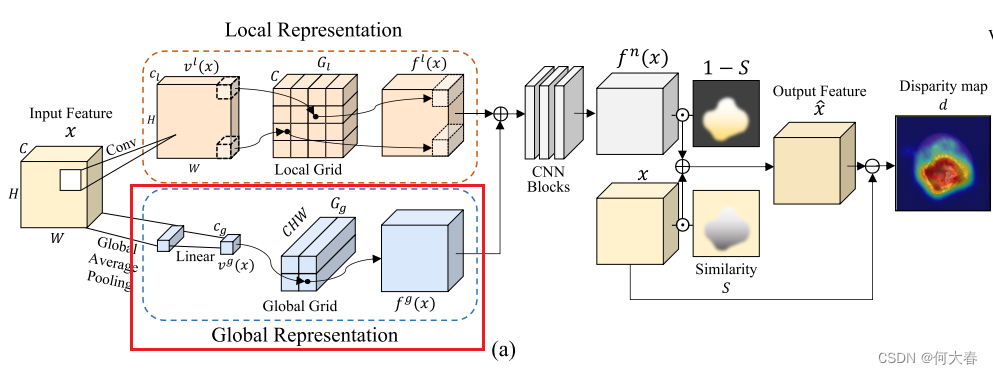
Fused representation.我们将局部和全局表示
f
l
(
x
)
f_l(x)
fl(x)和
f
g
(
x
)
f_g(x)
fg(x)组合起来,以有效地学习正常表示
f
n
(
x
)
f_n(x)
fn(x),如图2(a)所示。局部和全局表示被连接起来,然后被送入以下卷积网络
ψ
(
⋅
)
:
R
2
C
×
H
×
W
→
R
C
×
H
×
W
ψ(·) : \mathbb{R}^{2C×H×W} → \mathbb{R}^{C×H×W}
ψ(⋅):R2C×H×W→RC×H×W来重构
f
n
(
x
)
f_n(x)
fn(x),如下所示:
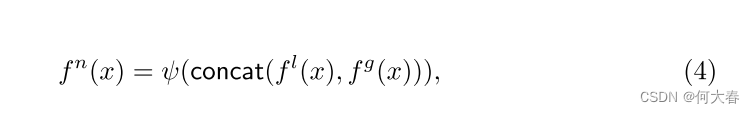
其中, c o n c a t ( ⋅ , ⋅ ) concat(·, ·) concat(⋅,⋅)表示沿着通道轴拼接两个特征。通过融合局部和全局表示,GRAD可以从细粒度的细节到更广泛的上下文中表示正常特征,相比仅使用其中之一,可以获得更高的性能(见第4.4节中的消融研究)。
3.2 Feature Refinement
尽管局部和全局正常表示已经融合,但在
f
n
(
x
)
f_n(x)
fn(x)和
x
x
x之间仍然可能存在正常区域的偏差,这可能导致错误检测(即假阳性)。因此,在特征细化中,我们的目标是在应该是正常但与
x
x
x有偏差的区域中对
f
n
(
x
)
f_n(x)
fn(x)进行细化,以减少假阳性。为了识别这样的区域,我们通过结合均方误差(MSE)和余弦相似度评估
x
x
x和
f
n
(
x
)
f_n(x)
fn(x)之间的逐像素相似性。这两个指标提供了正常和异常特征之间差异的全面视角,其中
M
S
E
MSE
MSE捕捉绝对强度差异,而余弦相似度则表征结构和位置的相似性。通过考虑组合相似性
S
∈
R
H
×
W
S ∈ R^{H×W}
S∈RH×W,我们可以重构
x
^
\hat{x}
x^如下:
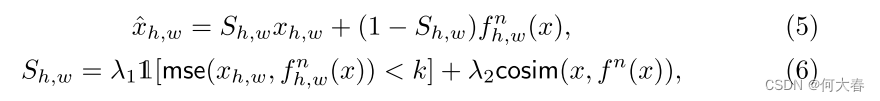
其中,
h
h
h和
w
w
w是空间特征的索引,
1
[
⋅
]
\mathbb{1}[·]
1[⋅]是指示函数,
m
s
e
(
⋅
,
⋅
)
mse(·, ·)
mse(⋅,⋅)和
c
o
s
i
m
(
⋅
,
⋅
)
cosim(·, ·)
cosim(⋅,⋅)分别是均方误差和余弦相似度。为了将MSE作为相似性的度量,我们根据其是否超过阈值k将MSE值转换为0或1。
3.3 Training and Inference
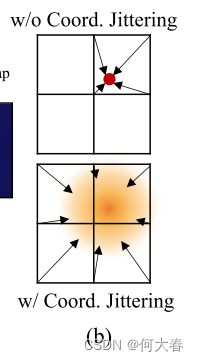
Coordinate jittering.为了实现更广义的网格表示,我们在训练阶段对局部坐标
v
l
(
x
)
v_l(x)
vl(x) 应用高斯噪声。例如,没有抖动时,在二维网格中,一个坐标影响最多四个网格值,如图2(b)所示。相比之下,当扰动坐标时,我们可以在每次迭代中使用钟形分布更新更多的网格值,从而产生更广义的网格。
Training.
给定
x
x
x和GRAD导出
x
^
\hat{x}
x^,我们采用MSE损失作为目标函数,如下所示:

根据公式(7),我们以端到端的方式学习整个模型,包括由Xavier正态初始化[12]初始化的网格。由于在训练阶段
x
x
x始终是正常输入,因此网格被学习用于表示正常特征。
Inference.
为了通过
x
x
x和
x
^
\hat{x}
x^之间的差异进行异常检测和定位,我们制定了异常分数图
d
∈
R
H
×
W
d ∈ \mathbb{R}^{H×W}
d∈RH×W如下所示:
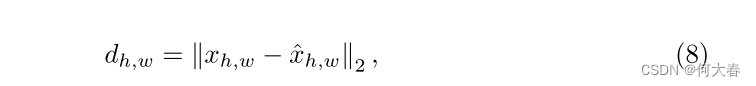
其中,
h
h
h和
w
w
w表示每个像素的位置。为了与相应的真实情况相匹配,
d
d
d被插值到输入的原始形状中。通过从平均池化的
d
d
d中取最大值,可以获得每个图像的异常分数,并且插值后的异常图本身用于像素级异常分数。
4 实验结果
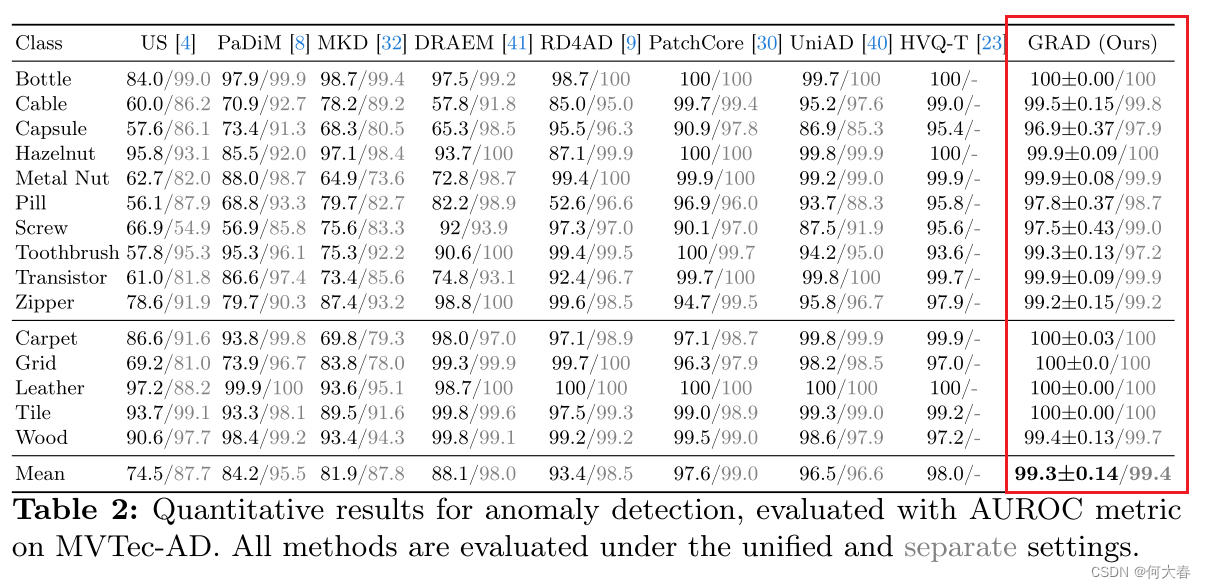
异常检测
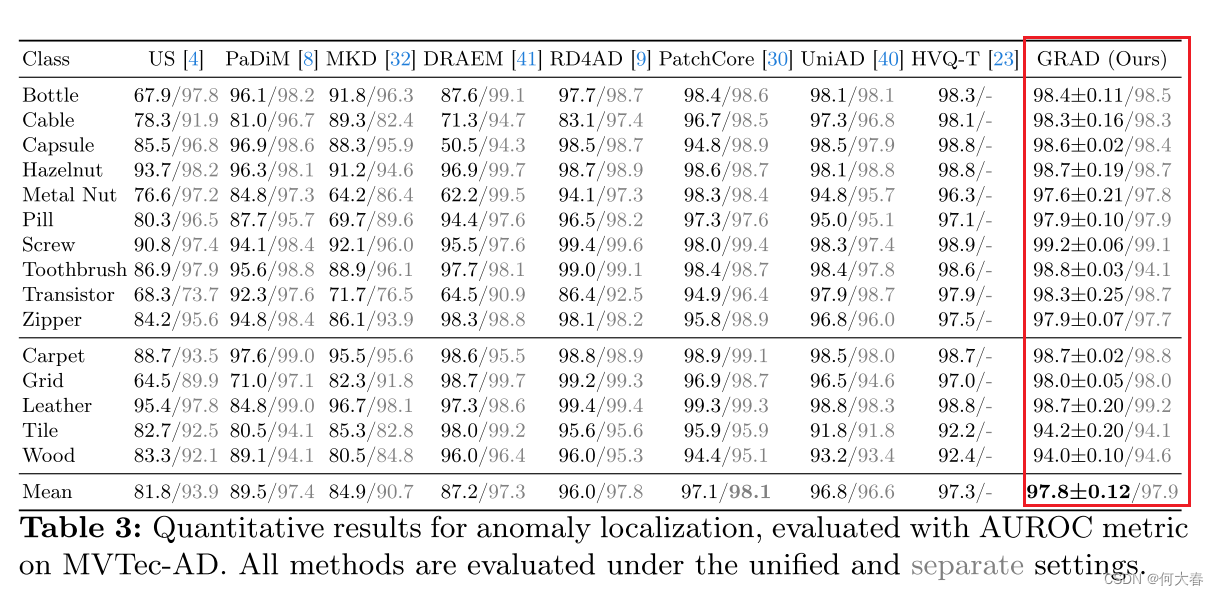
异常定位
5 总结
在这项工作中,作者提出了一种新颖的异常检测架构,名为GRAD,它在连续空间中表示正常特征,与之前局限于离散空间的方法不同。GRAD成功地在连续空间中表示了局部和全局特征,同时克服了现有方法的诸多局限,如泛化能力弱、身份捷径、计算复杂度和参数效率等。通过大量实验,作者定性和定量地展示了GRAD的有效性。通过特征细化和坐标抖动,GRAD取得了显著优势的最先进性能。










![LeetCode 刷题 [C++] 第226题.翻转二叉树](https://img-blog.csdnimg.cn/direct/b95f6cf4db03439380eca20a6b2eecfa.png)