目录
一、理论分析
二、程序介绍
1.基本环矩阵M的matlab代码
2.智能算法重构代码
三、下载链接
配网重构中,很重要的一个约束条件为配网应随时保持开环、辐射的状态: 配电网系统是属于闭环设计但是开环运行的系统,因此,在开关的开闭过程中,随时保持配电网的开环状态时很重要。Mendoza等利用图论,尤其是基本环向量的方法,不仅仅有效地保持了网络的辐射性,还大大地节省了搜寻时间和空间。还有文献对如何利用基本环向量去创造可行解的规则进行了详细阐述,文 中定义了基本节点,外节点,内节点,环向量,基本支路向量以及禁止的组向量 避免不可行解。本文中,应用了一个更加简单但同样有效的基于基本环向量的 方法保持配电网的开环,下面将进行详细阐述:
目录
一、理论分析
二、程序介绍
1.基本环矩阵M的matlab代码
2.智能算法重构代码
完整粒子群算法的重构程序代码链接
一、理论分析
本文中算例采用的是IEEE 33节点系统,因此以IEEE 33节点系统为例说明,配网中保持配网辐射状态的方法,IEEE 33节点系统有33个节点,32个分段开关和5个联络开关,为了使得网络保持辐射运行状态,具体的步骤如下:
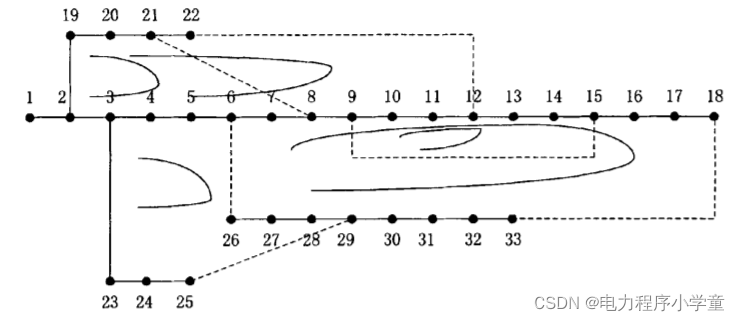
1.将系统中的各个支路进行标号,0代表支路上的开关是断开的,1代表支 路上的开关是闭合的; 2.利用图论决定基本的环路,环路的个数与联络开关的个数是一样的,对33 节点系统而言即5个,如下图所示。
![]()
3.然后,根据基本的环路列出基本环矩阵M。 M的行数即基本环的个数, 列数为支路数最多的那个环的支路数,其他小一些的环中没有这么多支路的空余 的地方值都填充为0。本文中,为了更简便,每条支路,包括环共有的支路,都只会包含在一个支路环里,这样就省略了节点分类以及还需创建其他支路的麻烦。 编码的规则是从图的最上面的支路编码到最下面的支路,从最左边的支路编码到最右边的支路。公共的支路只会被包含在首次将其编码进去的环内。通过上面的 编码即得到IEEE 33节点的基本环矩阵M:
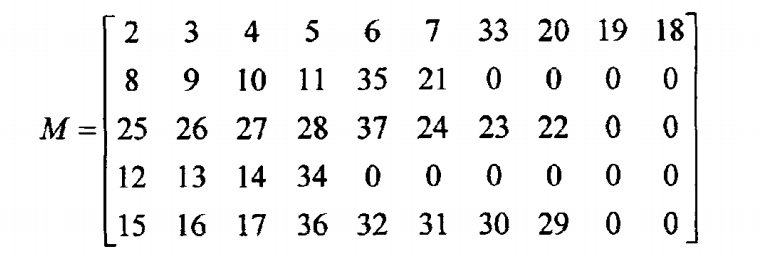
4.从矩阵M的每一行中选取一个非零元素,在每一次的网络重构中,每个环路中的都有且只有一条支路(非零元素)能被选为断开,每个环中被选中的断开的支路开关状态改为0,其余支路的开关状态都保持为1。
通过上面的步骤,在重构过程中没有非可行解的产生,因此整个重构过程的步骤大大简化。
二、程序介绍
上述理论非常适合应用于智能算法的配电网重构中,首先需要通过配电网参数形成M矩阵,具体代码如下:
1.基本环矩阵M的matlab代码
%产生回路编号矩阵M
b=32; %支路数,开断开关数
n=33; %节点数
LL=5; %联络开关数
Sb=10; %MW
Vb=12.66; %KV
Zb=Vb^2/Sb; %ohm
% 定义节点到母节点路径矩阵A
A=zeros(b); %对矩阵A进行初始化
for i=1:b
A(i,1)=i; %将路径矩阵A的第一列储存为支路号
end
for j=1:b %利用Z矩阵中的首末节点列向量进行路径搜索
n1=j;
k=2;
while(j~=0) %一直搜寻到母节点0结束
for m=1:b
if(Z(m,3)==j) %在末节点定位j
A(n1,k)=Z(m,2);
j=Z(m,2); %将首节点赋给j,然后再在末节点定位j
k=k+1;
end
end
end
end
%遍历A矩阵形成单回路矩阵H
for i=1:LL
jd=max(intersect(A(C(i,2),:),A(C(i,3),:))); %取回路交叉点jd,保证是单回路
h=1;
while(A(C(i,2),h)~=jd)
M(i,h)=A(C(i,2),h);
h=h+1;
end
h1=1;
while(A(C(i,3),h1)~=jd)
M(i,h)=A(C(i,3),h1);
h=h+1;
h1=h1+1;
end
M(i,h)=C(i,1);
end
![]()
2.智能算法重构代码
如粒子群算法中,变量可以选取M矩阵每行中的非零元素,通过迭代得到最佳的重构后网络,重构子函数如下所示。
%该为智能算法程序计算子函数,加入不可行解判断程序(在指定节点处加入DG)
b=32;
k=1;
n=33;
LL=5; %联络开关数 z
Sb=10; %MW
Vb=12.66; %KV
Zb=Vb^2/Sb; %ohm
check=1;
checkhl=1;
checkgd=1;
H=[ 2 3 4 5 6 7 33 20 19 18 0 0 0 0 0 0 0 0 0 0 0
9 10 11 12 13 14 34 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 3 4 5 6 7 8 9 10 11 35 21 20 19 18 0 0 0 0 0 0
6 7 8 9 10 11 12 13 14 15 16 17 36 32 31 30 29 28 27 26 25
3 4 5 25 26 27 28 37 24 23 22 0 0 0 0 0 0 0 0 0 0];%由函数matrixH生成
for i1=1:LL
a(1,i1)=H(i1,Swarm1(1,i1));
end
%1、判断是否形成环路,F为支路环路关联矩阵(行表示回路,列表示断开开关,若任意两行相同,则表示形成了环路)
F=zeros(5);
for i1=1:LL %回路
for i2=1:LL %断开开关
if max(a(1,i2)==H(i1,:))
F(i1,i2)=1;
end
end
end
for i1=1:LL-1
for i2=i1+1:LL
if min(F(:,i1)==F(:,i2))
checkhl=0; %disp('出现环路')%出现环路时
guan=10000;
end
end
end
for i1=1:LL %按照断开开关矩阵,剔除Z矩阵中的断开支路
j=i1-1;
for i2=1:b+LL-j
if BranchM(i2,1)==a(1,i1)
BranchM(i2,:)=[];
break
end
end
end
NodeN=zeros(n); %节点-节点关联矩阵A
for i1=1:b
NodeN(BranchM(i1,2),BranchM(i1,3))=1;
NodeN(BranchM(i1,3),BranchM(i1,2))=1;
end
LayerM=[1]; %节点分层矩阵,电源节点号记“1”
NU=zeros(1,n); %上层节点矩阵(有33列的行矩阵)
三、下载链接
![]()