1.1 简单线性回归

1. 简介

简单线性回归（SLR - Simple Linear Regression）模型可以表示为：$Y={\beta }_0+{\beta }_{1}X+ϵ$

• $Y$：因变量或目标变量。
• $X$：自变量或解释变量。
• ${\beta }_0$：截距项，是当$X=0$时$Y$的期望值。
• ${\beta }_1$：斜率项，表示$X$每变化一个单位，$Y$变化的量。
• $ϵ$​：误差项，表示模型未能解释的随机变异。

关于$ϵ$的解释

假设你是一位经济学家，正在研究家庭年收入（因变量 $Y$）与家庭主要收入者的教育年数（解释变量 $X$）之间的关系。你决定使用简单线性回归模型来分析这两个变量之间的关系。模型可以表示为：$Y={\beta }_0+{\beta }_{1}X+ϵ$其中：

• $Y$ 表示家庭年收入。
• $X$ 表示家庭主要收入者的教育年数。
• ${\beta }_0$ 是截距项，代表了当教育年数为0时预期的家庭年收入。
• ${\beta }_1$ 是斜率项，表示教育年数每增加一年，家庭年收入平均增加的金额。
• $ϵ$ 是误差项，代表了除了教育年数之外影响家庭年收入的所有其他因素。

例子说明

在现实中，家庭年收入受到多种因素的影响，除了教育年数之外，还可能包括行业、工作经验、地区、经济环境、健康状况等。由于我们的模型仅考虑了教育年数这一变量，因此模型无法完全解释家庭年收入的所有变化。这些未被模型捕捉的因素就通过误差项 $ϵ$ 来表示。

2. 例子与底层的手动实现

现在我们根据一个例子来深入理解简单线性回归。

**题目描述：**假设你是一位经济学家，正在研究家庭年收入（因变量 $Y$）与家庭主要收入者的教育年数（解释变量 $X$）之间的关系。你决定使用简单线性回归模型来分析这两个变量之间的关系。你收集了 10 个家庭的数据，如下所示：
[10, 12, 8, 15, 16, 18, 20, 14, 15, 11, 15, 19, 20]
[40, 45, 32, 50, 55, 65, 75, 48, 50, 38, 52, 70, 80]

将其使用散点图显示如下：

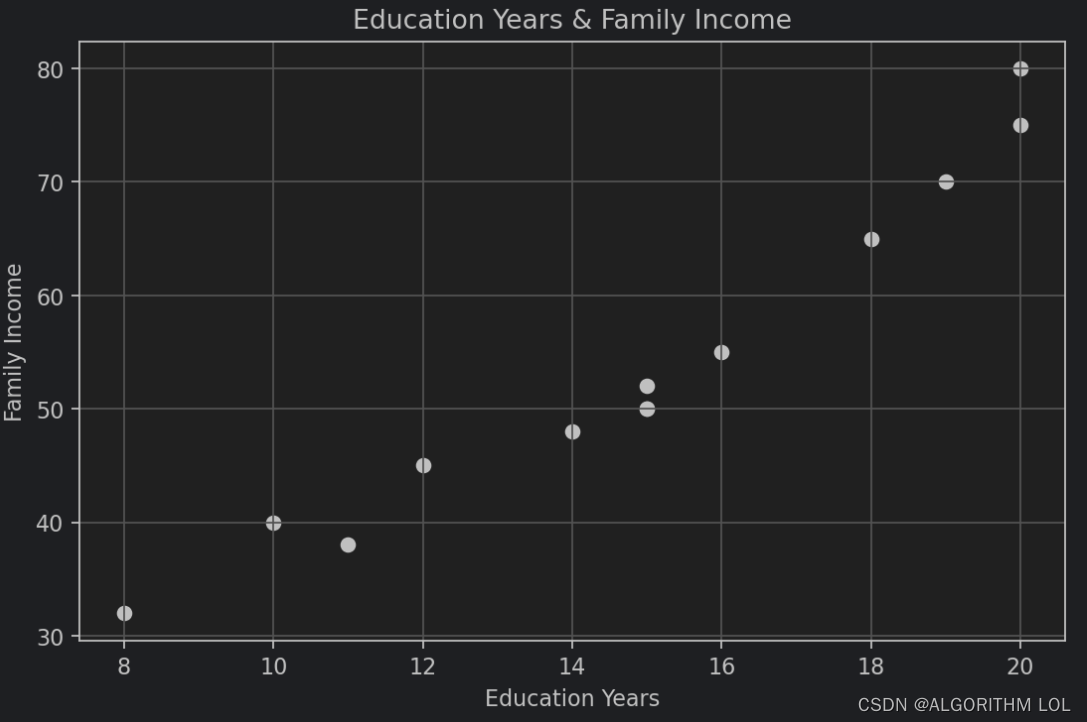
那么不使用scikit-learn库，手动实现简单线性回归，想一想如果想要用一条直线拟合这些点，我们需要计算些什么？

大家应该都很了解直线**，要确定一条直线，需要一个斜率，需要一个截距。**在这里我们就需要提到最小二乘法。

最小二乘法（Least Squares Method）

最小二乘法是一种常用的数学优化方法，用于求解线性回归等问题中的最优参数。其核心思想是通过最小化观测数据与模型预测之间的残差平方和来估计参数。

在线性回归问题中，假设我们有一组观测数据 $(x_i,y_i)$，其中 $x_i$ 是自变量（特征），$y_i$ 是因变量（目标值）。我们希望找到一个线性模型 $y=f(x)$，其中 $f(x)$ 是关于 $x$ 的线性函数，使得模型预测值 $f(x_i)$ 与观测值 $y_i$ 之间的误差最小化。最小二乘法通过求解以下优化问题来找到最优的模型参数：

$$\underset{\beta }{\min }\sum _{i=1}^n(y_i-f(x_i;\beta ){)}^2$$

其中 $\beta$ 是模型的参数，$f(x_i;\beta )$ 是模型对 $x_i$ 的预测值。优化问题的目标是使残差的平方和最小化，即使得模型预测值与观测值之间的误差尽可能小。

---

假设我们有一组观测数据 $(x_i,y_i)$，其中 $x_i$ 是自变量（特征），$y_i$ 是因变量（目标值）。我们希望找到一个线性模型 $y=mx+b$，其中 $m$ 是斜率，$b$​ 是截距，使得模型预测值与观测值之间的误差最小化。

以下为推理过程，实际上就是最小二乘法：

步骤1

首先，我们定义残差 $e_i$ 为观测值 $y_i$ 与模型预测值 $m{x}_i+b$ 之间的差异：
$$e_i=y_i-(m{x}_i+b)$$

我们的目标是使残差的平方和最小化，即求解下面的优化问题：

$$\underset{m,b}{\min }\sum _{i=1}^n{e}_i^2$$

其实也就是：
$$\underset{\beta }{\min }\sum _{i=1}^n(y_i-(m{x}_i+b){)}^2$$

步骤2

如何寻找函数的极值点？

1. 确定函数的定义域：首先，需要知道函数在哪个区间或集合上是定义的，因为极值点必须在函数的定义域内。

2. 求导：计算函数的一阶导数。这是因为在极值点处，函数的导数为零或导数不存在。一阶导数告诉我们函数在某点处的瞬时变化率。

3. 解方程找临界点：将一阶导数等于零，解这个方程找到所有可能的临界点。临界点是函数导数为零或导数不存在的点，函数在这些点可能有极值。

4. 二阶导数测试（如果需要）：为了确定这些临界点是否为极值点，可以使用二阶导数测试。如果某个临界点处的二阶导数大于零，则该点是局部最小值；如果二阶导数小于零，则该点是局部最大值；如果二阶导数等于零，则测试无法判定，可能需要进一步的分析。

5. 边界点检查：如果函数在闭区间上定义，还需要检查区间的端点，因为极值也可能出现在边界上。

6. 比较值：计算所有临界点和边界点处的函数值，以确定全局最大值和最小值（如果题目要求）。

通过这些步骤，就可以找到函数在其定义域内的所有局部极大值和极小值点，以及可能的全局极值点。

因为在极值点处，函数的导数为零或导数不存在，我们现在需要找到上述公式的极小值，也就是为了最小化这个目标函数，**（记住，此时我们需要将斜率m和截距b当作未知，因为这是我们需要求解的参数，我们要查看这两个值对于损失也就是残差的平方和的影响）**我们需要对 $m$ 和 $b$ 分别求偏导，并令偏导数等于零（因为这是一个二次函数，且定义域为实数集，所以通过求解其偏导数为零的点，即找到损失函数的极值点，从而得到最优的模型参数）。

对 $b$ 求偏导得到：
$$\frac{\partial }{\partial b}\sum _{i=1}^n{e}_i^2=-2\sum _{i=1}^n(y_i-(m{x}_i+b))=0$$

整理得到：

$$\sum _{i=1}^n(y_i-(m{x}_i+b))=0$$

进一步整理，我们得到：

$$\sum _{i=1}^n(y_i-m{x}_i-b)=0(1)$$

对 $m$ 求偏导得到：
$$\frac{\partial }{\partial m}\sum _{i=1}^n{e}_i^2=-2\sum _{i=1}^n{x}_i(y_i-(m{x}_i+b))=0$$

整理得到：

$$\sum _{i=1}^n(x_i{y}_i-m{x}_i^2-b{x}_i)=0(2)$$

步骤3

现在我们有(1)(2)两个方程，可以根据(1)和(2)得到如下的方程组：
$$\begin{array}{rl}\sum _{i=1}^n{x}_i{y}_i-m\sum _{i=1}^n{x}_i^2-b\sum _{i=1}^n{x}_i& =0\\ \sum _{i=1}^n{y}_i-m\sum _{i=1}^n{x}_i-nb& =0\end{array}$$
这是一个线性方程组，我们可以通过解这个方程组找到$a$和$b$的值。

为了求解 $m$，我们先从第二个方程开始，表达 $b$：
$$\begin{gathered} nb=\sum y_i-m\sum x_i \\ b=\frac{\sum y_i}{n}-m\frac{\sum x_i}{n} \\ b=\bar{y}-m\bar{x} \end{gathered}$$
其中，$\bar{x}$ 和 $\bar{y}$ 分别是 $x_i$ 和 $y_i$ 的均值。

接下来，将 $b$ 的表达式代入第一个方程中：
$$m\sum x_i^2+\left(\bar{y}-m\bar{x}\right)\sum x_i=\sum x_i{y}_i$$
这可以重新整理为：
$$m\sum x_i^2-m\bar{x}\sum x_i+\bar{y}\sum x_i=\sum x_i{y}_i$$
因为 $\sum x_i=n\bar{x}$，所以方程进一步简化为：
$$m\sum x_i^2-mn{\bar{x}}^2+n\bar{x}\bar{y}=\sum x_i{y}_i$$
然后，我们解 $m$：
$$\begin{gathered} m(\sum x_i^2-n{\bar{x}}^2)=\sum x_i{y}_i-n\bar{x}\bar{y} \\ m=\frac{\sum x_i{y}_i-n\bar{x}\bar{y}}{\sum x_i^2-n{\bar{x}}^2} \end{gathered}$$
因为如下两个式子等价：
$$\begin{gathered} \sum (x_i-\bar{x})(y_i-\bar{y}) \\ =\sum x_i{y}_i-\bar{y}\sum x_i-\bar{x}\sum y_i+n\bar{x}\bar{y} \\ =\sum x_i{y}_i-n\bar{x}\bar{y}-n\bar{x}\bar{y}+n\bar{x}\bar{y} \\ =\sum x_i{y}_i-n\bar{x}\bar{y} \end{gathered}$$
所以我们就相当于处理完了分子。现在我们再处理分母：
$$\begin{gathered} \sum (x_i-\bar{x}{)}^2 \\ =\sum (x_i^2-2\sum x_i\bar{x}+\sum {\bar{x}}^2) \\ =\sum x_i^2-2n\bar{x}+n{\bar{x}}^2 \\ =\sum x_i^2-n\bar{x} \end{gathered}$$
我们得到 $m$ 的最终表达式:
$$m=\frac{\sum (x_i-\bar{x})(y_i-\bar{y})}{\sum (x_i-\bar{x}{)}^2}$$
最后，我们使用 $m$ 的值回代到 $b$ 的表达式中得到 $b$：$b=\bar{y}-m\bar{x}$这样，我们就完成了 $m$ 和 $b$ 的求解过程。

3. 代码实现

根据以上思路，我们就可以写代码了。

题目描述：假设你是一位经济学家，正在研究家庭年收入（因变量 $Y$）与家庭主要收入者的教育年数（解释变量 $X$）之间的关系。你决定使用简单线性回归模型来分析这两个变量之间的关系。你收集了 10 个家庭的数据，如下所示：
[10, 12, 8, 15, 16, 18, 20, 14, 15, 11, 15, 19, 20]
[40, 45, 32, 50, 55, 65, 75, 48, 50, 38, 52, 70, 80]

1. 导入需要的库

import numpy as np
import matplotlib.pyplot as plt

2. 示例数据：教育年数(X)与家庭年收入(Y)的关系

——也就相当于题目给的数据集，然后题目要求我们找到他们之间的关系

X = np.array([10, 12, 8, 15, 16, 18, 20, 14, 15, 11, 15, 19, 20]).reshape(-1, 1)  # 教育年数
Y = np.array([40, 45, 32, 50, 55, 65, 75, 48, 50, 38, 52, 70, 80])  # 家庭年收入，单位：千美元

3. 绘制散点图看看数据长什么样先

# 绘制散点图
# 设置图的大小为长10，宽6
plt.figure(figsize=(8, 5), dpi=160)
plt.scatter(X, Y, color='black')
# 添加标题和坐标轴标签，中文显示会有问题，为了方便就用英文
plt.title('Education Years & Family Income')
plt.xlabel('Education Years')
plt.ylabel('Family Income')
plt.grid(True)
plt.show()

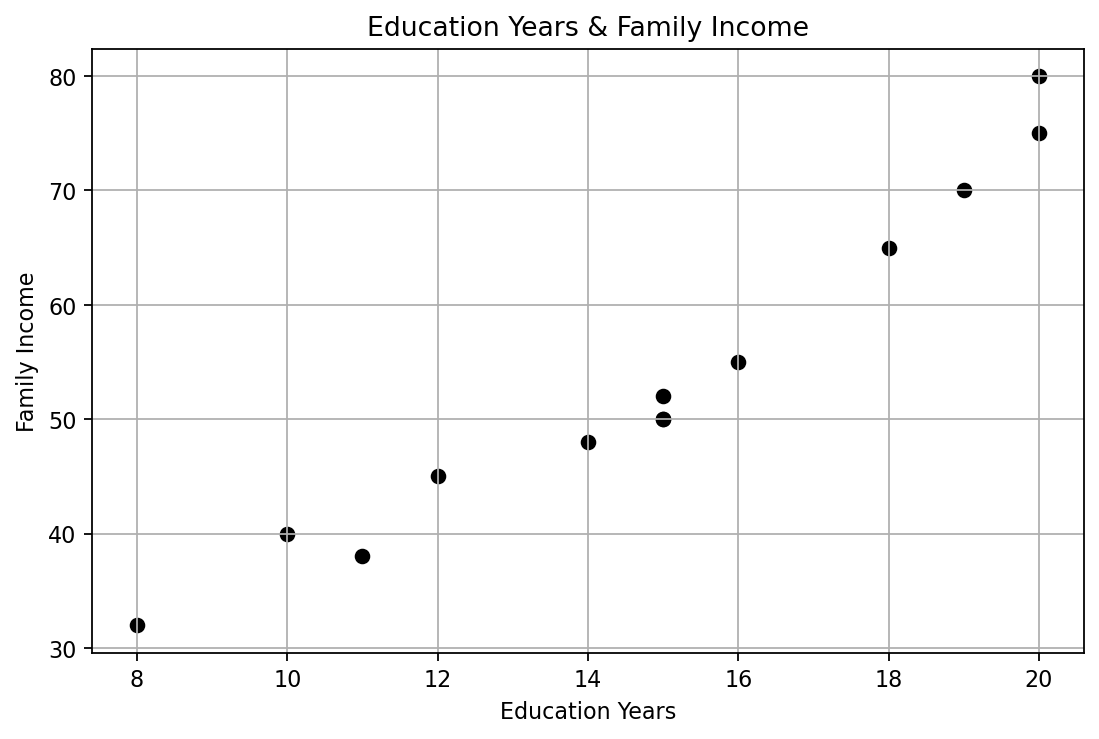
不使用scikit-learn库，手动实现简单线性回归，想一想如果想要用一条直线拟合这些点，我们需要计算些什么？

• 大家应该都很了解直线，需要一个斜率，需要一个截距
• 根据前面讲解的内容
  • 斜率的计算公式为：${\beta }_1=\frac{{\sum }_{i=1}^n(X_i-\bar{X})(Y_i-\bar{Y})}{{\sum }_{i=1}^n(X_i-\bar{X}{)}^2}$
  • 截距的计算公式为：${\beta }_0=\bar{Y}-{\beta }_1\bar{X}$
• 其中，$\bar{X}$和$\bar{Y}$分别为X和Y的均值
• 有了斜率和截距，我们就可以得到回归方程：$\hat{Y}={\beta }_0+{\beta }_{1}X$
• 有了回归方程，我们就可以预测Y值了

def simple_linear_regression(X, Y):
    # 计算X和Y的均值
    mean_X = np.mean(X)
    mean_Y = np.mean(Y)
    
    # 计算斜率(beta_1)和截距(beta_0)
    numerator = np.sum((X - mean_X) * (Y - mean_Y))
    denominator = np.sum((X - mean_X) ** 2)
    beta_1 = numerator / denominator # 斜率
    beta_0 = mean_Y - beta_1 * mean_X # 截距
    
    return beta_0, beta_1

4. 使用模型参数预测Y值

# 计算截距和斜率
beta_0, beta_1 = simple_linear_regression(X.flatten(), Y)

# 使用模型参数预测Y值
Y_pred_manual = beta_0 + beta_1 * X

5. 绘制回归线

# 绘制数据点和手动实现的回归线
plt.figure(figsize=(8, 5), dpi=160)
plt.scatter(X, Y, color='blue', label='Actual data')
plt.plot(X, Y_pred_manual, color='green', label='Manual Regression line')
plt.xlabel('Education Years')
plt.ylabel('Family Annual Income (k$)')
plt.title('Simple Linear Regression (Manual Implementation)')
plt.legend()
plt.show()

print('手动实现的回归方程为：Y = {:.2f} + {:.2f}X'.format(beta_0, beta_1))

手动实现的回归方程为：Y = -1.39 + 3.72X

6. 评估模型

# 计算R^2，也就是决定系数
# R^2 = SSR/SST
# SSR：回归平方和，SST：总平方和
# R^2的取值范围是0~1，越接近1，表明模型拟合的越好
SSR = np.sum((Y_pred_manual - np.mean(Y)) ** 2)  # 回归平方和
SST = np.sum((Y - np.mean(Y)) ** 2)  # 总平方和
R_square = SSR / SST
print('手动实现的R^2 = {:.4f}'.format(R_square))

手动实现的R^2 = 0.9414