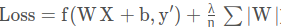Machine Vision Technology:Lecture2 Linear filtering
- Types of Images
- Image denoising图像去噪
- Defining convolution卷积的定义
- Key properties卷积的关键属性
- 卷积的其它属性
- Annoying details
- 卷积练习
- Sharpening锐化
- Gaussian Kernel
- Noise噪声 分类
- Gaussian noise高斯噪声
- Reducing salt-and-pepper noise:Median filtering中值滤波
- Sharpening revisited:再看锐化
- Edge detection | Origin of edges
- Characterzing edges描述边缘
- Image gradient图像梯度
计算机视觉(本科) 北京邮电大学 鲁鹏
Types of Images
二进制图像Binary:黑白图像。0表示Black,1表示White。
灰度图像Grayscale:每个像素用范围在0-255的灰度值表示。
彩色图像Color:RGB三通道。
Image denoising图像去噪
Moving average移动平均:一种通过使用过去若干时间段的平均值计算得出的平均值。移动平均值会定期变化,最早的数值会被基于最新数据的数值所替代。
- 用邻域的加权平均值替换每个像素
- 权重被称为滤波器核
filter kernel
一个3x3的权重为平均值的滤波核:

Defining convolution卷积的定义
Let f be the image and g be the kernel. The output of convolving fwith g is denoted f * g.
设
f
f
f 为图像,
g
g
g 为核,
f
f
f 和
g
g
g 的卷积输出定义为
f
∗
g
f*g
f∗g :
(
f
∗
g
)
[
m
,
n
]
=
∑
k
,
l
f
[
m
−
k
,
n
−
l
]
g
[
k
,
l
]
(f*g)[m,n] = \sum_{k,l}{f[m-k, n-l]g[k,l]}
(f∗g)[m,n]=k,l∑f[m−k,n−l]g[k,l]
对卷积进一步展开:
(
f
∗
g
)
[
m
,
n
]
=
∑
k
,
l
f
[
m
−
k
,
n
−
l
]
g
[
k
,
l
]
=
∑
k
=
−
1
k
=
1
∑
l
=
−
1
l
=
1
f
[
m
−
k
,
n
−
l
]
g
[
k
,
l
]
\begin{align} (f*g)[m,n] &= \sum_{k,l}{f[m-k, n-l]g[k,l]} \\ &= \sum_{k=-1}^{k=1} \sum_{l=-1}^{l=1} {f[m-k, n-l]g[k,l]} \end{align}
(f∗g)[m,n]=k,l∑f[m−k,n−l]g[k,l]=k=−1∑k=1l=−1∑l=1f[m−k,n−l]g[k,l]
假设有f为7x7,g为3x3的卷积核,此时k取-1、0、1,l取-1、0、1。
卷积示意图如下:

当m=2,n=2时:卷积操作如下
(
f
∗
g
)
[
2
,
2
]
=
∑
k
,
l
f
[
2
−
k
,
2
−
l
]
g
[
k
,
l
]
=
∑
k
=
−
1
k
=
1
∑
l
=
−
1
l
=
1
f
[
2
−
k
,
2
−
l
]
g
[
k
,
l
]
=
f
[
3
,
3
]
g
[
−
1
,
−
1
]
+
f
[
3
,
2
]
g
[
−
1
,
0
]
+
f
[
3
,
1
]
g
[
−
1
,
1
]
+
f
[
2
,
3
]
g
[
0
,
−
1
]
+
f
[
2
,
2
]
g
[
0
,
0
]
+
f
[
2
,
1
]
g
[
0
,
1
]
+
f
[
1
,
3
]
g
[
1
,
−
1
]
+
f
[
1
,
2
]
g
[
1
,
0
]
+
f
[
1
,
1
]
g
[
1
,
1
]
\begin{align} (f*g)[2,2] &= \sum_{k,l}{f[2-k, 2-l]g[k,l]} \\ &= \sum_{k=-1}^{k=1} \sum_{l=-1}^{l=1} {f[2-k, 2-l]g[k,l]} \\ &= f[3,3]g[-1,-1] + f[3,2]g[-1,0] + f[3,1]g[-1,1] \\ &+ f[2,3]g[0,-1] + f[2,2]g[0,0] + f[2,1]g[0,1] \\ &+ f[1,3]g[1,-1] + f[1,2]g[1,0] + f[1,1]g[1,1] \end{align}
(f∗g)[2,2]=k,l∑f[2−k,2−l]g[k,l]=k=−1∑k=1l=−1∑l=1f[2−k,2−l]g[k,l]=f[3,3]g[−1,−1]+f[3,2]g[−1,0]+f[3,1]g[−1,1]+f[2,3]g[0,−1]+f[2,2]g[0,0]+f[2,1]g[0,1]+f[1,3]g[1,−1]+f[1,2]g[1,0]+f[1,1]g[1,1]
示意图如下:

卷积核是翻转的:ppt中的图给成了镜像翻转,但上面推导怎么是旋转180度?

Key properties卷积的关键属性
- 线性性质Linearity: f i l t e r ( f 1 + f 2 ) = f i l t e r ( f 1 ) + f i l t e r ( f 2 ) filter(f_1 + f_2) = filter(f_1) + filter(f_2) filter(f1+f2)=filter(f1)+filter(f2)
- 平移不变性Shift invariance: f i l t e r ( s h i f t ( f ) ) = s h i f t ( f i l t e r ( f ) ) filter(shift(f)) = shift(filter(f)) filter(shift(f))=shift(filter(f))
- 理论结果Theoretical result:通过理论分析和计算得出的预测性结果:任何线性平移不变算子都可以表示为卷积
卷积的其它属性
-
交换律Commutative: a ∗ b = b ∗ a a * b = b * a a∗b=b∗a
从概念上讲,滤波器和信号没有区别
-
结合律Associative: a ∗ ( b ∗ c ) = ( a ∗ b ) ∗ c a*(b*c)=(a*b)*c a∗(b∗c)=(a∗b)∗c
-
分配律Distributes over addition: a ∗ ( b + c ) = a ∗ b + a ∗ c a*(b+c) = a*b + a*c a∗(b+c)=a∗b+a∗c
-
标量因子提出Scalars factor out: k a ∗ b = a ∗ k b = k ( a ∗ b ) ka*b = a*kb = k(a*b) ka∗b=a∗kb=k(a∗b)
-
同一性Identity:单位脉冲unit impulse e = [ . . . , 0 , 0 , 1 , 0 , 0 , . . . ] e = [..., 0,0,1,0,0,...] e=[...,0,0,1,0,0,...], a ∗ e = a a*e=a a∗e=a
Annoying details
卷积的输出结果与填充方式有关:在MATLAB中
filter2(g, f, shape)
shape='full':输出大小是f和g的和shape='same':输出大小和f相同shape='valid':输出大小是f和g的差

图像进行外推填充方式:
- clip filter (black): imfilter(f, g, 0) 周围补一圈黑色,像素为0的黑边
- wrap around: imfilter(f, g, ‘circular’) 图像右侧边缘补到左边,左侧边缘补到右边,类似圆筒,上下类似。
- copy edge: imfilter(f, g, ‘replicate’) 拉伸边缘像素
- reflect across edge: imfilter(f, g, ‘symmetric’) 镜像边缘像素
卷积练习

用右侧像素替代当前像素,相当于左移。

用box滤波器进行Blur模糊:

锐化滤波器Sharpening filter:突出和平均值的差异

Sharpening锐化

假设用 I I I 表示原图, e e e 表示单位脉冲,g表示box filter,上述过程表示如下:
原图减去滤波后的图: I ∗ e − I ∗ g = I ∗ ( e − g ) I*e - I*g = I*(e-g) I∗e−I∗g=I∗(e−g)
然后: I ∗ e + I ∗ ( e − g ) = I ∗ ( 2 e − g ) I*e + I*(e-g) = I*(2e - g) I∗e+I∗(e−g)=I∗(2e−g)
所以可以用新的滤波器 2 e − g 2e-g 2e−g 与原图进行卷积,直接得到sharpened图像。

Gaussian Kernel
为了消除边缘影响,根据邻近像素与中心的接近程度对其权重贡献。
G
σ
=
1
2
π
σ
2
e
−
(
x
2
+
y
2
)
2
σ
2
G_{\sigma} = \frac{1}{2 \pi \sigma^2} e^{- \frac{(x^2 + y^2)}{2 \sigma^2}}
Gσ=2πσ21e−2σ2(x2+y2)

5x5高斯模版生成过程:
- 中心坐标为(0,0),右边为(1,0),其余以此类推。
- 将坐标的x和y带入高斯函数得到值。
- 所有值还需要进行归一化(某个值除以所有值的和)。
模版的所有值加和为1,使模版操作不改变图像亮度。
- 标准偏差 σ \sigma σ 决定平滑程度
- 当固定模版的大小时:
σ \sigma σ 越小,模版的中间值越大,所占比重较大,被平滑的不那么厉害。
σ \sigma σ 越大,模版的中间值越小,所占权重变小,被平滑的厉害。

- 当 σ \sigma σ 固定时,模版大小改变:

当size为10时,模版有100个值,size为30时,模版有900个值,再归一化后,size小的模版权重相对更大些。
因此size较小时,被平滑的不那么厉害;size较大时,平滑的厉害。
- 模版大小选取遵循原则:将滤波器半宽度设置为约 3 σ 3\sigma 3σ。滤波器大小为 3 σ + 3 σ + 1 3\sigma + 3\sigma + 1 3σ+3σ+1。例如 σ = 1 \sigma=1 σ=1 时,滤波器大小为3x3
高斯滤波器特点:
-
从图像中去除“高频”成分(低通滤波器)
-
高斯滤波与自身的卷积是另一个高斯滤波器。
例如连续两个标准差为 σ \sigma σ 的高斯核进行卷积,等价于一个标准差为 2 σ \sqrt{2} \sigma 2σ 高斯核进行卷积。遵循勾股定理。
1.将原图进行参数为 σ \sigma σ 的高斯滤波: I ′ = I ∗ g σ I' = I * g_{\sigma} I′=I∗gσ
2.将上面结果进行参数为 σ \sigma σ 的高斯滤波: I ′ ′ = I ′ ∗ g σ I'' = I' * g_{\sigma} I′′=I′∗gσ
3.等价与直接将原图进行参数为 2 σ \sqrt{2} \sigma 2σ 的高斯滤波: I ′ ′ = I ∗ g 2 σ I'' = I * g_{\sqrt{2} \sigma} I′′=I∗g2σ
-
可分离核Separable Kernel:二维高斯函数可以被表示为两个一维高斯函数的乘积。
G σ ( x , y ) = 1 2 π σ 2 e − ( x 2 + y 2 ) 2 σ 2 = ( 1 2 π σ e − x 2 2 σ 2 ) ( 1 2 π σ e − y 2 2 σ 2 ) \begin{align} G_{\sigma}(x,y) &= \frac{1}{2 \pi \sigma^2} e^{- \frac{(x^2 + y^2)}{2 \sigma^2}} \\ &= (\frac{1}{2 \pi \sigma} e^{- \frac{x^2}{2 \sigma^2}})(\frac{1}{2 \pi \sigma} e^{- \frac{y^2}{2 \sigma^2}}) \\ \end{align} Gσ(x,y)=2πσ21e−2σ2(x2+y2)=(2πσ1e−2σ2x2)(2πσ1e−2σ2y2)
可分离性的例子:Separability example
首先使用2D高斯滤波器对中心位置进行卷积:求得结果是65。

2D高斯滤波器可以分解为两个一维高斯滤波器的乘积:

使用分解的两个一维高斯滤波器原原图像依次卷积:行卷积核列卷积。最终得到结果仍然是65.


Separability分离性的用途:
对 n × n n \times n n×n 的图像,使用 m × m m \times m m×m 的核进行卷积的复杂度: O ( n 2 m 2 ) O(n^2 m^2) O(n2m2)
如果使用分离的卷积的复杂度: O ( n 2 m ) + O ( n m ) = O ( n 2 m ) O(n^2 m) + O(n m) = O(n^2 m) O(n2m)+O(nm)=O(n2m)
Noise噪声 分类
- 椒盐噪声Salt and pepper noise:包含随机出现的黑色和白色像素。
- 脉冲噪声Impulse noise:包含随机出现的白色像素。
- 高斯噪声Gaussian noise:从高斯正态分布得出的强度变化

Gaussian noise高斯噪声
高斯噪声图
f
(
x
,
y
)
f(x,y)
f(x,y) 的产生如下:
f
(
x
,
y
)
=
f
ˉ
(
x
,
y
)
+
η
(
x
,
y
)
f(x, y) = \bar{f}(x, y) + \eta(x,y)
f(x,y)=fˉ(x,y)+η(x,y)
其中
f
ˉ
(
x
,
y
)
\bar{f}(x,y)
fˉ(x,y) 为理想的图像,
η
(
x
,
y
)
\eta(x,y)
η(x,y) 为噪声处理,所有噪声iid于正态分布:
η
(
x
,
y
)
∼
N
(
μ
,
σ
)
\eta(x,y) \sim \mathbf{N}(\mu, \sigma)
η(x,y)∼N(μ,σ)
假设:独立,均值为0的噪声

- 减少高斯噪声Reducing Gaussian noise:使用高斯滤波器

上图中第一行是 σ \sigma σ 取 0.05、0.1、0.2 产生的高斯噪声图。也就对应没有平滑的图。
第二行是使用 σ = 1 \sigma = 1 σ=1 的高斯滤波结果,此时高斯核大小为 7 × 7 7 \times 7 7×7。
第三行是使用 σ = 2 \sigma = 2 σ=2 的高斯滤波结果,此时高斯核大小为 13 × 13 13 \times 13 13×13。
结论:使用较大标准差的平滑可以抑制噪声, 但也会使图像模糊。
Reducing salt-and-pepper noise:Median filtering中值滤波
中值滤波器通过选择窗口中的中值强度对窗口进行操作。

中值滤波是非线性滤波。对异常值具有稳健性的优点:Robustness to outliers

下面是有椒盐噪声的图和均值滤波后的图:

Sharpening revisited:再看锐化

拉普拉斯高斯:

Edge detection | Origin of edges
- 边缘检测目标:识别图像中的突变(不连续)。直观地说,大多数来自图像的语义和形状信息都可以编码在边缘中。
各种边的起源(种类):边缘是由多种因素造成的

- surface normal discontinuity表面法向不连续:也就是面上的不连续,两个面的交界处产生的边。
- depth discontinuity间断面深度:深度上的边缘,上面瓶子因为是圆形的,本身没有边,但图像只能显示其中的一部分,由于深度上的不连续形成的边。
- surface color discontinuity表面颜色不连续:文字。
- illumination discontinuity照明不连续:阴影产生的边。
Characterzing edges描述边缘
边缘是图像强度函数中快速变化的地方:一阶导的极值点。

对于2D函数
f
(
x
,
y
)
f(x,y)
f(x,y) 的偏导数定义:
∂
f
(
x
,
y
)
∂
x
=
lim
ϵ
→
0
f
(
x
+
ϵ
,
y
)
−
f
(
x
,
y
)
ϵ
\frac{\partial f(x,y)}{\partial x} = \lim_{\epsilon \to 0} \frac{f(x + \epsilon,y) - f(x,y)}{\epsilon}
∂x∂f(x,y)=ϵ→0limϵf(x+ϵ,y)−f(x,y)
对于离散数据,我们可以使用有限差分进行近似:
∂
f
(
x
,
y
)
∂
x
≈
f
(
x
+
1
,
y
)
−
f
(
x
,
y
)
1
\frac{\partial f(x,y)}{\partial x} \approx \frac{f(x + 1,y) - f(x,y)}{1}
∂x∂f(x,y)≈1f(x+1,y)−f(x,y)
为了实现上面的卷积,相关的过滤器如何设计?

左图的滤波器: [ − 1 , 1 ] [-1,1] [−1,1] 。水平方向卷积,求得垂直方向边缘。
右图的滤波器: [ − 1 , 1 ] T [-1,1]^T [−1,1]T 或 [ 1 , − 1 ] T [1,-1]^T [1,−1]T 。垂直方向卷积,求得水平方向边缘。
Image gradient图像梯度
图像的梯度是由偏导数组成的向量:
∇
f
=
[
∂
f
∂
x
,
∂
f
∂
y
]
\nabla f = [\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}]
∇f=[∂x∂f,∂y∂f]
- 梯度方向指向信号变化最大的方向,也就是指向图像强度增加最快的方向。
- 梯度方向与边缘垂直。

梯度方向定义:
θ
=
t
a
n
−
1
(
∂
f
∂
y
/
∂
f
∂
x
)
\theta = tan^{-1} (\frac{\partial f}{\partial y} / \frac{\partial f}{\partial x})
θ=tan−1(∂y∂f/∂x∂f)
边缘强度由梯度幅度给出:The edge strength is given by the gradient magnitude
∣
∣
∇
f
∣
∣
=
(
∂
f
∂
x
)
2
+
(
∂
f
∂
y
)
2
|| \nabla f || = \sqrt{(\frac{\partial f}{\partial x})^2 + (\frac{\partial f}{\partial y})^2}
∣∣∇f∣∣=(∂x∂f)2+(∂y∂f)2
- 使用梯度幅值来描述是否是边的可能性,幅值越大,偏导数越大,偏导数越有可能是极值点,则该点越有可能是边。这也叫做边缘强度。









![SAP PO接口行项目json缺少中括号[]问题](https://img-blog.csdnimg.cn/direct/c8f9d4428b5345c1be2dffbde798d725.png)