Python算法题集_组合总和
- 题39:组合总和
- 1. 示例说明
- 2. 题目解析
- - 题意分解
- - 优化思路
- - 测量工具
- 3. 代码展开
- 1) 标准求解【值传递+回溯】
- 2) 改进版一【引用传递+堆栈回溯】
- 3) 改进版二【过程值列表缓存+遍历后检索】
- 4. 最优算法
- 5. 相关资源
本文为Python算法题集之一的代码示例
题39:组合总和
1. 示例说明
-
给你一个 无重复元素 的整数数组
candidates和一个目标整数target,找出candidates中可以使数字和为目标数target的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。candidates中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。对于给定的输入,保证和为
target的不同组合数少于150个。示例 1:
输入:candidates = [2,3,6,7], target = 7 输出:[[2,2,3],[7]] 解释: 2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选, 7 = 7 。 仅有这两种组合。示例 2:
输入: candidates = [2,3,5], target = 8 输出: [[2,2,2,2],[2,3,3],[3,5]]示例 3:
输入: candidates = [2], target = 1 输出: []提示:
1 <= candidates.length <= 302 <= candidates[i] <= 40candidates的所有元素 互不相同1 <= target <= 40
2. 题目解析
- 题意分解
- 本题是计算多个集合之间的求和问题,每个集合由若干个同样的整数组成
- 同样整数和不能超过target,所以多个集合都是有限集合,因此每个集合能合成出来的数值也是有限的,可以用回溯法求解
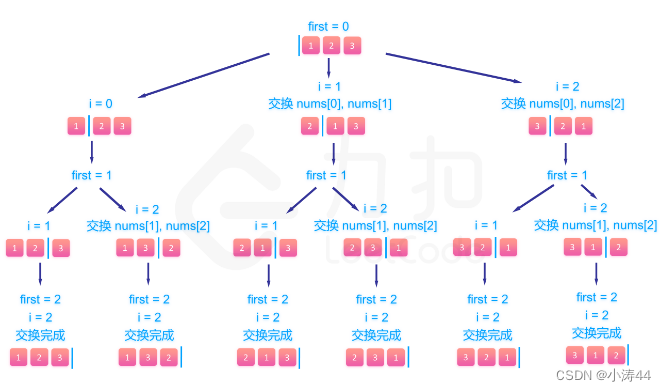
- 回溯法(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法。
- 优化思路
-
通常优化:减少循环层次
-
通常优化:增加分支,减少计算集
-
通常优化:采用内置算法来提升计算速度
-
分析题目特点,分析最优解
-
可以在回溯算法中使用值传递
-
可以在回溯算法中使用引用传递,但是应用传递必须解决回退操作,可以使用堆栈结构
-
可以考虑存储过程值列表,最后将等于target的集合返回
-
- 测量工具
- 本地化测试说明:LeetCode网站测试运行时数据波动很大【可把页面视为功能测试】,因此需要本地化测试解决数据波动问题
CheckFuncPerf(本地化函数用时和内存占用测试模块)已上传到CSDN,地址:Python算法题集_检测函数用时和内存占用的模块- 本题本地化超时测试用例自己生成,详见章节【最优算法】,代码文件包含在【相关资源】中
3. 代码展开
1) 标准求解【值传递+回溯】
使用列表作为值传递参数,逐层递归,完成回溯
页面功能测试,马马虎虎,超过40%
import CheckFuncPerf as cfp
class Solution:
def combinationSum_base(self, candidates, target):
def bracktracing(candidates, begin, ilen, path, ret, target):
if target < 0:
return
if target == 0:
ret.append(path)
return
for iIdx in range(begin, ilen):
bracktracing(candidates, iIdx, ilen, path + [candidates[iIdx]], ret,
target - candidates[iIdx])
ilen = len(candidates)
path, result = [], []
if ilen == 0:
return result
bracktracing(candidates, 0, ilen, path, result, target)
return result
aSolution = Solution()
result = cfp.getTimeMemoryStr(aSolution.combinationSum_base, nums, target)
print(result['msg'], '执行结果 = {}'.format(len(result['result'])))
# 运行结果
函数 combinationSum_base 的运行时间为 1076.25 ms;内存使用量为 12060.00 KB 执行结果 = 62271
2) 改进版一【引用传递+堆栈回溯】
使用列表作为引用传递参数,逐层递归,完成回溯
页面功能测试,马马虎虎,超越71%
import CheckFuncPerf as cfp
class Solution:
def combinationSum_ext1(self, candidates, target):
candidates.sort()
path, result = [], []
idx, isum = 0, 0
def bracktracing(idx, isum, path):
if sum(path) == target:
result.append(path[:])
return
for jIdx in range(idx, len(candidates)):
if isum + candidates[jIdx] > target:
return
path.append(candidates[jIdx])
isum += candidates[jIdx]
bracktracing(jIdx, isum, path)
path.pop()
isum -= candidates[jIdx]
bracktracing(idx, isum, path)
return result
aSolution = Solution()
result = cfp.getTimeMemoryStr(aSolution.combinationSum_base, nums, target)
print(result['msg'], '执行结果 = {}'.format(len(result['result'])))
# 运行结果
函数 combinationSum_base 的运行时间为 1076.25 ms;内存使用量为 12060.00 KB 执行结果 = 62271
3) 改进版二【过程值列表缓存+遍历后检索】
使用多维列表结构保存各数值对应的组合列表,遍历完成后下标检索对应组合列表
页面功能测试,马马虎虎,超过23%
import CheckFuncPerf as cfp
class Solution:
def combinationSum_ext2(self, candidates, target):
import copy
candidates.sort()
dp = [[] for x in range(target + 1)]
for candidate in candidates:
for iIdx in range(candidate, target + 1):
if candidate == iIdx:
dp[iIdx].append([candidate])
else:
for combination in dp[iIdx - candidate]:
tmpgroup = copy.deepcopy(combination)
tmpgroup.append(candidate)
dp[iIdx].append(tmpgroup)
return dp[target]
aSolution = Solution()
result = cfp.getTimeMemoryStr(aSolution.combinationSum_base, nums, target)
print(result['msg'], '执行结果 = {}'.format(len(result['result'])))
# 运行结果
函数 combinationSum_base 的运行时间为 1076.25 ms;内存使用量为 12060.00 KB 执行结果 = 62271
4. 最优算法
根据本地日志分析,最优算法为第1种方式【值传递+回溯】combinationSum_base
本题测试数据,似乎能推出以下结论:
- 组合的回溯求解中,值传递性能优于引用传递的堆栈结构
- 内存对象过多后,性能下降明显,如
combinationSum_ext2
nums = [x for x in range(10, 20)]
target = 200
aSolution = Solution()
result = cfp.getTimeMemoryStr(aSolution.combinationSum_base, nums, target)
print(result['msg'], '执行结果 = {}'.format(len(result['result'])))
result = cfp.getTimeMemoryStr(aSolution.combinationSum_ext1, nums, target)
print(result['msg'], '执行结果 = {}'.format(len(result['result'])))
result = cfp.getTimeMemoryStr(aSolution.combinationSum_ext2, nums, target)
print(result['msg'], '执行结果 = {}'.format(len(result['result'])))
# 算法本地速度实测比较
函数 combinationSum_base 的运行时间为 1076.25 ms;内存使用量为 12060.00 KB 执行结果 = 62271
函数 combinationSum_ext1 的运行时间为 1243.29 ms;内存使用量为 11848.00 KB 执行结果 = 62271
函数 combinationSum_ext2 的运行时间为 14627.27 ms;内存使用量为 16080.00 KB 执行结果 = 62271
5. 相关资源
本文代码已上传到CSDN,地址:Python算法题源代码_LeetCode(力扣)_组合总和
一日练,一日功,一日不练十日空
may the odds be ever in your favor ~