机试指南：Ch5:线性数据结构 Ch6:递归与分治

news2025/2/24 6:58:20

文章目录

  • 第5章 线性数据结构
    • 1.向量 vector
    • 2.队列 queue
      • (1)队列的特点、应用
      • (2)基本操作
      • (3)例题
        • 例题1：约瑟夫问题2 （难度：中等）
      • (4)习题
        • 习题1：排队打饭 （难度：中等）
    • 3.栈 stack
      • (1)栈的特点、应用
      • (2)基本操作
      • (3)例题
        • 例题1：编排字符串 （难度：简单）
        • 例题2：括号匹配 （难度：中等）
        • 例题3：计算表达式 （难度：困难）
      • (4)习题
        • 习题1：堆栈的使用 （难度：简单）
        • 习题2：模拟出入栈游戏 （难度：中等）
        • 习题3：简单计算器 （难度：困难）
  • 第6章 递归与分治
    • 1.递归
      • (1)原理
        • ①函数
        • ②递归
      • (2)例题
        • 例题1：n的阶乘 （难度：入门）
        • 例题2：汉诺塔Ⅲ （难度：简单）【分治法-递归】
    • 2.分治
      • (1)原理
      • (2)例题
        • 例题1：跳台阶 （难度：简单)
        • 例题2：不连续1的子串（难度：中等）
        • 例题3：2的幂次方（难度：困难）
      • (3)习题
        • 习题1：Fibonacci （难度：入门）
        • 习题2：二叉树 （难度：简单）【递归】
        • 习题3：骨牌铺地砖 （难度：简单） 【动态规划】
        • 习题4：矩阵幂 （难度：中等） 【矩阵计算】
        • 习题5：全排列 （难度：困难）【递归回溯法 - DFS】

第5章 线性数据结构

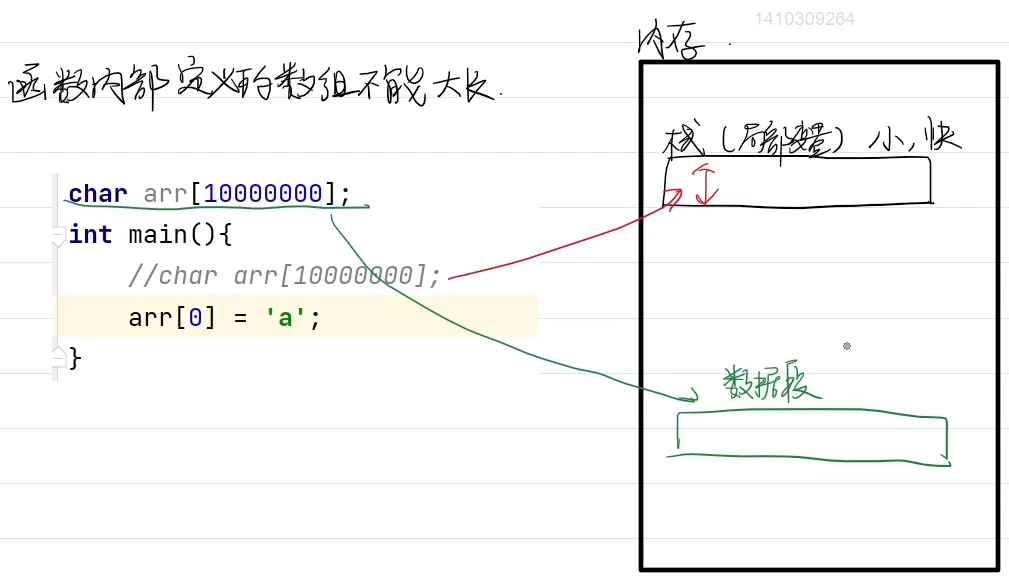
1.当定义的数组特别大，达到1千万时，不能定义在函数内部，会崩溃。栈比较小，但快。
要定义在全局位置，数据段中。
【局部大数组会崩溃，全局大数组不会崩溃】
在这里插入图片描述

2.标准模板库STL


1.向量 vector

vector是动态数组，长度可改变。 vector<int> vec;//创建空向量，长度为0
普通静态数组长度是固定不变的。int arr[100];//创建长度为100的静态数组

1.头文件

#include <vector>
using namespace std;

2.声明向量

vector<int> vec;//长度为0

3.赋初值

vector<int> vec2 = {1,2,3};

4.申请一定空间的向量，所有元素初值默认为0

vector<int> vec3(10000);

※5.尾部插入：尾部扩容 push_back(元素) 。效率最高，插入n个为O(n)，插入1个为O(1)。

vec.push_back(1);//vec[0]=1
vec.push_back(3);//vec[1]=3

※6.任意位置插入：

vec.insert(pos,[个数,]内容);

//头部插入字符串
vec.insert(vec.begin(),str);

※7.尾部删除：弹出尾部元素 pop_back()

vec.pop_back();

※8.下标访问

vec[i] //下标>=n时，数组越界

9.长度计算

vec.size();

10.两种遍历方法
①下标遍历

for(unsigned int i = 0; i < vec.size(); ++i){
	printf("vec[%d] = %d\n",i,vec[i]);
}

②迭代器遍历

for(vector<int>::iterator it = vec.begin(); it != vec.end(); ++it){
	printf("vec[] = %d\n",*it);
}

11.随机位置的插入：insert(位置，元素)

vector<int>::iterator it1 = vec.begin()+1;//迭代器指针指向vector的第二个位置
vec.insert(it1，3);//在vector第二个位置插入元素3

12.随机位置的删除：erase(位置);

vec.erase(vec.begin());//删除vector的第一个位置的元素

13.vector的实现原理
(1)vector的组成、申请空间(堆上)
vector是类类型，包括size容量、capacity内存大小、ptr首地址
首地址存放在栈上，但vector申请的内存空间在堆区上，堆区比栈区大，因此vector可申请空间比静态数组在栈上申请的空间可以大很多。【静态数组 - 栈 - 小空间。 vector - 堆- 大空间】

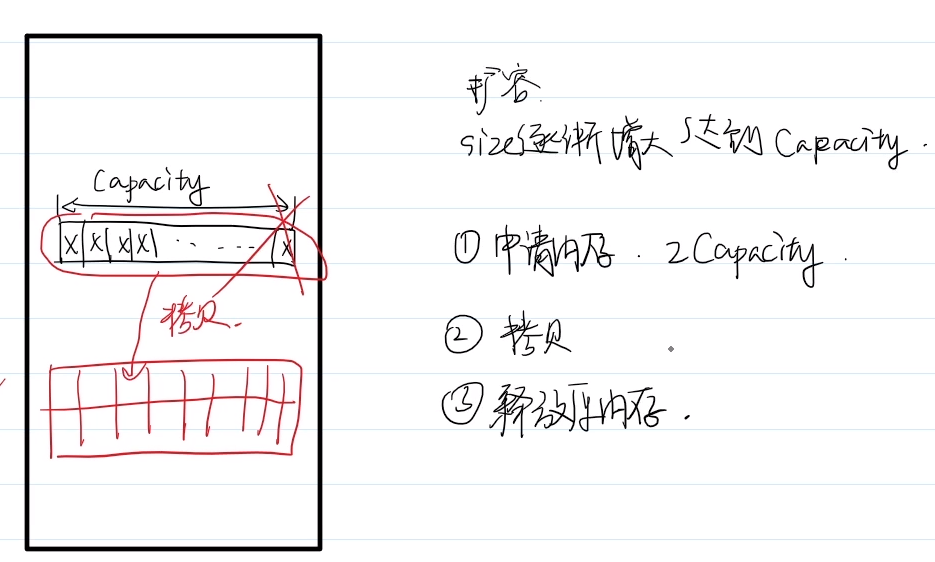
(2)vector的扩容机制
在这里插入图片描述



2.队列 queue

(1)队列的特点、应用

1.队列的特点
队列queue是受限制的线性表
先进先出，FIFO
队尾入队，队头出队。

2.队列应用：
广度优先遍历 BFS


(2)基本操作

0.头文件

#include <queue>
using namespace std;

queue<int> myQueue;

1.队尾入队 .push(变量名)

for(int i = 0;i <= 5;++i){
	myQueue.push(i);
}

2.队头出队 .pop()
3.判空 .empty()
4.队首元素 .front()
5.队尾元素 .back()

#include <iostream>
#include <queue>
using namespace std;

int main() {
    //队列初始化
    queue<int> myQueue;
    //判空
    if(myQueue.empty()){
        cout << "myQueue is empty!" << endl;
    }
    //队尾入队
    for(int i = 0 ; i < 10; ++i){
        myQueue.push(i);
        //打印队首、队尾
        cout << "队首:" << myQueue.front() << "  队尾:" << myQueue.back() << endl;
    }
    cout << "---------------" << endl;
    //队首出队
    for(int i = 0 ; i < 9; ++i){
        myQueue.pop();
        //打印队首、队尾
        cout << "队首:" << myQueue.front() << "  队尾:" << myQueue.back() << endl;
    }
    return 0;
}

(3)例题

例题1：约瑟夫问题2 （难度：中等）

提交网址：http://bailian.openjudge.cn/practice/3254

在这里插入图片描述
在这里插入图片描述

思路：队头元素插入队尾，然后队头元素出队，以此实现循环队列

#include <iostream>
#include <queue>
using namespace std;

int main() {
    queue<int> myQueue;
    int n,p,m;
    while(cin >> n >> p >> m){
        if(n==0 && p==0 && m==0)  break;
        //初始化队列
        for(int i = 1; i <= n; ++i){
            myQueue.push(i);
        }
        //将编号为p旋转到队头
        for(int i = 1; i < p; ++i) {  //将1到p-1号元素从队头调整到队尾
            myQueue.push(myQueue.front()); //队头元素插入队尾
            myQueue.pop(); //队头出队
        }
        //开始计数过程
        while(!myQueue.empty()){
            //将m-1个元素从队头调整到队尾
            for(int i = 1; i < m; ++i){
                myQueue.push(myQueue.front());
                myQueue.pop();
            }
            //打印并移除第m个元素
            cout << myQueue.front();
            if(myQueue.size() > 1) cout << ",";
            myQueue.pop();
        }
        cout << endl;
    }
    return 0;
}

(4)习题

习题1：排队打饭 （难度：中等）

提交网址：https://www.acwing.com/problem/content/description/5063/

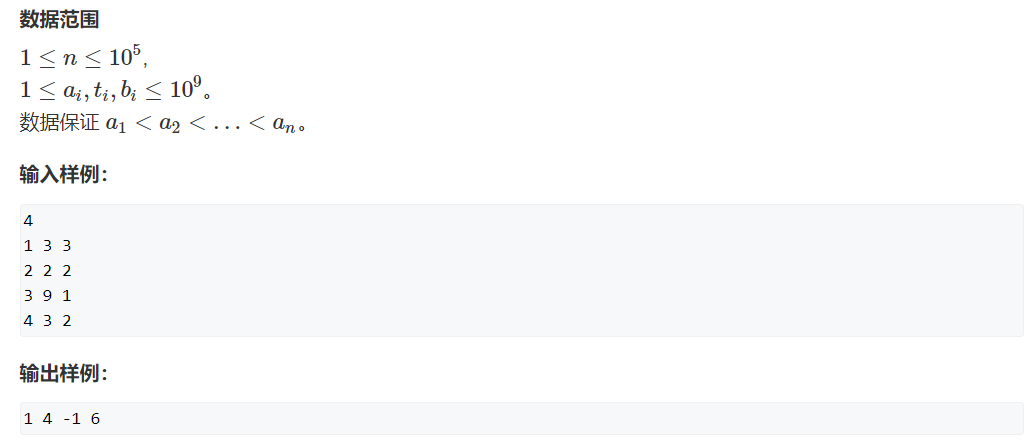
在这里插入图片描述
在这里插入图片描述

几个注意事项：
①可能前面有连续几个没打上饭的，得用int记录而不是bool
②有些数值超过了int的表示范围，将数组由int类型改为long long

#include <iostream>
using namespace std;

int main() {
    int n;
    long long a[100010],t[100010],b[100010],res[100010]; //a[i]为到达时刻,t[i]为打饭耗时,b[i]为最大等待时长,res[i]为打饭时刻或-1
    cin >> n;
    for(int i = 1; i <= n; ++i){
        cin >> a[i] >> t[i] >> b[i];
    }
    res[1] = a[1];  //第一位同学到达后立即开始打饭
    cout << res[1] <<" ";
    int count = 0; //count记录前面有连续多少位同学没有打上饭
    for(int i = 2; i <= n; ++i){
        if(a[i]+b[i] < res[i-1-count]+t[i-1-count]){ //上一位开始打饭时间+打饭耗时超过了该同学最大等待时间,则放弃打饭
            cout << "-1 ";
            count++;
        }else{
            res[i] = max(res[i-1-count]+t[i-1-count],a[i]); //max(最早可以打饭时刻,该同学到达时间)
            cout << res[i] << " ";
            count = 0;
        }
    }
    cout << endl;
    return 0;
}



3.栈 stack

(1)栈的特点、应用

1.栈的特点
栈也是操作受限的线性表，只能一端进出。
后进先出
栈，禁止操作的一端称为盲端。允许元素插入和删除的一端称为栈顶。

2.栈的应用
①深度优先遍历 DFS：逆序输出
②表达式解析、表达式求值
③递归
④括号匹配


(2)基本操作

0.头文件

#include <stack>
using namespace std;

1.初始化

stack<typename> myStack//定义

2.方法
.push()：压栈，将元素加入栈中
.pop()：弹栈
.top()：获取栈顶内容
.size()：栈大小
.empty()：判断栈是否为空

#include <iostream>
#include <stack>
using namespace std;

int main() {
    //栈初始化
    stack<int> myStack;
    //栈判空
    if(myStack.empty()){
        cout << "myStack is empty!" << endl;
    }
    //入栈(压栈)
    for(int i = 0; i < 10 ; ++i){
        myStack.push(i);
        cout << "top is " << myStack.top() << endl;
    }
    cout << "---------------" <<endl;
    //出栈(弹栈)
    for(int i = 0 ; i < 9; ++i){
        myStack.pop();
        cout << "top is " << myStack.top() << endl;
    }
    return 0;
}

(3)例题

例题1：编排字符串 （难度：简单）

提交网址：https://www.acwing.com/problem/content/3578/
在这里插入图片描述
在这里插入图片描述

思路：准备一个临时栈，用于演示弹栈

#include <iostream>
#include <stack>
#include <string>
using namespace std;

int main() {
    string str;
    stack<string> myStack,tempStack;
    int m;
    cin >> m;
    for(int i = 0; i < m; ++i){
        cin >> str;
        myStack.push(str);
        tempStack = myStack;
        for(int i = 1; !tempStack.empty(); ++i){
            if(i > 4) break;  //最多输出4个字符串
            cout << i << "=" << tempStack.top() << " ";
            tempStack.pop();
        }
        cout << endl;
    }
    return 0;
}

例题2：括号匹配 （难度：中等）

提交网址：https://www.acwing.com/problem/content/3696/

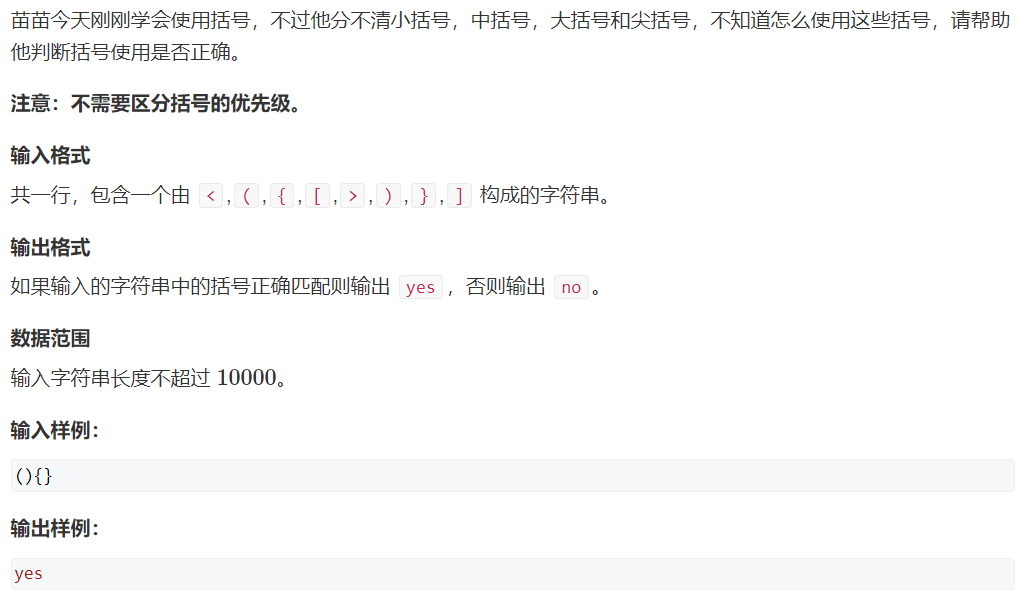
在这里插入图片描述


思路：栈实现。遇到右括号都是同一种思路，写好一个else if，后面都是复制了

#include <iostream>
#include <string>
#include <stack>
using namespace std;

int main() {
    stack<char> myStack;
    string str;
    cin >> str;
    for(int i = 0; i < str.size(); ++i){
        //1.遇到左括号,入栈
        if(str[i] == '<' || str[i] == '(' || str[i] == '[' || str[i] == '{'){
            myStack.push(str[i]);
        }
        //2.遇到右尖括号
        else if(str[i] == '>'){
            if(myStack.empty() || myStack.top()!='<'){
                cout << "no" << endl;
                return 0;
            }else{  //栈顶就是左尖括号,匹配
                myStack.pop();
            }
        }
        //3.遇到右小括号
        else if(str[i] == ')'){
            if(myStack.empty() || myStack.top()!='('){
                cout << "no" << endl;
                return 0;
            }else{  //栈顶就是左小括号,匹配
                myStack.pop();
            }
        }
        //4.遇到右中括号
        else if(str[i] == ']'){
            if(myStack.empty() || myStack.top()!='['){
                cout << "no" << endl;
                return 0;
            }else{  //栈顶就是左中括号,匹配
                myStack.pop();
            }
        }
        //5.遇到右大括号
        else if(str[i] == '}'){
            if(myStack.empty() || myStack.top()!='{'){
                cout << "no" << endl;
                return 0;
            }else{  //栈顶就是左大括号,匹配
                myStack.pop();
            }
        }
    }
    if(myStack.empty())    cout << "yes" << endl;
    else                   cout << "no"  << endl;
    return 0;
}

例题3：计算表达式 （难度：困难）

提交网址：http://t.cn/AiKKJjJ5
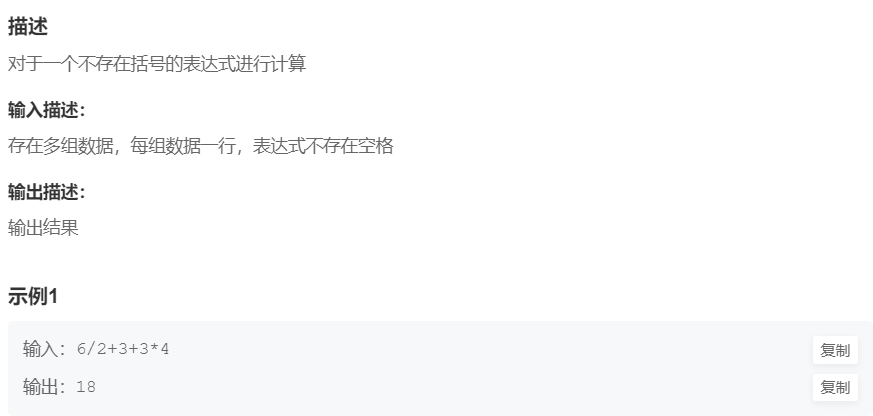
在这里插入图片描述

#include <stdio.h>
#include <string>
#include <stack>
#include <map>
using namespace std;
int main() {
    char str[1000] = { 0 };
    map<char, int> priority = {
        {'\0',0},
        {'+',1},{'-',1},
        {'*',2},{'/',2}
    };
    while (scanf("%s", str) != EOF) {
        string numStr = "";
        stack<char> opStack;
        stack<double> numStack;
        for (int i = 0; ; ++i) {
            if (str[i] >= '0' && str[i] <= '9') {
                numStr.push_back(str[i]);
            }
            else {
                double num = stod(numStr);
                numStr = "";
                numStack.push(num);
                // 什么时候弹栈？ 栈非空 && 新op的优先级 不高于 栈顶的优先级
                // 循环弹栈和计算
                while (!opStack.empty() &&
                    priority[str[i]] <= priority[opStack.top()]) {
                    double rhs = numStack.top();
                    numStack.pop();
                    double lhs = numStack.top();
                    numStack.pop();
                    char curOp = opStack.top();
                    opStack.pop();

                    if (curOp == '+') {
                        numStack.push(lhs + rhs);
                    }
                    else if (curOp == '-') {
                        numStack.push(lhs - rhs);
                    }
                    else if (curOp == '*') {
                        numStack.push(lhs * rhs);
                    }
                    else if (curOp == '/') {
                        numStack.push(lhs / rhs);
                    }
                }
                // 栈为空 或者 新op的优先级高于栈顶
                if (str[i] == '\0') {
                    printf("%d\n", (int)numStack.top());
                    break;
                }
                else {
                    opStack.push(str[i]);
                }
            }
        }
    }
    return 0;
}

(4)习题

习题1：堆栈的使用 （难度：简单）

提交网址：http://t.cn/AiKKM6F6
在这里插入图片描述
在这里插入图片描述

#include <iostream>
#include <stack>
using namespace std;

int main() {
    int n;
    while(cin >> n){
        stack<int> myStack;
        char c;
        int a;
        for(int i = 0; i < n; ++i){
            cin >> c;
            if(c == 'A'){
                if(myStack.empty()) cout << "E" << endl;
                else                cout << myStack.top() << endl;
            }else if(c == 'P'){
                cin >> a;
                myStack.push(a);
            }else if(c == 'O'){
                if(!myStack.empty())    myStack.pop();
            }
        }
    }
    return 0;
}

习题2：模拟出入栈游戏 （难度：中等）

提交网址：https://www.acwing.com/problem/content/3681/

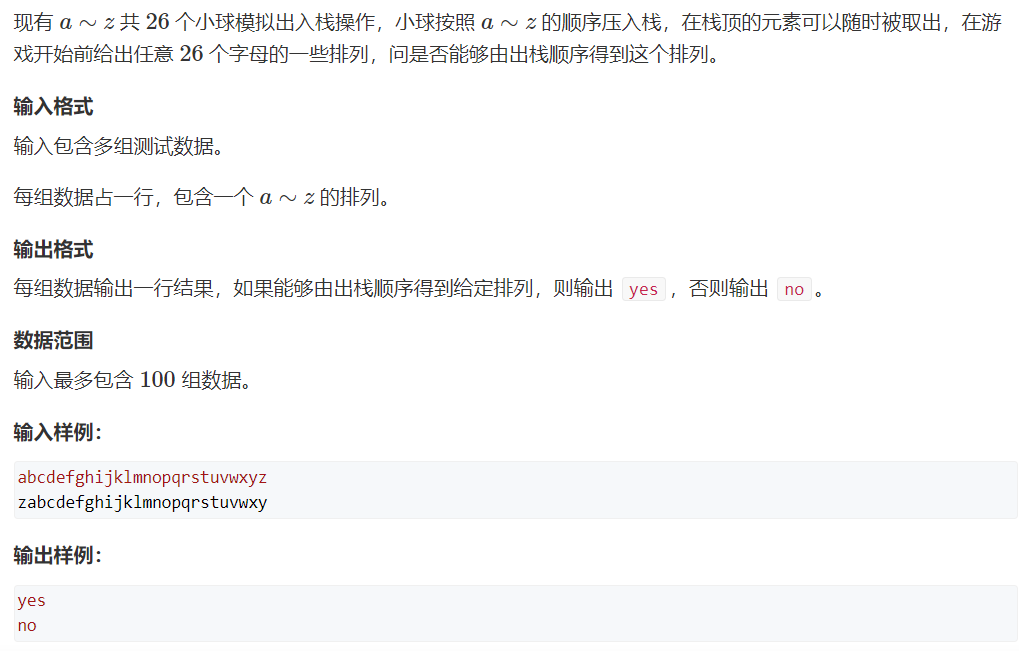
在这里插入图片描述

注意，栈的初始化放在while循环里。放在外面可能会因为上一轮未清空，受脏数据影响

#include <iostream>
#include <stack>
#include <string>
using namespace std;

int main() {
    string str1 = "abcdefghijklmnopqrstuvwxyz",str2;
    while(cin >> str2){
        stack<char> stk;
        int k = 0;
        for(int i = 0 ; i < str1.size(); ++i){
            stk.push(str1[i]);
            while(stk.size() && k < str2.size() && stk.top() == str2[k]){//核心while循环:
                stk.pop();                            //比较栈顶元素和字符串str2中当前位置的字符是否相等
                k++;
            }
        }
        if(stk.empty())  cout << "yes" << endl;
        else             cout << "no"  << endl;
    }
    return 0;
}

习题3：简单计算器 （难度：困难）

提交网址：http://t.cn/AiKoGS94

在这里插入图片描述



第6章 递归与分治

1.递归

(1)原理

1.什么是递归？
函数在函数体内调用自身函数的行为叫做递归
（在函数定义中调用本函数，叫做递归）


2.递归的原理：
①代码段：PC走到被调函数的入口
②栈区：栈帧压入栈内

逐过程、逐语句

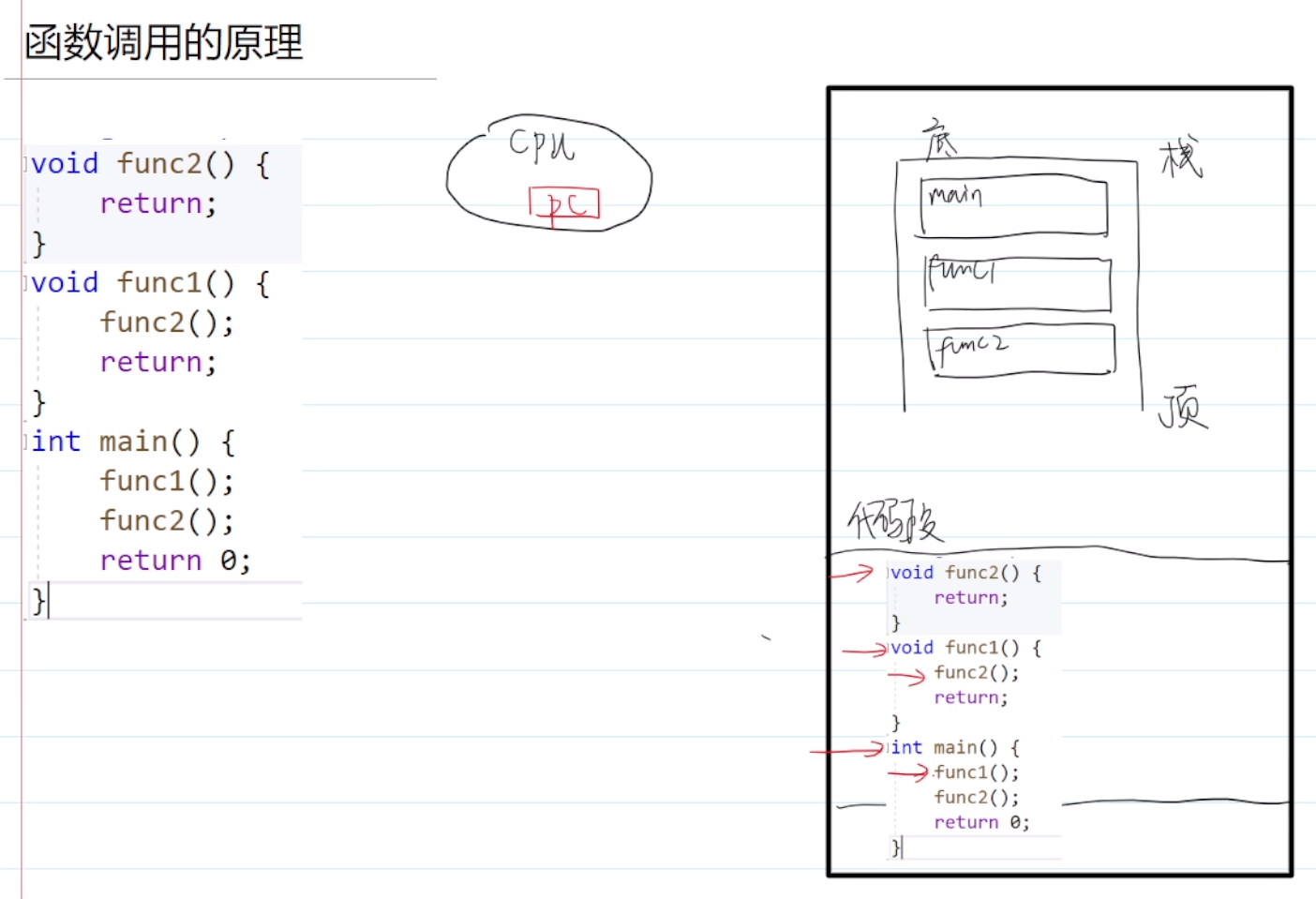
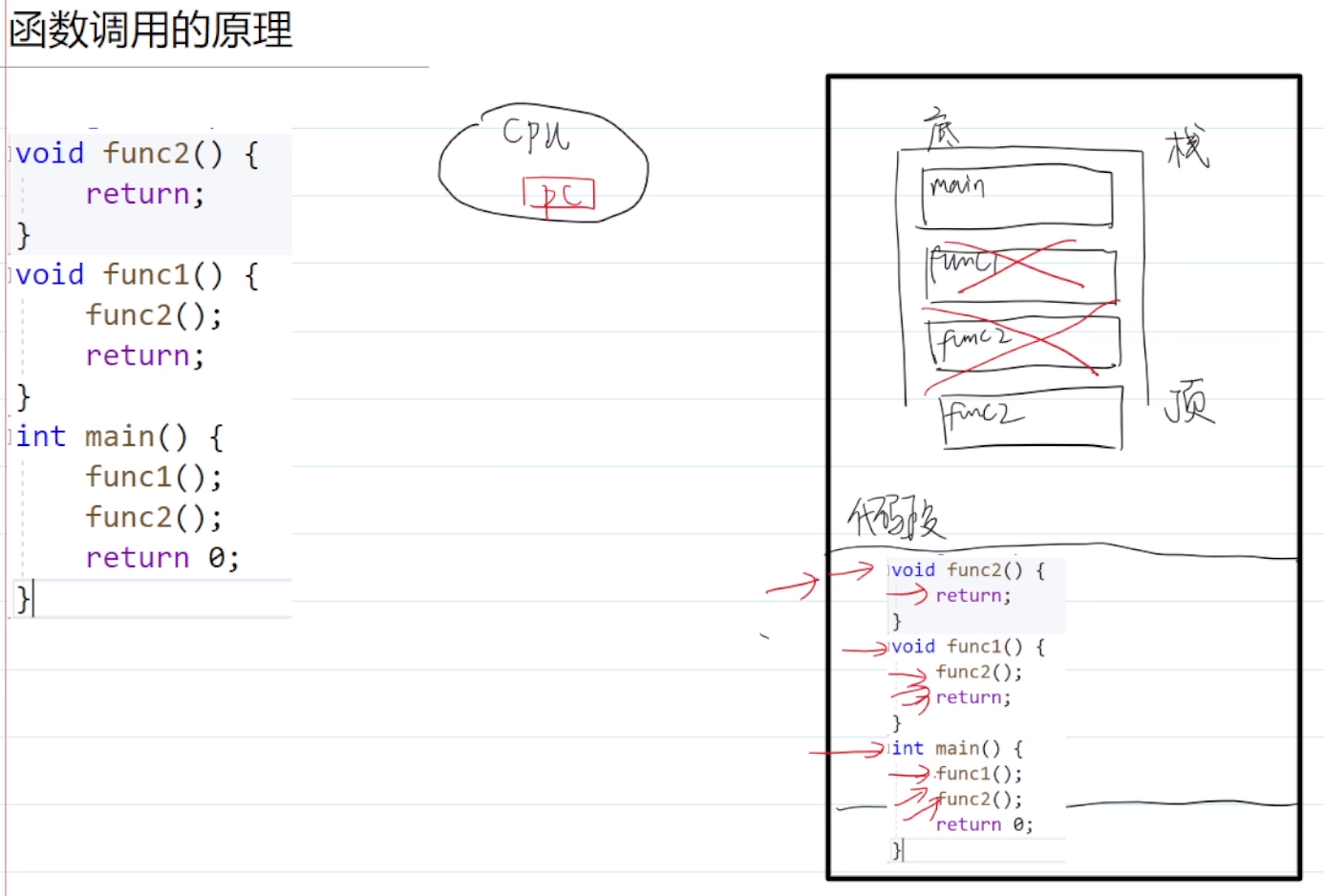
在这里插入图片描述
在这里插入图片描述


3.如何使用递归？
①递归一定要有递归出口
②每次递归，变量条件向着递归出口靠近


4.递归与分治的关系：
分治是一种思想，分而治之；递归是一种实现方法，函数调用自己。
分治思想可用递归来实现，也可以用其他方法来实现。递归作为一种方法，不止可以用于实现递归思想，也可以用来实现其他思想。
但总的来说，一般都用递归方法来实现分治的思想。故两者本不是同一纬度的概念，但是经常放在一起谈论。

常见的分治：求斐波那契数列、快速排序
常见的递归：求n的阶乘


5.2023旧版本内容：
从函数到递归

①大问题→小问题，等价条件
②确定最小问题，即递归出口

①函数

C语言编写的代码，以函数定义为单位。

call：把PC移到被调函数
ret：把PC移回主调函数


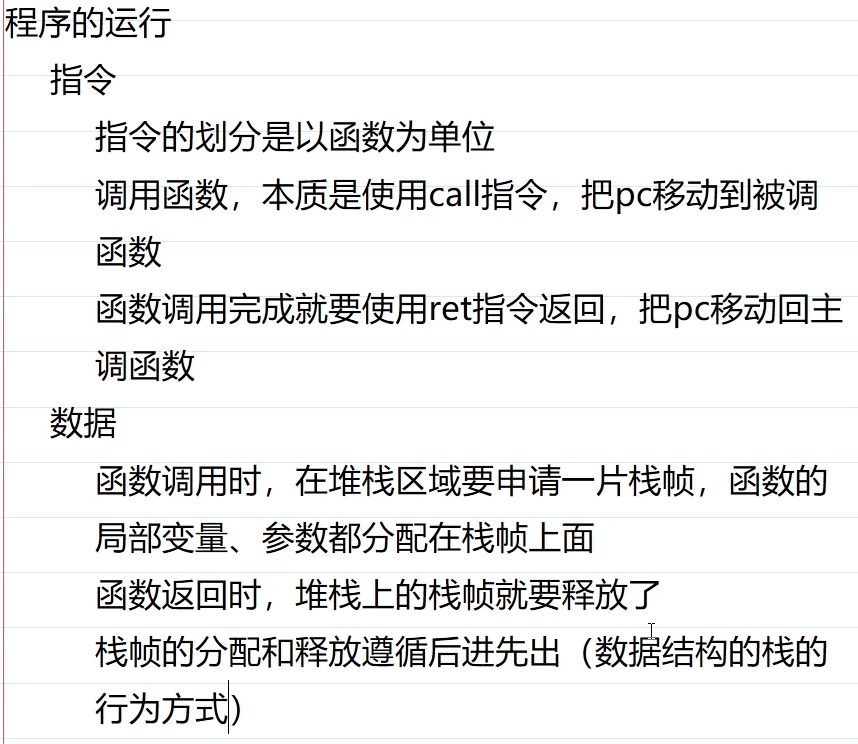
②递归

递归关注的两个点：
①大问题转化为小问题：规模n→规模n-1
②最小问题：递归出口


(2)例题

例题1：n的阶乘 （难度：入门）

提交网址：https://www.nowcoder.com/share/jump/2891302591709206218373

在这里插入图片描述

C++：

#include <iostream>
using namespace std;

long long factorial(int n){
    if(n == 0 || n == 1)    return n;
    else{
        return n * factorial(n-1);
    }
}

int main(){
    int n;
    cin >> n;
    cout << factorial(n);
    return 0;
}

C语言：

#include <cstdio>

long long int Factorial(int n){
    if(n == 0){
        return 1;
    }else{
        return n*Factorial(n-1);
    }
}

int main(){
    int n;
    while(scanf("%d",&n) != EOF){
        printf("%lld",Factorial(n));
    }
    return 0;
}

例题2：汉诺塔Ⅲ （难度：简单）【分治法-递归】

在这里插入图片描述
在这里插入图片描述

思路：
①n-1片为整体，先由第一柱搬到第三柱，最大片由第一柱搬到第二柱；[Hanoi(n-1) + 1]
②n-1片从第三柱搬回第一柱，最大片由第二柱搬到第三柱； [Hanoi(n-1) + 1]
③n-1片由第一柱搬到第三柱，完成。[Hanoi(n-1)]

#include <iostream>
using namespace std;

long long Hanoi(int n){ //搬运n片共需要Hanoi(n)步
    if(n == 1){
        return 2; 
    }else{
        return 3 * Hanoi(n-1) + 2; 
    }
}

int main() {
    int n;
    while(cin >> n){
        cout << Hanoi(n) << endl;
    }
    return 0;
}



2.分治

(1)原理

1.名称解释
分治法，分而治之 (divide-and-conquer method)


2.分治法的两个要素
①大问题转化为相似的小问题，直至转化为最小问题
②最小问题的解决方案

在这里插入图片描述


3.分治法的代码模板
①分解：大问题拆成小问题
②治理：找到等价条件，解决递归出口(最小问题)
③合并

在这里插入图片描述


(2)例题

例题1：跳台阶 （难度：简单)

提交网址：https://www.acwing.com/problem/content/823/

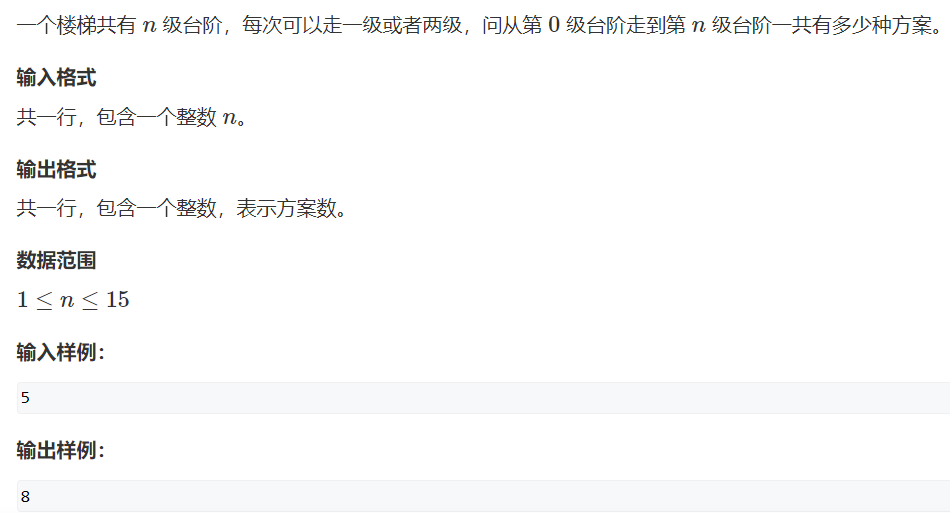
在这里插入图片描述


思路：因为每次只能走1级或2级台阶，所以走n级台阶只会是从n-1或n-2级台阶上去的。根据加法原理，这两种方案的数量可以相加得到走n级台阶的方案。同样的，走n-1级的方案可以拆分为走n-2级和走n-3级方案之和。

在这里插入图片描述

#include <iostream>
using namespace std;

int f(int n){
    if(n == 1){
        return 1;
    }else if(n == 2){
        return 2;
    }else{
        return f(n-1) + f(n-2);
    }
}

int main() {
    int n; //n级台阶
    while(cin >> n){
        cout << f(n) << endl;
    }
    return 0;
}

测试可得：
f(1)=1，f(2)=2，f(3)=3，f(4)=5，f(5)=8，f(6)=13，f(7)=21 …
可知，跳台阶问题是斐波那契数列问题的变形，即后一个值是前两个值之和。


优化分析：
但是由栈帧示意图，我们发现很多f(n)会重复计算多次。当n很大时，该算法的效率会很低。我们自然而然地想到如何避免重复计算从而提高函数的效率。
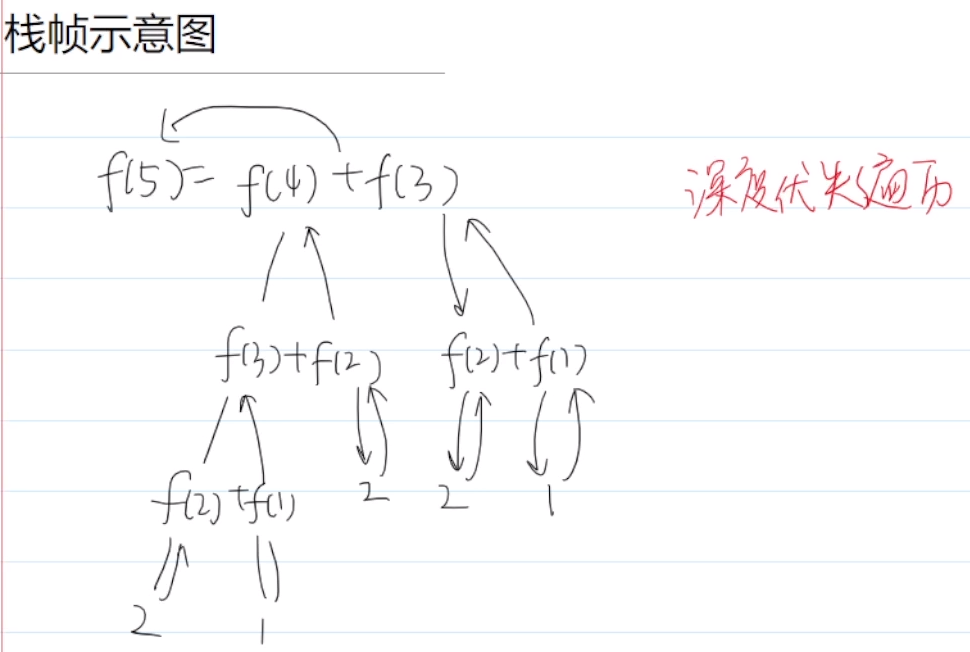
在这里插入图片描述

优化:用数组存储已经计算过的结果

例题2：不连续1的子串（难度：中等）

提交网址：https://www.acwing.com/problem/content/3709/

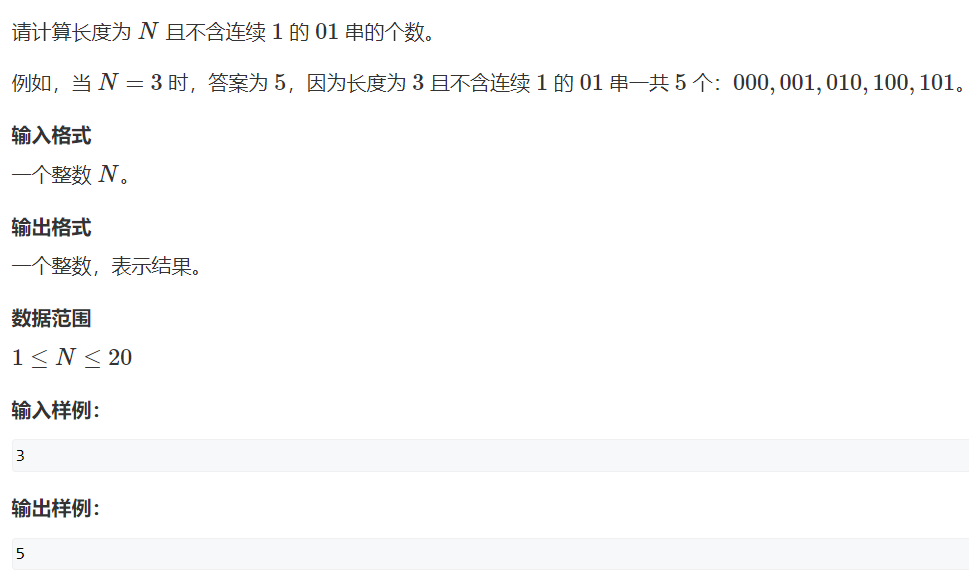
在这里插入图片描述


24炉灰老师：分解为小问题，并给出最小问题的解决方案(递归出口)

#include <iostream>
using namespace std;

int f0(int n); // 函数声明写在前面,
int f1(int n); // 则这两个函数就可以交叉调用

int f0(int n){ // 末尾为0
    if(n == 1){
        return 1;
    }else{
       return f0(n-1) + f1(n-1);
    };
}

int f1(int n){ // 末尾为1
    if(n == 1){
        return 1;
    }else{
        return f0(n-1);
    }
}

int main() {
    int n;
    while(cin >> n){
        cout << f0(n)+f1(n) << endl;
    }
    return 0;
}

例题3：2的幂次方（难度：困难）

提交网址：https://www.acwing.com/problem/content/3486/

在这里插入图片描述


分析：由大问题分解为小问题，用分治法

在这里插入图片描述


将n转化为2的指数形式：
在这里插入图片描述


24炉灰老师

#include <stdio.h>
#include <string>
#include <vector>
using namespace std;
string Get2sExponet(int n) {
    if (n == 0) {
        return "0";
    }
    vector<int> exp;
    for (int i = 15; i >= 0; --i) {
        if ((n & (1 << i)) != 0) {
            exp.push_back(i);
        }
    }
    // n = 2^(exp[0]) + 2^(exp[1]) + ... + 2^(exp[size-1])
    string res = "";
    for (int i = 0; i < exp.size(); ++i) {
        if (i != 0) {
            res += "+";
        }
        if (exp[i] == 1) {
            res += "2";
        }
        else {
            res += "2(" + Get2sExponet(exp[i]) + ")";
        }
    }
    return res;
}
int main() {
    int n;
    while (scanf("%d", &n) != EOF) {
        printf("%s\n", Get2sExponet(n).c_str());
    }
    return 0;
}



(3)习题

习题1：Fibonacci （难度：入门）

提交网址：http://t.cn/Ai0K3tU5

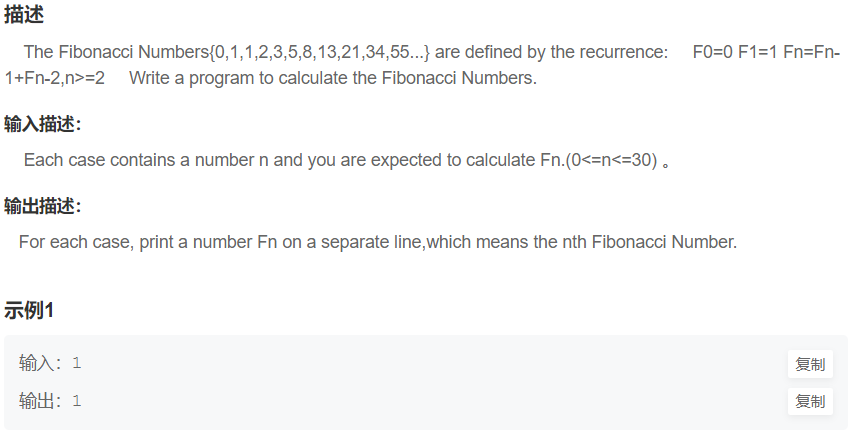
在这里插入图片描述

解法1：斐波那契数列，递归实现
C语言版本：

#include <cstdio>

int Fibonacci(int n ){
    if(n == 0 || n == 1){
        return n;
    }else{
        return Fibonacci(n-1) + Fibonacci(n-2);
    }
}

int main(){
    int n;
    while(scanf("%d",&n) != EOF){
        printf("%d\n",Fibonacci(n));
    }
    return 0;
}

C++版本：

#include <iostream>
using namespace std;

int Fibonacci(int n){
    if(n == 0 || n == 1){
        return n;
    }else{
        return Fibonacci(n-1) + Fibonacci(n-2);
    }
}

int main(){
    int n;
    while(cin >> n){
        cout << Fibonacci(n);
    }
    return 0;
}

解法2：斐波那契数列（非递归实现，循环实现）

#include <cstdio>

int fib(int n){
    int n1 = 1;
    int n2 = 1;
    int ret = 0;
    if (n==1 || n==2){
        return 1;
    }
    for (int i = 3; i <= n; i++){ //通过循环计算n>=3时
        ret = n1 + n2;
        n1 = n2;
        n2 = ret;
    }
    return ret;
}

int main(){
    int n = 0;
    scanf("%d", &n);
    int ret = fib(n);
    printf("%d\n",ret);
    return 0;
}

解法3：斐波那契数列（非递归实现，动态规划实现）

#include <cstdio>

int dp[91];

int Fibonacci(int n){
    dp[1] = 1;
    dp[2] = 2;
    for(int i = 3 ; i <= n; ++i){ //3-n
        dp[i] = dp[i-1] + dp[i-2];
    }
    return dp[n];
}

int main(){
    int n;
    while(scanf("%d",&n) != EOF){
        printf("%d\n",Fibonacci(n));
    }
    return 0;
}

习题2：二叉树 （难度：简单）【递归】

提交网址：http://t.cn/Ai0Ke6I0
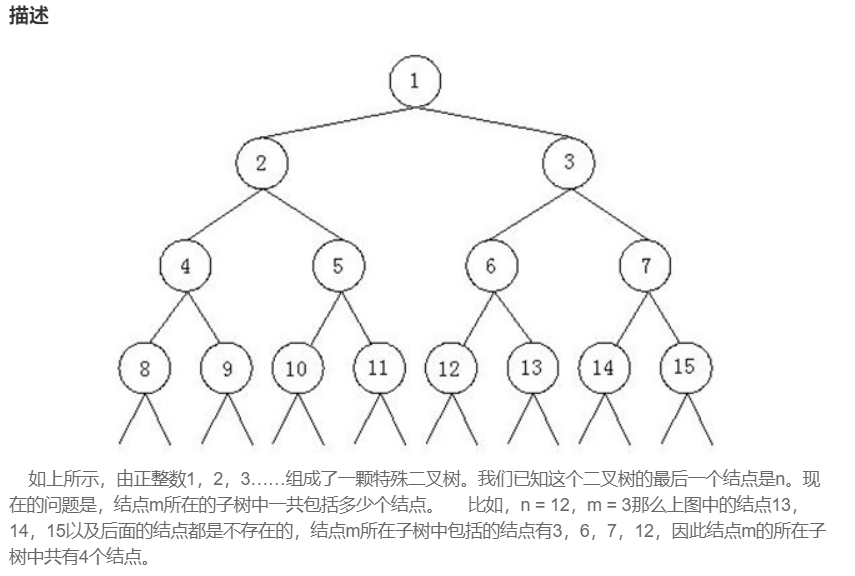
在这里插入图片描述
在这里插入图片描述

C++版本：根结点 + 左子树 + 右子树
如图，编号为m的结点，左孩子编号为2m，右孩子编号为2m+1

#include <iostream>
using namespace std;

int binarytree(int m,int n){
     if(m > n){
        return 0;
     }else{         //如图,编号为m的结点,左孩子编号为2m，右孩子编号为2m+1
        return 1 + binarytree(2*m,n) + binarytree(2*m+1,n); //根结点 + 左子树 + 右子树
     }
}

int main(){
    int m,n; //m为父结点编号,n为总结点数
    while(cin >> m >> n){
        if(m==0 && n==0) break;
        cout << binarytree(m,n) << endl;
    }
    return 0;
}

C语言版本：

#include <cstdio>

int binaryTree(int m,int n){
    if(m>n){
        return 0;
    }else{
        return binaryTree(2*m,n) + binaryTree(2*m+1,n) + 1;
    }
}

int main(){
    int m,n;
    while(scanf("%d %d",&m,&n) != EOF){
        if(m<=0 && n<=0){
            break;
        }
        printf("%d\n",binaryTree(m,n));
    }
}

习题3：骨牌铺地砖 （难度：简单） 【动态规划】

提交网址：https://www.acwing.com/problem/content/3690/

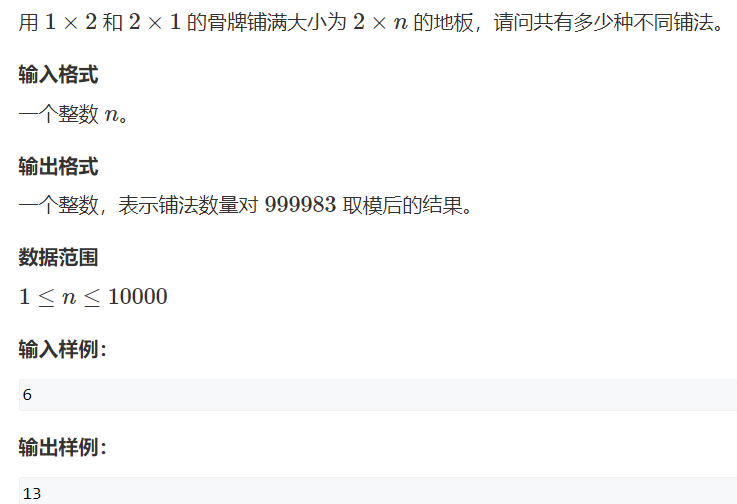
在这里插入图片描述

思路：
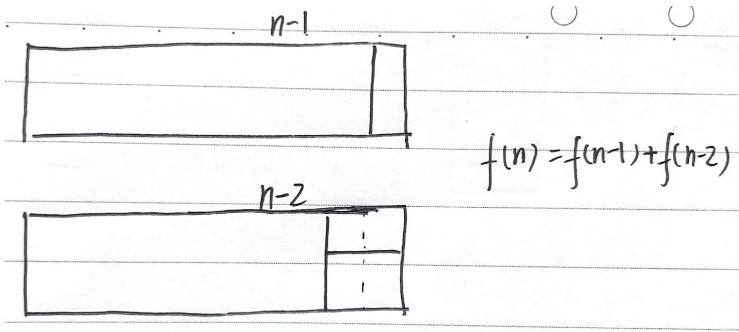
在这里插入图片描述

用递归会超时，改用动态规划，数组保存计算结果，避免重复计算

#include <iostream>
using namespace std;

int dp[10010];

long long Fibonacci(int n){
	dp[0] = 0;
    dp[1] = 1;
    dp[2] = 2;
    for(int i = 3; i <= n; ++i){
        dp[i] = (dp[i-1] + dp[i-2]) % 999983;
    }
    return dp[n];
}

int main() {
    int n;
    cin >> n;
    cout << Fibonacci(n);
    return 0;
}

习题4：矩阵幂 （难度：中等） 【矩阵计算】

提交网址：https://www.acwing.com/problem/content/3690/

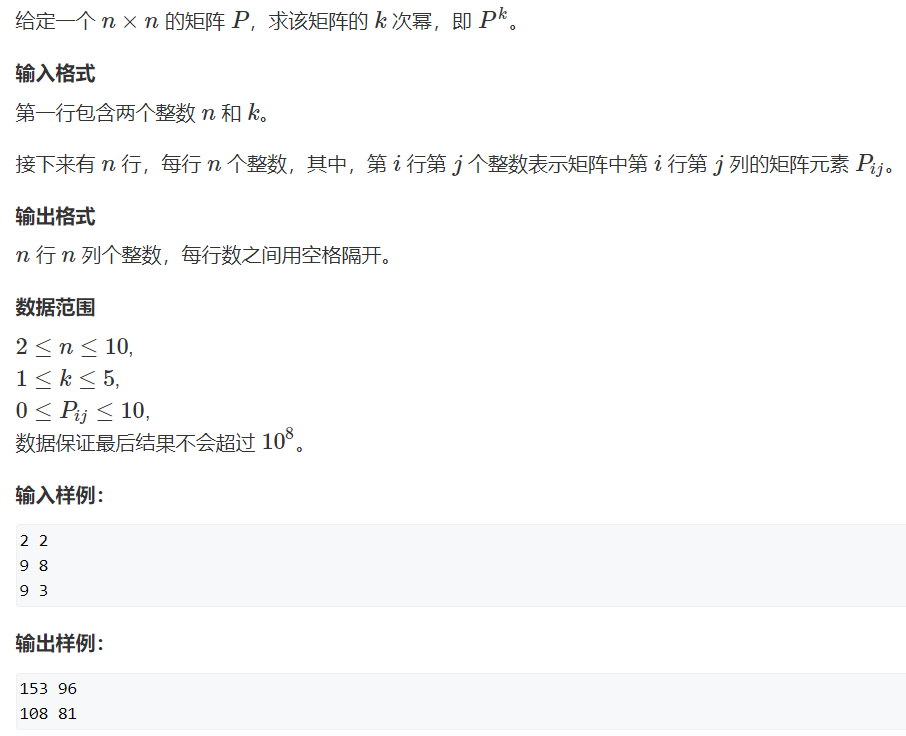
在这里插入图片描述

学会计算 矩阵C = A×B
核心代码：

for(int i = 0; i < n; ++i){
    for(int j = 0; j < n; ++j){
        for(int k = 0; k < n; ++k){      //矩阵C = 矩阵A × 矩阵B:
            C[i][j] += A[i][k]*B[k][j]; //C[i][j] = A的第i行×B的第j列所有对应元素
        }
    }
}

答案：

#include <iostream>
#include <cstring>
using namespace std;
const int N = 11;
int A[N][N],B[N][N],C[N][N];

int main() {
    int n,m; //n为矩阵的阶,m为矩阵的幂
    cin >> n >> m;
    memset(A,0,sizeof(A));
    //输入矩阵A
    for(int i = 0; i < n; ++i){
        for(int j = 0; j < n; ++j){
            cin >> A[i][j];
        }
    }
    //计算m次幂
    //(1)若m为1,输出原矩阵
    if(m == 1){
        for(int i = 0; i < n; ++i){
            for(int j = 0; j < n; ++j){
                cout << A[i][j] << " ";
            }
            cout << endl;
        }
        return 0;
    }
    //(2)若m>1,计算 矩阵 C = A×B
    memcpy(B,A,sizeof(A));
    while(--m){
        memset(C,0,sizeof(C));
        for(int i = 0; i < n; ++i){
            for(int j = 0; j < n; ++j){
                for(int k = 0; k < n; ++k){      //矩阵C = 矩阵A × 矩阵B:
                    C[i][j] += A[i][k]*B[k][j]; //C[i][j] = A的第i行×B的第j列所有对应元素
                }
            }
        }
        memcpy(B,C,sizeof(C)); //这次的幂次运算结果C赋值给B
    }
    //输出矩阵C
    for(int i = 0; i < n; ++i){
        for(int j = 0; j < n; ++j){
            cout << C[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

习题5：全排列 （难度：困难）【递归回溯法 - DFS】

提交网址：https://www.acwing.com/problem/content/3690/

在这里插入图片描述

来自一位网友的答案：

#include<bits/stdc++.h>
using namespace std;
void backtracking(string tmp,string s)
{
    if(tmp.size()==s.size())
        cout<<tmp<<endl;
    else
    {
        for(int i=0;i<s.size();++i)
        {
            if(tmp.find(s[i])!=tmp.npos) continue;
            backtracking(tmp+s[i],s);
        }
    }
}
int main()
{
    string s,tmp=""; 
    while(cin>>s)
        backtracking(tmp,s);   
    return 0;
 }

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1477960.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

jsjiami.v7关于js加密运行环境的探索

jsjiami.v7关于js加密运行环境的探索

浏览器环境、Node.js 环境和 vm2 环境之间存在一些区别&#xff0c;包括全局对象、核心模块和一些环境特定的 API。下面是一些区别的简要概述&#xff0c;以及一些代码示例来突显它们之间的不同。 1. 浏览器环境&#xff1a; 全局对象&#xff1a; 浏览器环境&#xff1a; 全…
阅读更多...
加速AI测试领域的进化，顶尖专家与名校教授强强联合，助你快速成为人工智能测试领域的精英

加速AI测试领域的进化，顶尖专家与名校教授强强联合，助你快速成为人工智能测试领域的精英

随着人工智能在各行各业的广泛应用&#xff0c;学习并掌握AI技术在软件测试中的应用变得至关重要。不仅能使你跟上行业的发展趋势&#xff0c;还能提升你的竞争力。而且&#xff0c;市场对具备AI测试技能的测试工程师的需求正日益增长&#xff0c;这使得掌握这些技能能够帮助你…
阅读更多...
Linux网络编程(四-TCP协议)

Linux网络编程(四-TCP协议)

目录 一、TCP概念 二、TCP的首部格式 三、TCP可靠传输机制 3.1 确认应答机制 3.2 超时重传机制 3.3 连接管理 3.3.1 三次握手 3.3.2 四次挥手 3.4 流量控制 3.5 拥塞控制 四、TCP效率机制 4.1 滑动窗口 4.2 重发控制 4.3 延迟应答 4.4 捎带应答 五、TCP的…
阅读更多...
【Linux C | 网络编程】gethostbyname 函数详解及C语言例子

【Linux C | 网络编程】gethostbyname 函数详解及C语言例子

&#x1f601;博客主页&#x1f601;&#xff1a;&#x1f680;https://blog.csdn.net/wkd_007&#x1f680; &#x1f911;博客内容&#x1f911;&#xff1a;&#x1f36d;嵌入式开发、Linux、C语言、C、数据结构、音视频&#x1f36d; &#x1f923;本文内容&#x1f923;&a…
阅读更多...
【Java程序设计】【C00323】基于Springboot的高校科研信息管理系统（有论文）

【Java程序设计】【C00323】基于Springboot的高校科研信息管理系统（有论文）

基于Springboot的高校科研信息管理系统&#xff08;有论文&#xff09; 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于Springboot的高校科研信息管理系统&#xff0c;本系统有管理员、学校管理员、科研人员三种角色&#xff1b; 管理员&#xff1a;首页、个…
阅读更多...
企业数字化转型的第一步：由被动多云向主动多云转变

企业数字化转型的第一步：由被动多云向主动多云转变

随着经济环境、市场形势、技术发展、用户需求等诸多因素的变化&#xff0c;数字化转型为企业进一步提升效率和竞争力、提供更加丰富的个性化产品和服务、进行业务场景创新、探寻新的增长机会和运营模式提供了崭新的途径。越来越多的企业意识到&#xff0c;数字化转型已不是企业…
阅读更多...
数据仓库与数据挖掘概述

数据仓库与数据挖掘概述

目录 一、数据仓库概述 &#xff08;一&#xff09;从传统数据库到数据仓库 &#xff08;二&#xff09;数据仓库的4个特征 &#xff08;三&#xff09;数据仓库系统 &#xff08;四&#xff09;数据仓库系统体系结构 &#xff08;五&#xff09;数据仓库数据的粒度与组织…
阅读更多...
机器人内部传感器阅读梳理及心得-速度传感器-数字式速度传感器

机器人内部传感器阅读梳理及心得-速度传感器-数字式速度传感器

在机器人控制系统中&#xff0c;增量式编码器既可以作为位置传感器测量关节相对位置&#xff0c;又可作为速度传感器测量关节速度。当作为速度传感器时&#xff0c;既可以在模拟量方式下使用&#xff0c;又可以在数字量方式下使用。 模拟式方法 在这种方式下&#xff0c;需要…
阅读更多...
day02_前后端环境搭建(前端工程搭建,登录功能说明,后端项目搭建)

day02_前后端环境搭建(前端工程搭建,登录功能说明,后端项目搭建)

文章目录 1. 软件开发介绍1.1 软件开发流程1.2 角色分工1.3 软件环境1.4 系统的分类 2. 尚品甄选项目介绍2.1 电商基本概念2.1.1 电商简介2.1.2 电商模式B2BB2CB2B2CC2BC2CO2O 2.2 业务功能介绍2.3 系统架构介绍2.4 前后端分离开发 3. 前端工程搭建3.1 Element-Admin简介3.2 El…
阅读更多...
django框架不调试下会被达出史(sql查询次数，消耗时间)

django框架不调试下会被达出史(sql查询次数，消耗时间)

1:使用pycharm编辑器里面 2:安装django-debug-toolbar 3:进行调试查询 https django框架调试,各个面板查询消耗时间&#xff0c;pycharm,debug 1&#xff1a;settings.py INSTALLED_APPS列表中添加 INSTALLED_APPS [# 使用多合一有点慢# multi_captcha_admin,# 多合一验证码i…
阅读更多...
Git安装的一些步骤解说（小白好奇心严重版本）

Git安装的一些步骤解说（小白好奇心严重版本）

Use bundled OpenSSH 安装 Git 时&#xff0c;您面临的选择是使用 Git 自带的 SSH 客户端&#xff08;bundled OpenSSH&#xff09;还是使用系统上已安装的外部 SSH 客户端&#xff08;external OpenSSH&#xff09;。以下是两个选项的一些考虑因素&#xff1a; 使用 Git 自带的…
阅读更多...
2/29作业

2/29作业

typedef int datatype; typedef struct link_list { union { int len; datatype data; }; struct link_list *next; }link_list,*link_p; #include "link_list.h" int main(int argc,const char *argv[]) { //创建链表并填入数据 …
阅读更多...
阿里云服务器大降价20%，简单拥有五年三台2h4gECS，组建公网集群

阿里云服务器大降价20%，简单拥有五年三台2h4gECS，组建公网集群

要在阿里云ECS上组建集群&#xff0c;您可以按照以下步骤进行操作&#xff1a; 创建ECS实例&#xff1a;登录阿里云控制台&#xff0c;选择ECS实例&#xff0c;点击“创建实例”按钮。根据实际需求选择实例的配置参数&#xff0c;例如实例规格、操作系统、网络等。根据需要选择…
阅读更多...
Spring Boot Profiles简单介绍

Spring Boot Profiles简单介绍

Spring Boot application.properties和application.yml文件的配置 阅读本文之前&#xff0c;请先阅读上面的配置文件介绍。 Spring Boot Profiles是一个用于区分不同环境下配置的强大功能。以下是如何在Spring Boot应用程序中使用Profiles的详细步骤和代码示例。 1. 创…
阅读更多...
buuctf_web_loveSQL

buuctf_web_loveSQL

题目&#xff1a; 上面有行小红字&#xff0c;“用 sqlmap 是没有灵魂的”,呵呵。。嗯&#xff0c;确实 啥也憋说&#xff0c;先上万能钥匙&#xff1a; a or 11 # a’ or 11 # a" or 11 # 尝试后的结果&#xff0c;可以发现该SQL验证是单引号&#xff0c;a or 11 #注入过…
阅读更多...
预训练大模型LLM的PEFT之—— Prefix Tuning

预训练大模型LLM的PEFT之—— Prefix Tuning

简介 Prefix Tuning是2021.01提出来的&#xff0c;在它之前&#xff0c;我们使用prompt主要是人工设计模板或者自动化搜索模板&#xff0c;也就是prompt范式的第一阶段&#xff0c;就是在输入上加上prompt文本&#xff0c;再对输出进行映射。这种离散模板对模型的鲁棒性很差。…
阅读更多...
【YOLO v5 v7 v8 小目标改进】RFB：组合不同大小的卷积核和扩张卷积来模拟人类视觉感受野的多尺度特性

【YOLO v5 v7 v8 小目标改进】RFB：组合不同大小的卷积核和扩张卷积来模拟人类视觉感受野的多尺度特性

RFB&#xff1a;组合不同大小的卷积核和扩张卷积来模拟人类视觉感受野的多尺度特性 提出背景RFB 原理空间感受野结构RFB-Net 小目标涨点YOLO v5 魔改YOLO v7 魔改YOLO v8 魔改 提出背景 当前表现最好的目标检测器依赖于深层CNN骨干网络&#xff0c;如ResNet-101和Inception&am…
阅读更多...
qt5与qt6的cmake区别

qt5与qt6的cmake区别

文章目录 使用cmake构建qt项目&#xff0c;坑很多。一是本身就麻烦&#xff0c;二是&#xff0c;确实坑&#xff0c;因为不同的qtcreator版本&#xff0c;选了不同的kits&#xff08;套件&#xff09; 生成的CMakeList.txt文件也不一样。 如果可以的话都选择Qt6的相关选项&…
阅读更多...
【C++】认识类和对象

【C++】认识类和对象

&#x1f525;博客主页&#xff1a; 小羊失眠啦. &#x1f3a5;系列专栏&#xff1a;《C语言》 《数据结构》 《C》 《Linux》 《Cpolar》 ❤️感谢大家点赞&#x1f44d;收藏⭐评论✍️ 文章目录 一、什么是面向对象&#xff1f;二、类的引入三、类的定义四、类的访问限定符与…
阅读更多...
一文速览深度伪造检测（Detection of Deepfakes）：未来技术的守门人

一文速览深度伪造检测（Detection of Deepfakes）：未来技术的守门人

一文速览深度伪造检测&#xff08;Detection of Deepfakes&#xff09;&#xff1a;未来技术的守门人 前言一、Deepfakes技术原理卷积神经网络&#xff08;CNN&#xff09;&#xff1a;细致的艺术学徒生成对抗网络&#xff08;GAN&#xff09;&#xff1a;画家与评审的双重角色…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023