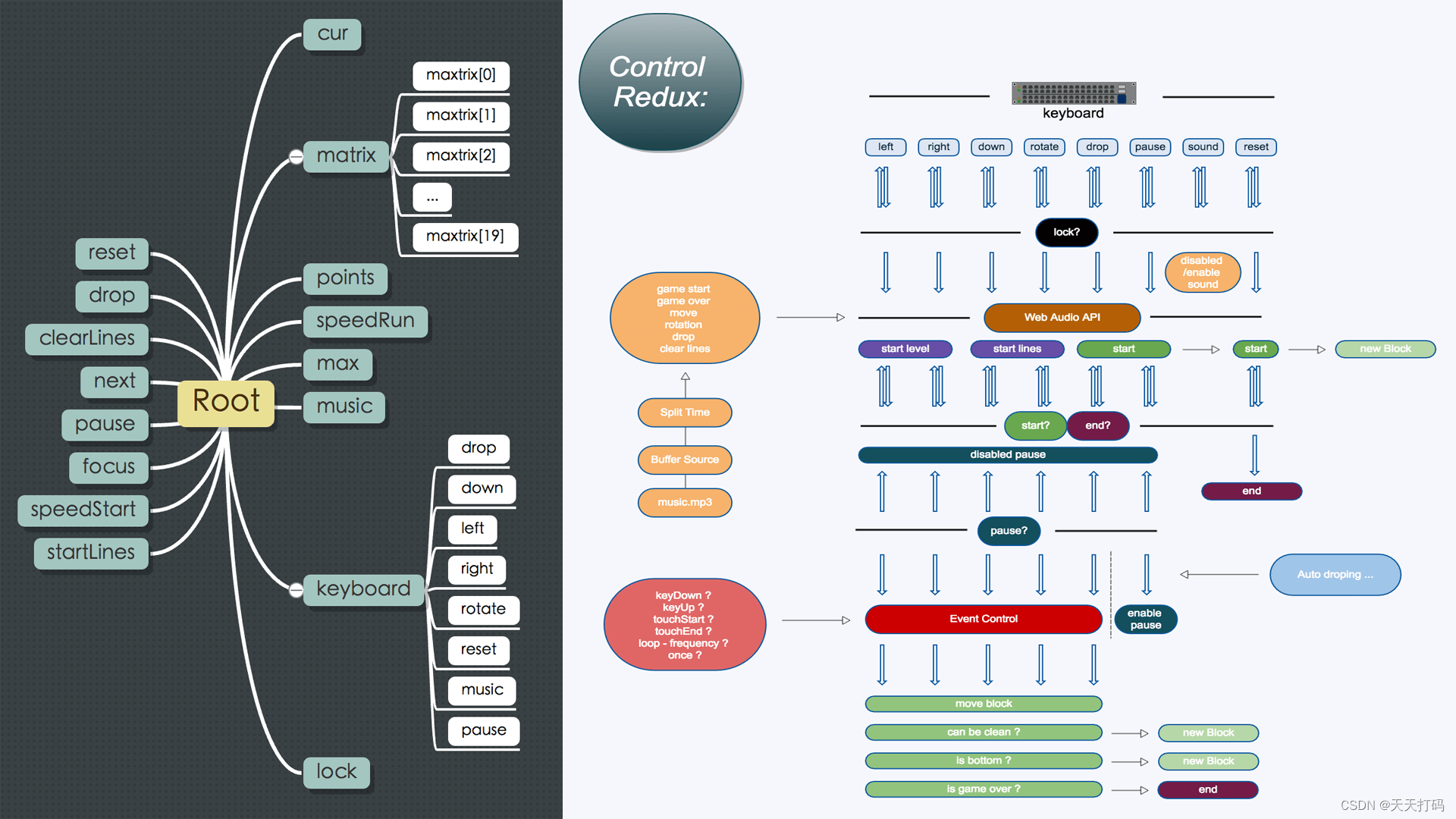
定义

路径长度：从根结点到该结点所经过的边数。
叶子结点的带权路径长度：叶子结点的权值*路径长度
树的带权路径长度：所有叶子结点的带权路径长度之和

哈夫曼树：带权路径长度最小的树，也称最优二叉树。

构造

反复选择两个最小的元素合并，直至只剩下一个元素。
因此可以选择用优先队列（小根堆结构）实现，由顶部弹出两个最小的，相加结果压入，直至合并只剩下一个数，此时累加和即是最小带权路径长度。
因此，哈夫曼树没有度为1的结点，且权值越大的结点离根结点越近

应用

#include <iostream>
#include <queue>
using namespace std;
//定义一个long long型的小根堆
priority_queue<long long,vector<long long>,greater<long long>> q;
int main(){
    int num;
    long long value,sum=0,x=0,y=0;
    cin>>num;
    for(int i=0;i<num;i++){
        cin>>value;
        q.push(value);//自动由小到大排序
    }
    while(q.size()>1){
        x=q.top();
        q.pop();
        y=q.top();
        q.pop();
        sum+=x+y;//最小带权路径长度
        q.push(x+y);
    }
    cout<<sum<<endl;
    return 0;
}

2.哈夫曼编码
求给定字符串长度最短且唯一的编码。得到的哈夫曼树，为其左子树编号为0，右子树编号为1，所组成的序列即是。