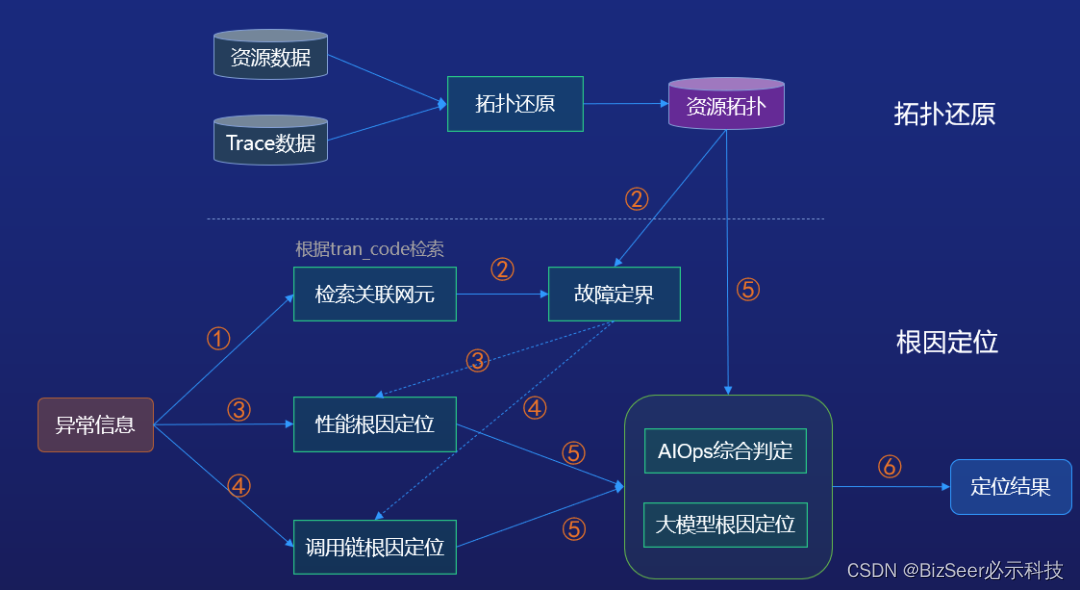
Word2vec算法优化

J(θ): 损失函数
问题:进行每个梯度更新时,都必须遍历整个语料库,需要等待很长的时间,优化将非常缓慢。
解决:不用梯度下降法,用随机梯度下降法 (SGD)。
减少噪音,做得更好,也可以更快的计算。
词向量的随机梯度
我们只更新实际出现的向量(当前中心词和上下文)
Word2vec算法:更多细节
为什么需要两个向量表示一个词:
- 更容易优化,最后取平均最终表示词
- 可以只用一个向量,不过做微分复杂很多
Word2vec算法实际是一个算法家族
- Skip-grams (SG) (更常用,合理自然)
- Continuous Bag of Words (CBOW)
目前介绍的都是简单的 softmax等式来训练

更有效的训练方法:负采样(SGNS)
Skip-grams负采样

目标函数

我们希望中心词和真实上下文词的向量点积最大,中心词和随机词的向量点积最小。
k是我们负采样的样本数目(随机采样的数量)

unigram分布是 单词在语料库中实际出现的频率。
(10000个词出现50次 => 50/10000)
Why not capture co-occurrence counts directly?
共现矩阵,将单词表示为共现向量(单词之间共同出现的次数)
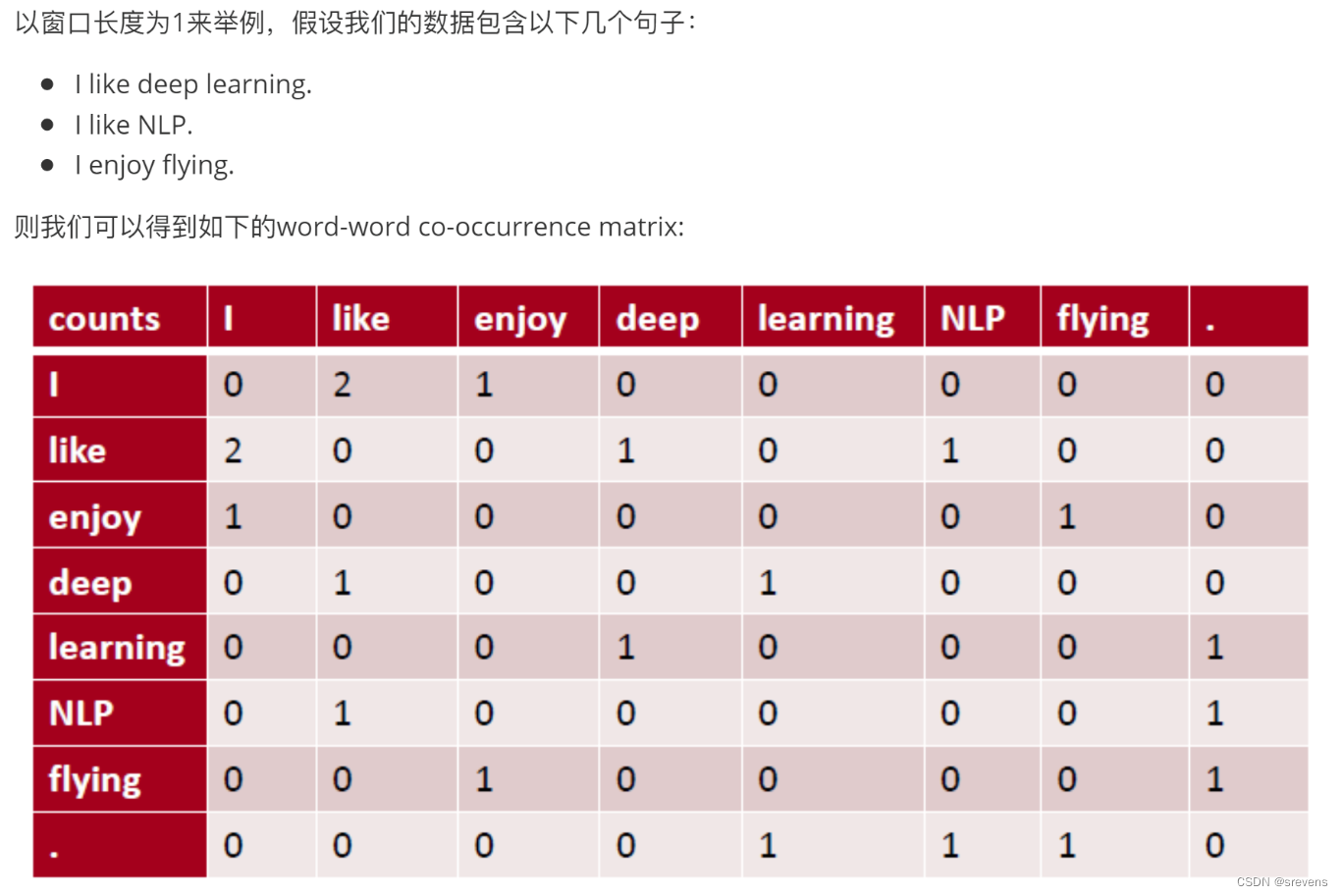
两种方式实现共现矩阵:
- windows:与Word2vec类似,在每个单词周围都使用window。捕获了位置和一些更细微的句法和近似语义。
- full document:将窗口大小设置为段落大小或整个网页,并计算其中的共现。经常用于信息检索(潜在的语义分析)

第一种方法:Dimensionality Reduction on X (SVD)
为了得到低维度的词表示。
它能够在给定的维度内,尽可能的恢复到原始的共现矩阵。


问题:
最终得到的单词计数不是正态分布的。因为有大量的常用词和稀有词。
第二种方法:Hacks to X
按比例调整计数,处理词频较高的问题。
对原始计数取log/限制最大计数/扔掉虚数
接下来运行SVD来获得更有用有效的词向量。
总结
两种词向量表示方法:
- 共现矩阵,然后使用线性代数方法(SVD)
(问题:词之间没有意思层面的联系,只是相似性;过分重视大计数) - 随机初始,然后使用迭代神经网络更新算法(梯度下降法 负采样)
(问题:语料库很大,分母太难计算;没有有效利用数据)

Glove:将两种表示方法结合起来 => 在神经网络中使用计数矩阵
|||
V
向量差异的编码意义
关键思想:共现概率的比值可以对meaning component进行编码
重要的不是单一的概率大小,而是他们的比值,蕴含着meaning component。
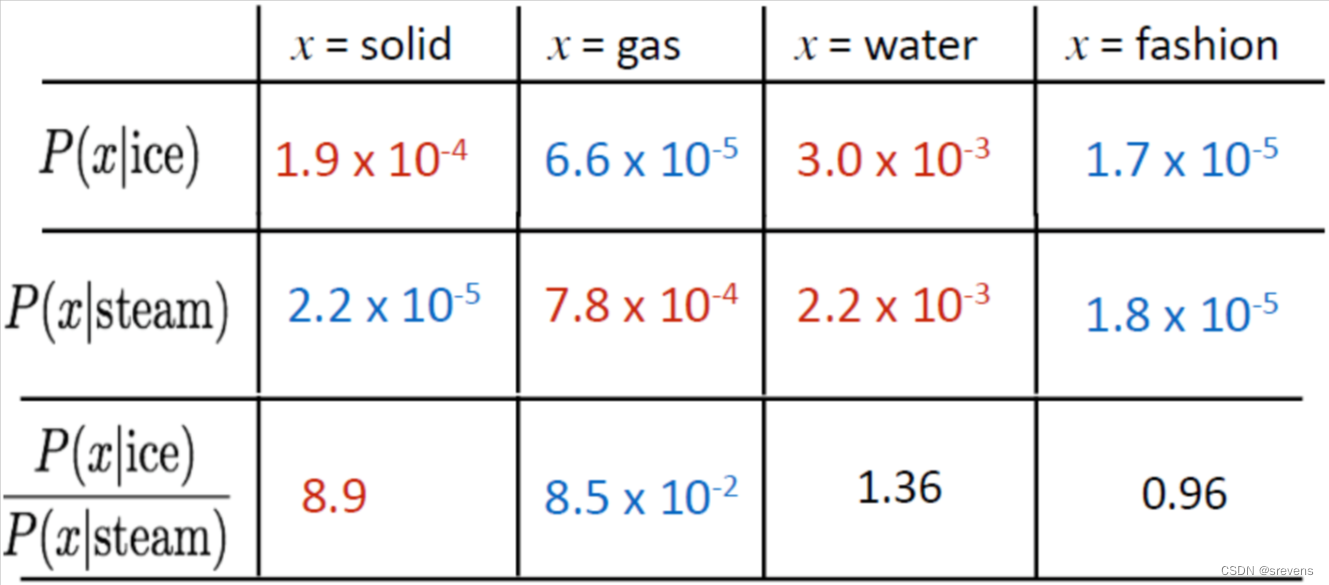
ice 和 solid 共现的概率是 P 1 = 1.9 × 1 0 − 4 P1 = 1.9 \times 10 ^ {-4} P1=1.9×10−4
steam 和 solid 共现的概率是 P 2 = 2.2 × 1 0 − 5 P2 = 2.2 \times 10 ^ {-5} P2=2.2×10−5
ice和solid共现概率 和 steam和solid共现概率 的比值是 P 1 P 2 \frac{P1}{P2} P2P1
我们如何将这些共现概率的比率 作为线性的meaning components来捕获?因此,在我们的词向量空间中,我们可以加上和减去线性的meaning components。(能够得到 king-man = queen-woman)
方法:构建一个log-bilinear模型
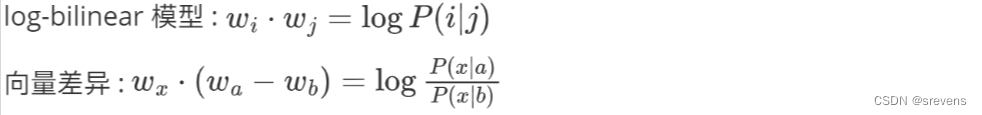
我们希望 两个词向量之间的点积 试图逼近 共现概率的对数
这样就可以获得特性:两个向量之间的差异 等于 共现概率比的对数
我们希望这些东西是相等的!所以我们希望最小化它们的差异。

Glove:在共现矩阵上使用神经网络模型的方法 尝试统一共现矩阵模型和神经网络模型之间的思想。
- 共现计数矩阵模型直接使用共现计数矩阵来表示词语之间的关系(共现计数矩阵固定已知)
- 而神经网络模型则使用神经网络结构来建模。
损失函数 J 将它们统一了起来。它结合了神经网络模型中的词向量表示
w
i
w_i
wi 和
w
~
j
\tilde{w}_j
w~j ,以及共现计数矩阵模型中的共现计数矩阵
X
i
j
X_{ij}
Xij,并且通过优化这个损失函数来学习词向量。
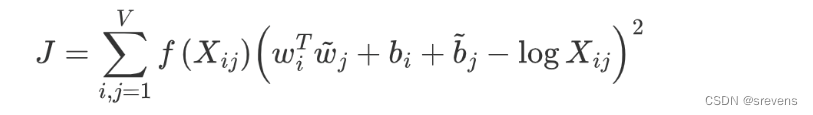
· J J J 是衡量词向量表示质量的损失函数,是我们希望最小化的目标。
· ∑ i , j = 1 V \sum_{i,j=1}^V ∑i,j=1V表示对所有词对的共现情况进行求和, V V V 是词汇表的大小。
· f ( X i j ) f(X_{ij}) f(Xij) 是一个函数,会根据一个词的频率来缩放它,它用来对常见词进行限制。
X表示共现矩阵, X i j X_{ij} Xij 表示词 i i i 和词 j j j 的共现计数。
· w i w_i wi 和 w ~ j \tilde{w}_j w~j 是词 i i i 和词 j j j 的词向量。
· b i b_i bi 和 b ~ j \tilde{b}_j b~j 是词 i i i 和词 j j j 的偏置项。用于修正(如果某个单词的概率很高),使得模型能够更灵活地拟合数据。
· log X i j \log X_{ij} logXij 是共现计数的对数。
使用平方,使得结果总是正的,我们希望最小化J。
可以直接在共现计数矩阵上优化损失函数J(共现计数矩阵固定已知),怎么优化?
- 初始化参数:随机初始化词向量矩阵 W W W和 W ~ \tilde{W} W~,以及偏置项 b b b和 b ~ \tilde{b} b~。
- 计算损失函数的梯度:计算损失函数 J J J 关于参数的梯度,包括词向量 W W W 和 W ~ \tilde{W} W~, 以及偏置项 b b b 和 b ~ \tilde{b} b~ 的梯度。
- 更新参数:使用梯度下降法 根据计算出的梯度来更新参数。更新的公式通常为:
θ t + 1 = θ t − α ∇ J ( θ t ) \theta_{t+1}=\theta_t-\alpha\nabla J(\theta_t) θt+1=θt−α∇J(θt)
其中, θ \theta θ表示参数(词向量矩阵和偏置项), α \alpha α表示学习率, ∇ J ( θ ) \nabla J(\theta) ∇J(θ)表示损失函数 J J J 关于参数 θ \theta θ的梯度。 - 重复步骤2和3:重复计算梯度并更新参数,直到达到停止条件 (例如达到最大迭代次数、损失函数收敛等)。
将共现计数矩阵模型和神经网络模型的思想结合在一起,形成了损失函数 J,带来了以下好处:
- 训练快速:它直接基于共现计数进行优化(共现计数矩阵固定已知),不需要像之前的神经网络模型那样每次迭代计算都超级复杂。
- 可扩展性:共现计数矩阵的存储和处理相对简单,具有很好的可扩展性,能够轻松地应用于大型语料库。而且训练过程中不需要太复杂的计算或大量的参数,使得它能够有效地处理大规模的数据。
- 适用于小型数据集和低维向量:它结合了共现计数矩阵模型和神经网络模型的优点,既可以捕捉词汇之间的共现信息,又可以通过神经网络模型来学习词向量之间的复杂关系,从而能够在各种规模的数据集和向量空间中表现良好。
- 总结: 共现计数矩阵模型在处理大规模语料库时具有高效性和简单性,而神经网络模型则可以更好地捕捉词向量之间的复杂关系。结合了两者的思想,可以兼顾模型的高效简单性和表达能力。
我们如何才能真正评估词向量?
- 内在评估:内在评估是通过词向量自身的性质和特征来评估其质量,而不依赖于具体的应用场景。
- 例如词类比任务:如使用"king - man + woman"来验证是否得到"queen"。如果词向量的性质良好,那么通过向量空间中的数学运算可以得到类似的类比关系。最后计算出正确次数的准确性得分。
- 外在评估:通过将词向量应用于具体的自然语言处理任务来评估其性能(网络搜索、机器翻译…)
- 例如命名实体识别任务:使用词向量作为特征输入到命名实体识别模型中,如CRF、RNN、LSTM等,并根据模型在测试数据集上的准确率、召回率、F1分数等性能指标来评估词向量的效果。

内在评估:词类比任务
通过向量空间中的加法和余弦相似度来寻找与给定类比关系最相似的词向量。
!可能得到的d就是原来的c,所以最后的结果不考虑三个输入词中的任意一个。

Glove可视化
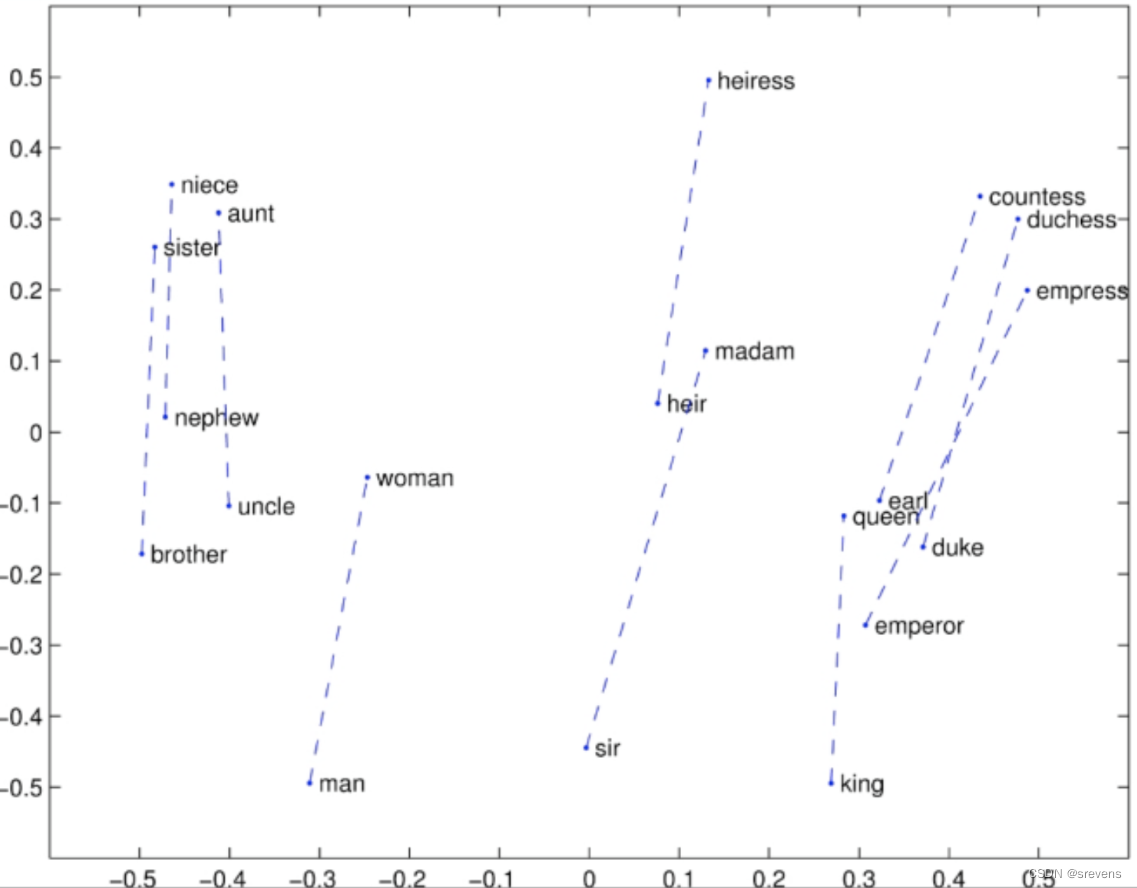
Glove可视化:Company - CEO
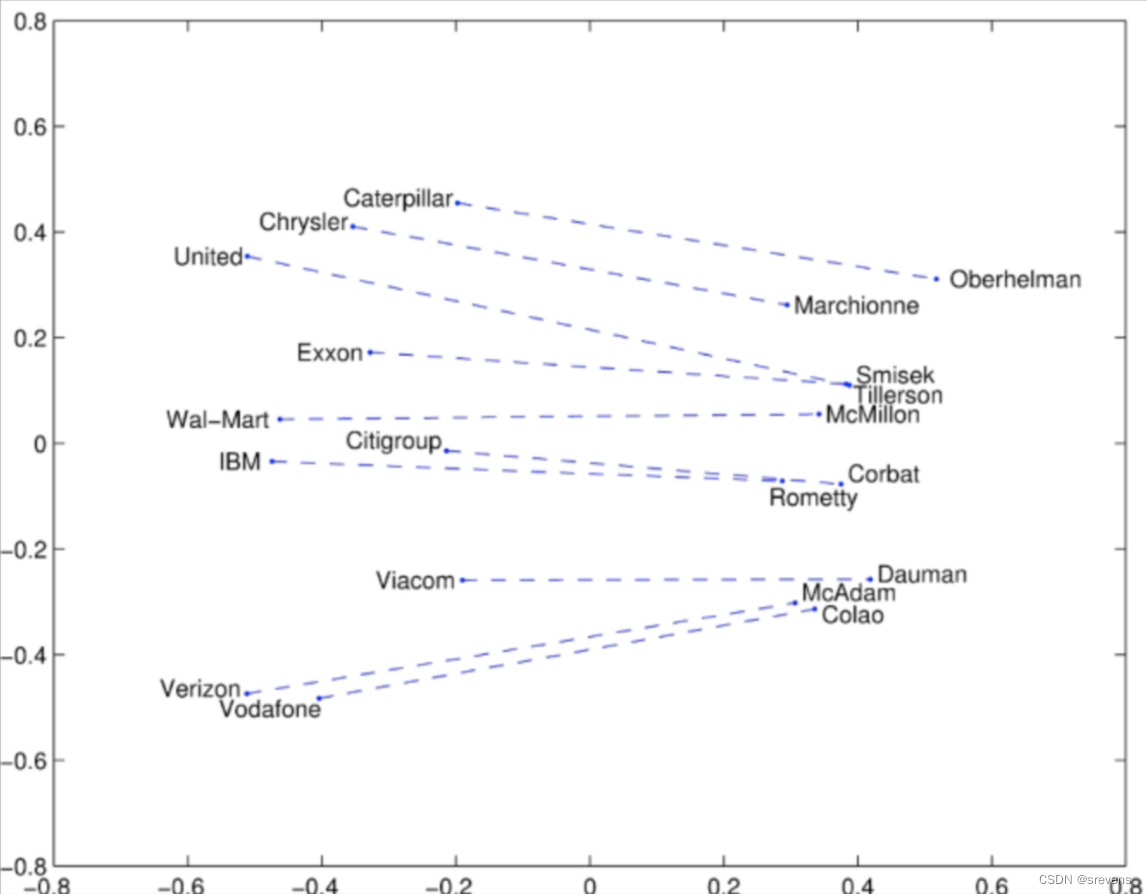
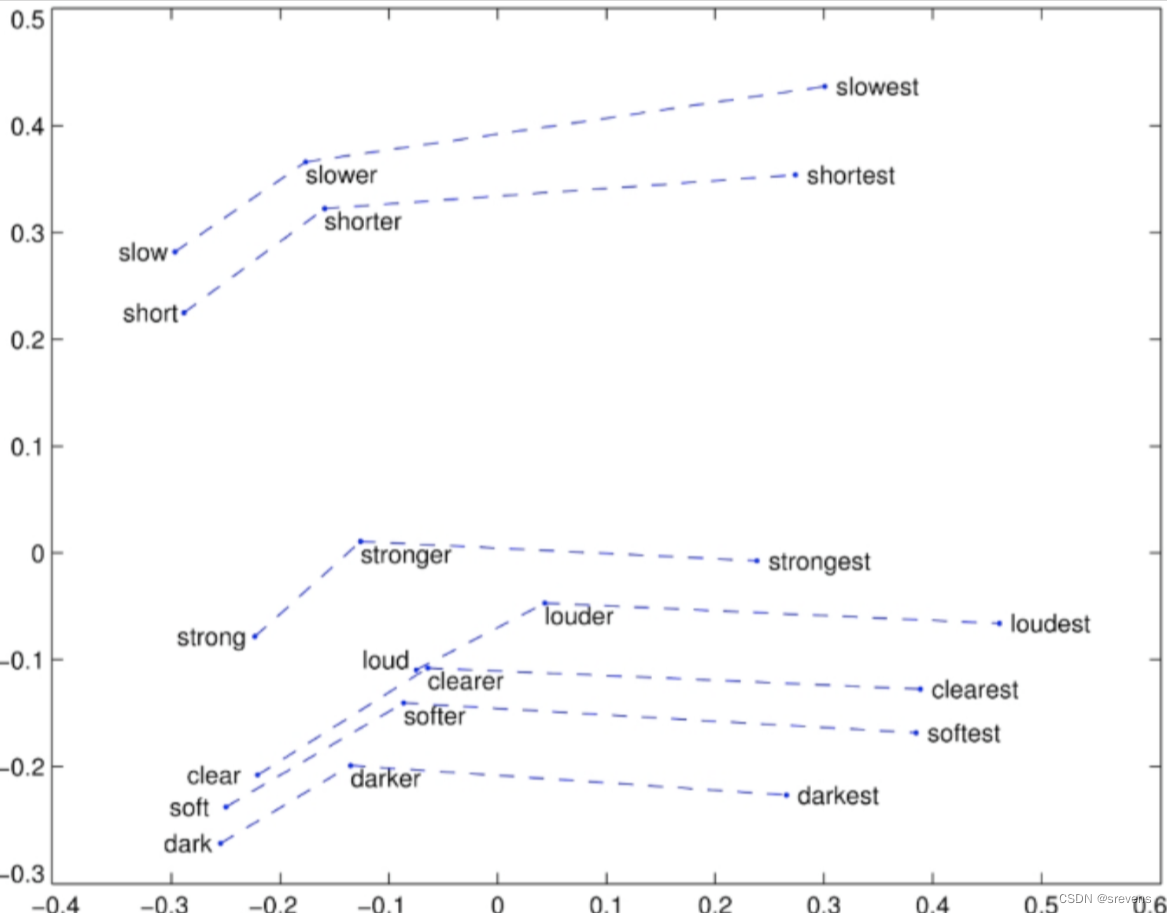
Glove可视化:比较级和最高级
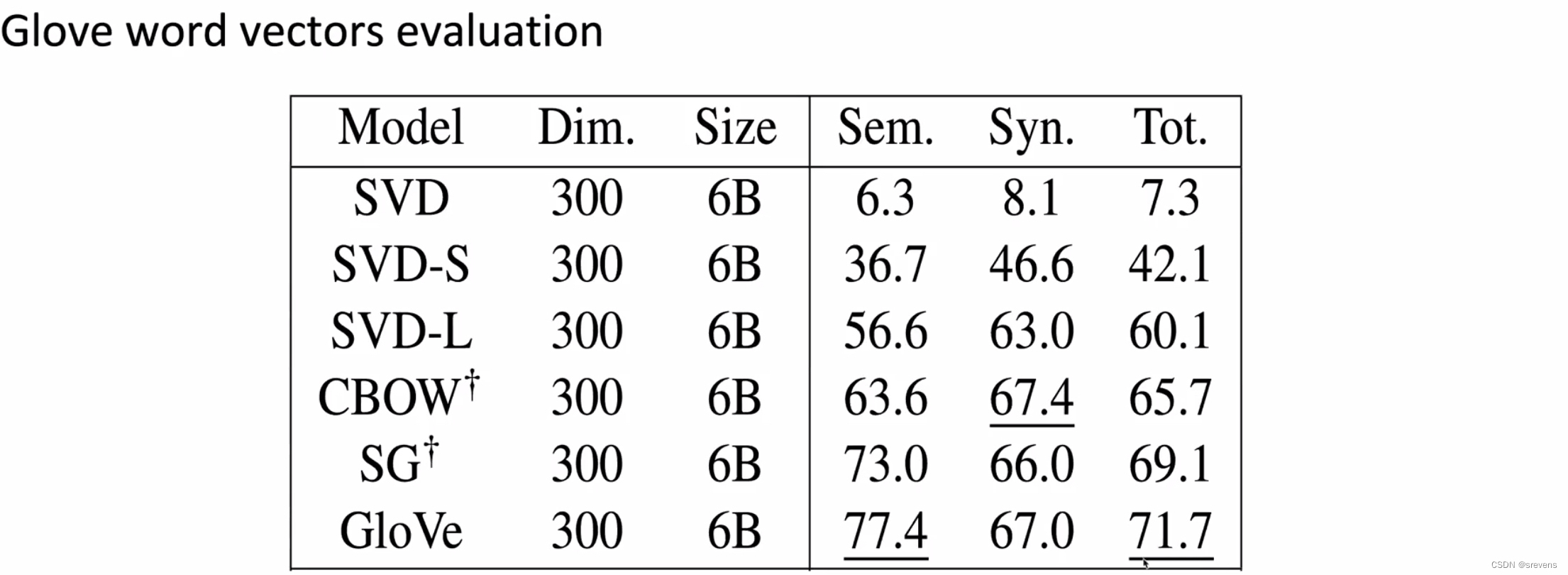
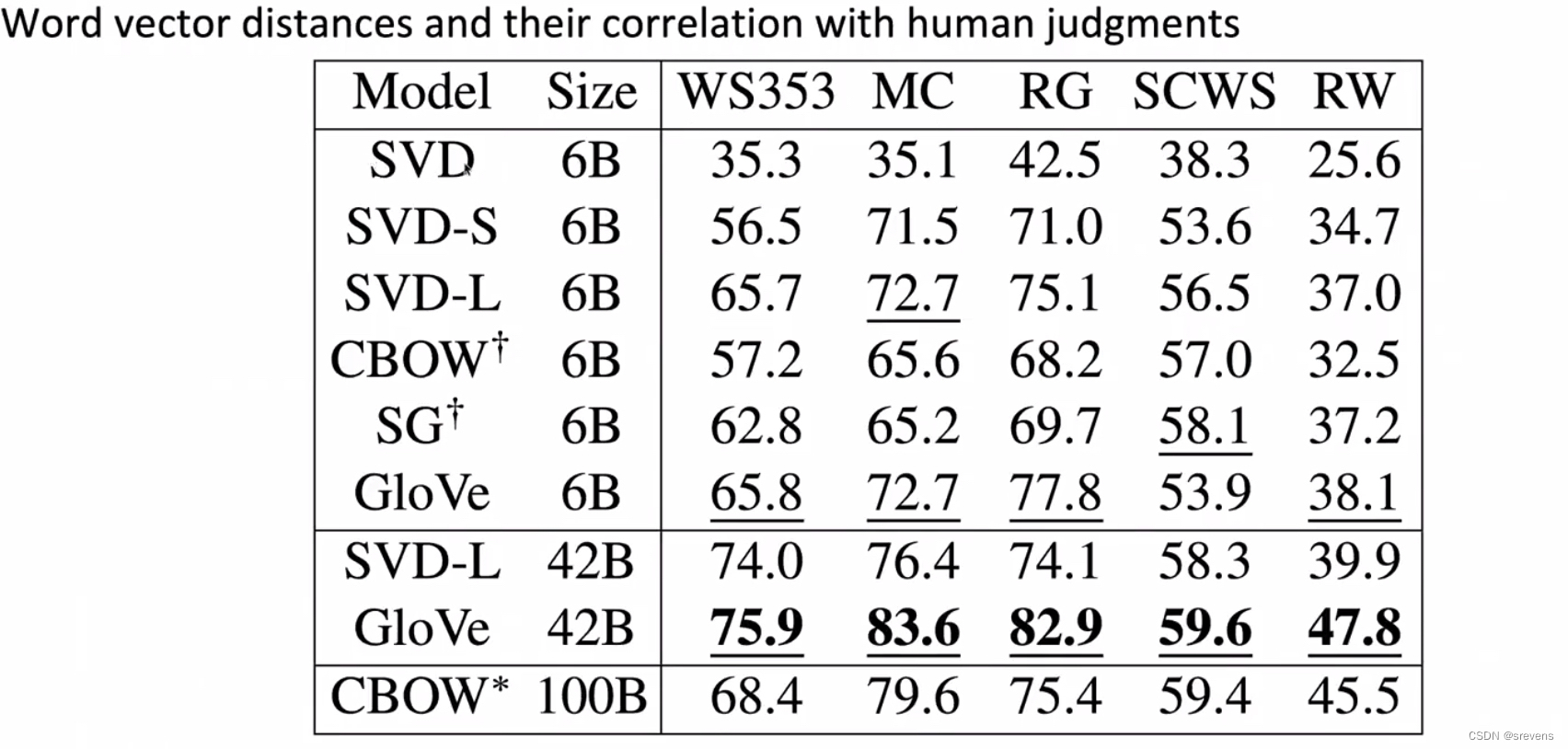
SVD:通过不缩放的共现矩阵模型
SVD-S, SVD-L:通过缩放的共现矩阵模型
CBOW, Skip-grams:通过Word2vec算法,神经网络模型
Glove:结合共现矩阵模型和神经网络模型之间的思想
但是事实证明上面的表中的数据有错误。Glove模型表现好的主要原因是训练的数据集更好:
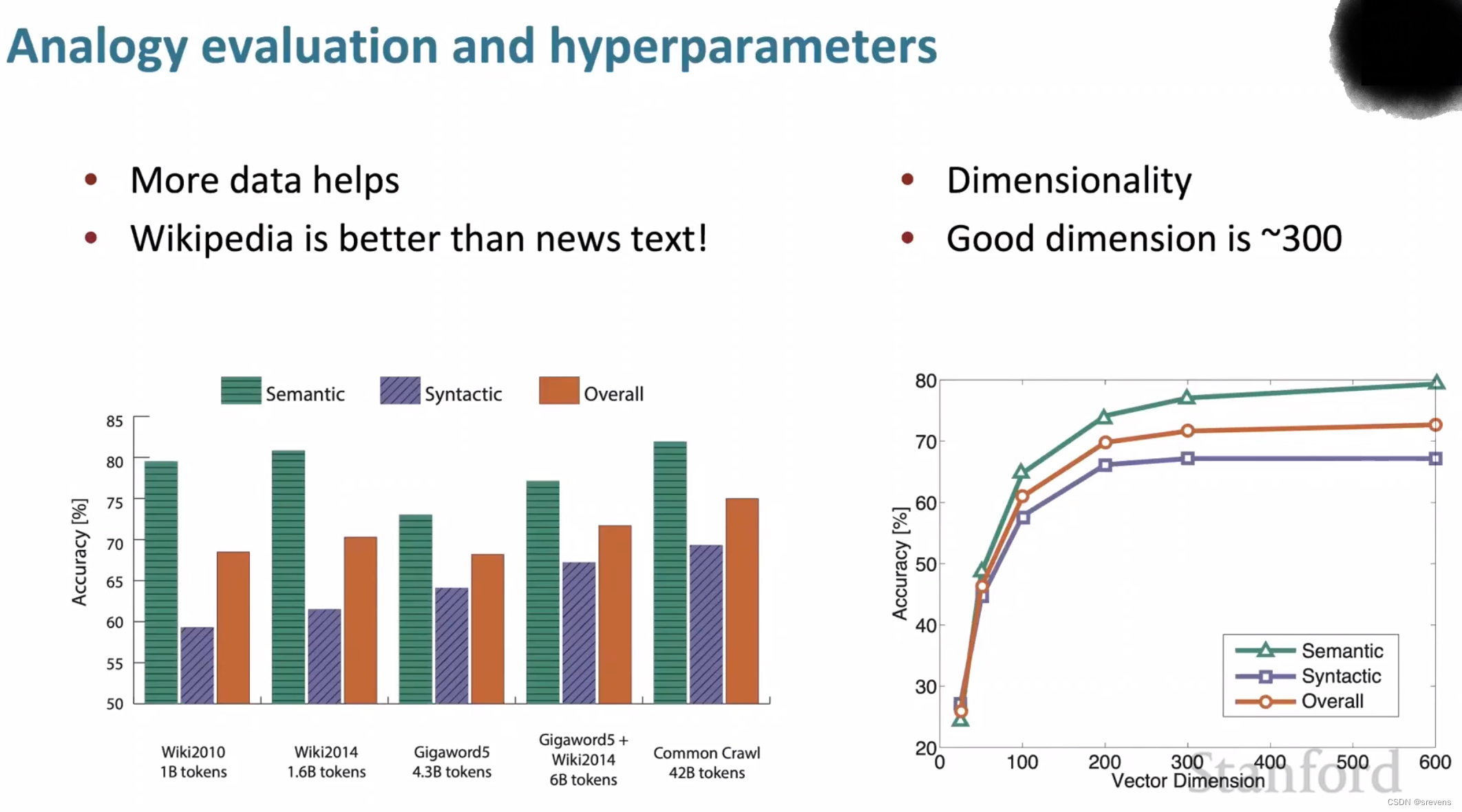
- 数据集越大越好,并且维基百科数据集比新闻文本数据集要好,因为:
- 维基百科就是在解释概念以及他们之间的相互关联,更多的说明性文本显示了事物之间的所有联系。
- 而新闻并不去解释,而只是去阐述一些事件。
- 300是一个很好的词向量维度
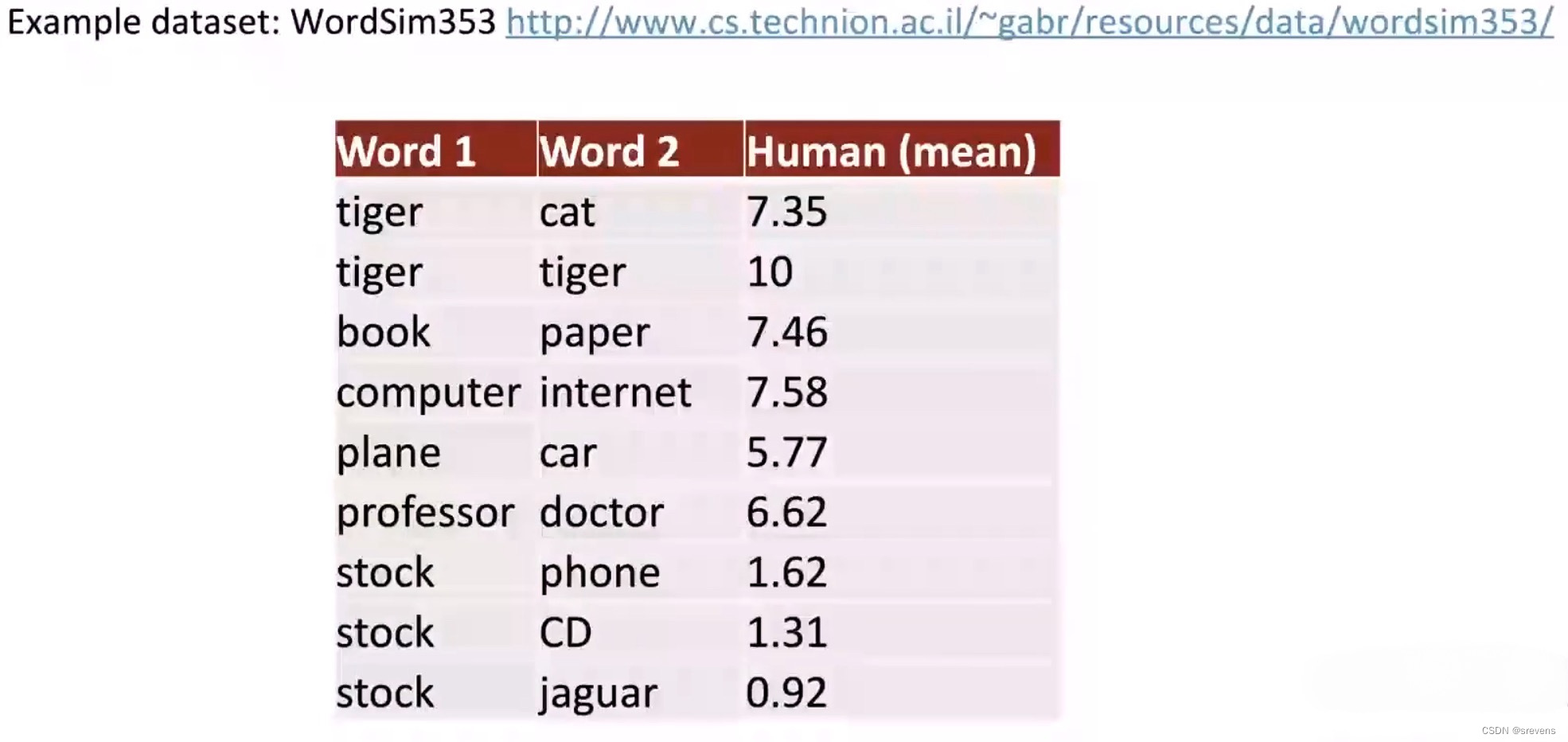
内在评估:相似性评估
人类给一对单词一个相似度分数(0~10),然后根据多个人类的判断进行平均。
外在评估:命名实体识别
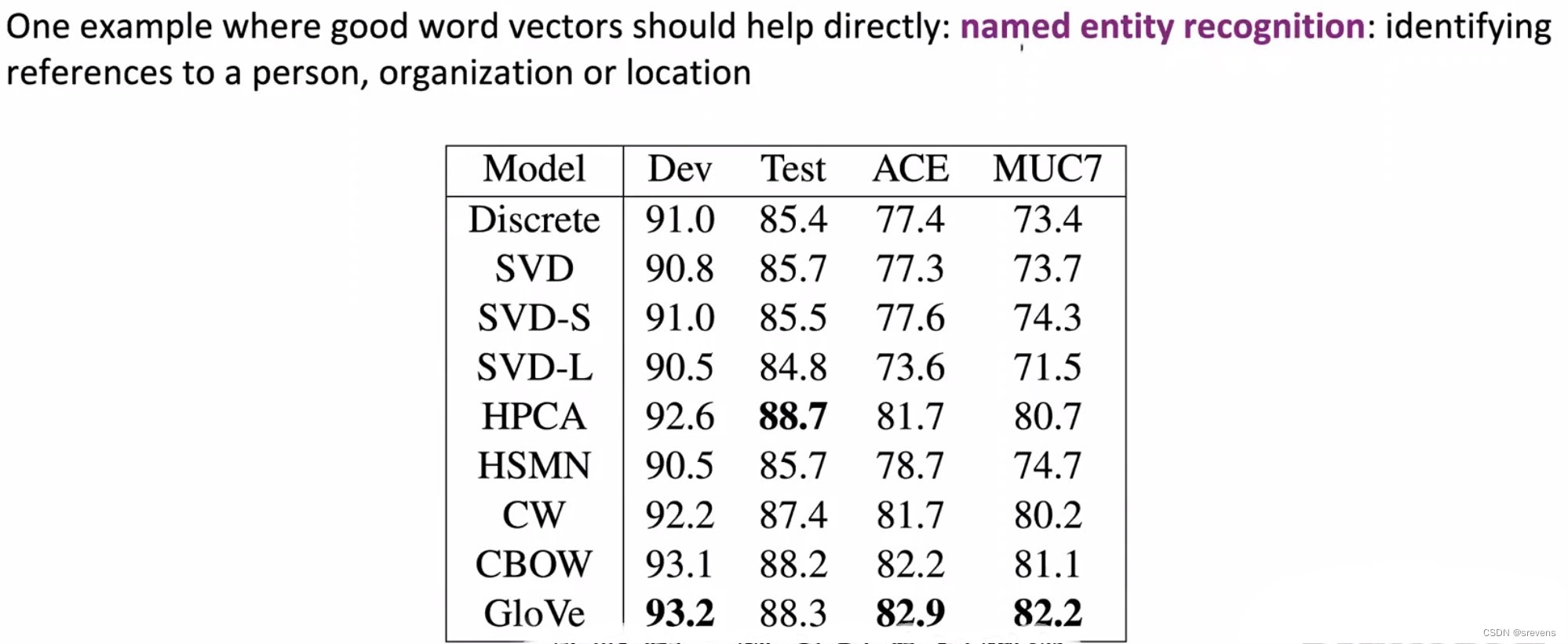
Discrete:仅有离散特征的模型
词义
大多数多次都是多义的
- 特别是常见的单词
- 特别是存在已久的单词
例子:pike

解决方法:一个词多个词向量
Improving Word Representations Via Global Context And Multiple Word Prototypes (Huang et all 2012)
思想:

将常用词的所有上下文进行聚类,通过该词得到一些清晰的簇,从而将这个常用词分解为多个单词,例如
b
a
n
k
1
:银行
bank_1:银行
bank1:银行,
b
a
n
k
2
:界限
bank_2:界限
bank2:界限。
- 这样做有点复杂:首先必须学习语义,然后根据语义开始学习词向量。
- 一个词的不同意思不是很好分类,可能重叠。如何将词义切割成不同的含义总是有点不清楚。
解决方法:不同含义的加权和得到一个词向量
单词在标准单词嵌入(如word2vec)中的不同含义以线性叠加(加权和)的形式存在
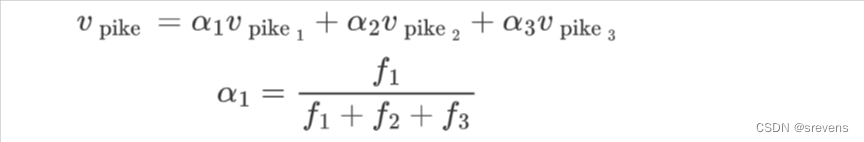
只是加权平均值就已经可以获得很好的效果,自我消除歧义,可以说相似的词向量已经包含在内(作为加数)
我们普遍觉得将不同意思的向量加起来,就很难区别它们。
- 就像如果 1 + 2 + 3 + 4 => 10,
- 那么10是不可以往回的:10 =X> 1 + 2 + 3 + 4
但是在高维向量空间中的单词非常稀疏。我们可以使用自稀疏编码的思想来分离出不同的意思。
- 前提是它们相对比较常见
所以可以 "pike"向量 开始,实际分离出对应于 "pike"这个词 的不同含义的向量的成分。
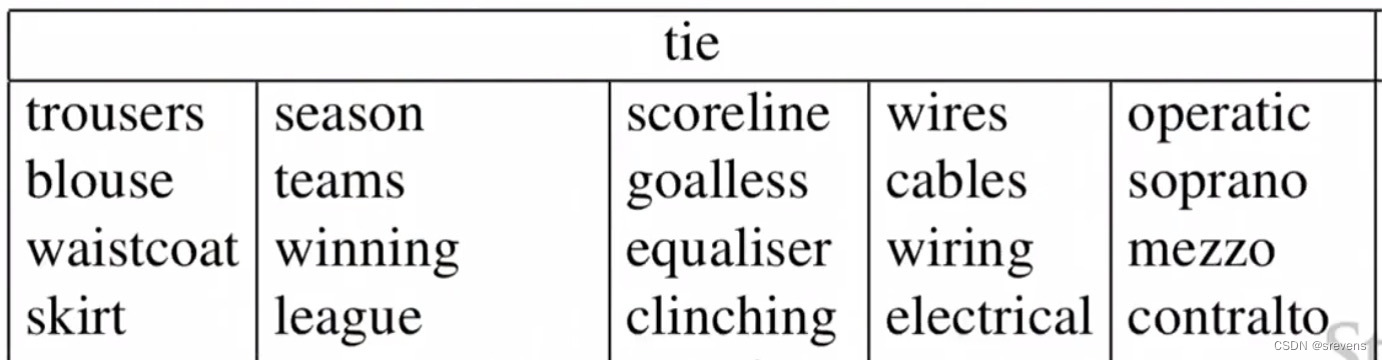
比如:对于 "tie"词向量,可以分离成五种意思: