459. 重复的子字符串

题目描述

给定一个非空的字符串 s ，检查是否可以通过由它的一个子串重复多次构成。

示例 1:

输入: s = “abab”
输出: true
解释: 可由子串 “ab” 重复两次构成。

示例 2:

输入: s = “aba”
输出: false

示例 3:

输入: s = “abcabcabcabc”
输出: true
解释: 可由子串 “abc” 重复四次构成。 (或子串 “abcabc” 重复两次构成。)

提示：

• 1 <= s.length <= 10⁴
• s 由小写英文字母组成

暴力

这段代码的工作原理如下：

1. 外层循环每次将字符串s的下一个字符加入到子串a中，这个子串可能是重复的单元。
2. 内层循环尝试用子串a去匹配整个字符串s。
3. 如果在某次内层循环中，a成功地匹配了整个s（其中count用于跟踪a在s中重复的次数），那么函数返回true。
4. 如果a在任何点上失败（字符不匹配），内层循环将会中断，并且外层循环继续尝试下一个可能的子串。

该算法是一个基本的解法，对于每个可能的子串进行尝试，时间复杂度为O(n^2)，其中n是字符串s的长度。在最坏的情况下，例如当字符串为全部由相同字符组成时，这个解法可能会比较慢。更高效的算法可能会使用KMP算法或字符串哈希来降低复杂度。

// 定义解决方案类
class Solution {
public:
    // repeatedSubstringPattern成员函数，接受一个字符串s
    bool repeatedSubstringPattern(string s) {
        // a用于存储当前正在检查的子串
        string a="";

        // 循环遍历字符串的前半部分
        // 如果s能由子串重复构成，那么子串的长度不会超过s长度的一半
        for(int i=0; i < s.size() / 2; i++) {
            // 将当前字符添加到子串a中
            a += s[i];

            // count用于记录当前已匹配的字符数
            int count = 0;
            // k用于在子串a中的比较位置
            int k = 0;
            
            // 遍历整个字符串s
            for(int j = 0; j < s.size(); j++) {
                // 如果字符匹配，增加已匹配的字符数，移动k到下一个位置
                if(s[j] == a[k]) {
                    count++;
                    k++;
                    // 如果已匹配字符数等于子串a的长度
                    if(count == a.size()) {
                        // 如果此时已经到达s的末尾，则返回true
                        if(j == s.size() - 1)
                            return true;
                        // 重置已匹配字符数和子串a的比较位置
                        count = 0;
                        k = 0;
                    }
                } else {
                    // 一旦遇到不匹配的情况，立即跳出内层循环
                    break;
                }
            }
        }
        // 如果循环结束都没有找到符合条件的子串，返回false
        return false;
    }
};

移动匹配

当一个字符串s：abcabc，内部由重复的子串组成，那么这个字符串的结构一定是这样的：

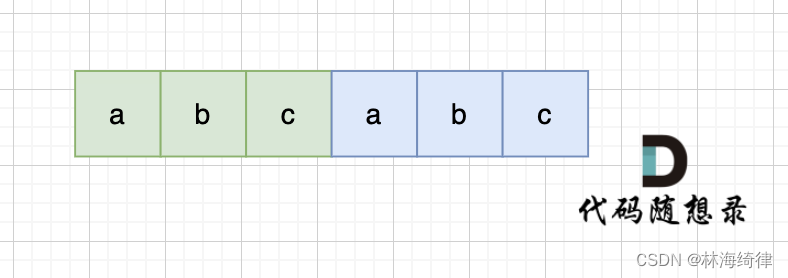
也就是由前后相同的子串组成。

那么既然前面有相同的子串，后面有相同的子串，用 s + s，这样组成的字符串中，后面的子串做前串，前面的子串做后串，就一定还能组成一个s，如图：

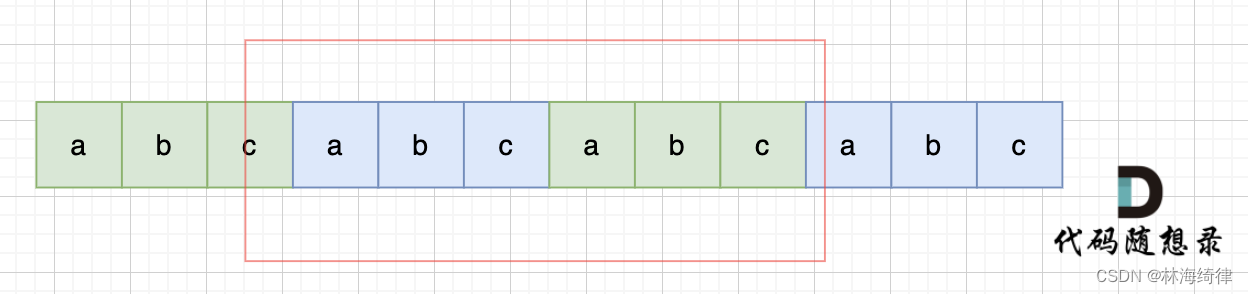
所以判断字符串s是否由重复子串组成，只要两个s拼接在一起，里面还出现一个s的话，就说明是由重复子串组成。

当然，我们在判断 s + s 拼接的字符串里是否出现一个s的的时候，要刨除 s + s 的首字符和尾字符，这样避免在s+s中搜索出原来的s，我们要搜索的是中间拼接出来的s。

代码如下：

// 定义解决方案类
class Solution {
public:
    // 定义成员函数repeatedSubstringPattern，它接受一个字符串s
    bool repeatedSubstringPattern(string s) {
        // 创建一个新字符串t，由字符串s重复拼接一次得来，这样任何s的重复子串模式都会在新字符串t中出现两次
        string t = s + s;

        // 从t的开头删除一个字符，这是为了除去原始字符串的单独完整出现
        t.erase(t.begin());
        // 从t的尾部删除一个字符，同样是为了确保消除原始字符串的单独完整出现
        t.erase(t.end() - 1);

        // 在新字符串t中寻找原始字符串s
        // 如果发现s存在于t中（并且不是在开头或者结尾，因为那些位置已经被删除了）
        // 那么说明s可以由它的一个子串通过重复多次构成
        if (t.find(s) != -1) return true;

        // 如果在t中找不到s作为子串，说明s不能由它的子串通过重复构成，返回false
        return false;
    }
};

• 时间复杂度: O(n)
• 空间复杂度: O(1)
• 不过这种解法还有一个问题，就是 我们最终还是要判断 一个字符串（s + s）是否出现过 s 的过程，大家可能直接用contains，find 之类的库函数。 却忽略了实现这些函数的时间复杂度（暴力解法是m * n，一般库函数实现为 O(m + n)）。

如果我们做过 28. 找出字符串中第一个匹配项的下标 题目的话，其实就知道，实现一个 高效的算法来判断 一个字符串中是否出现另一个字符串是很复杂的，这里就涉及到了KMP算法。