tip

数组下标从0开始还是从1开始

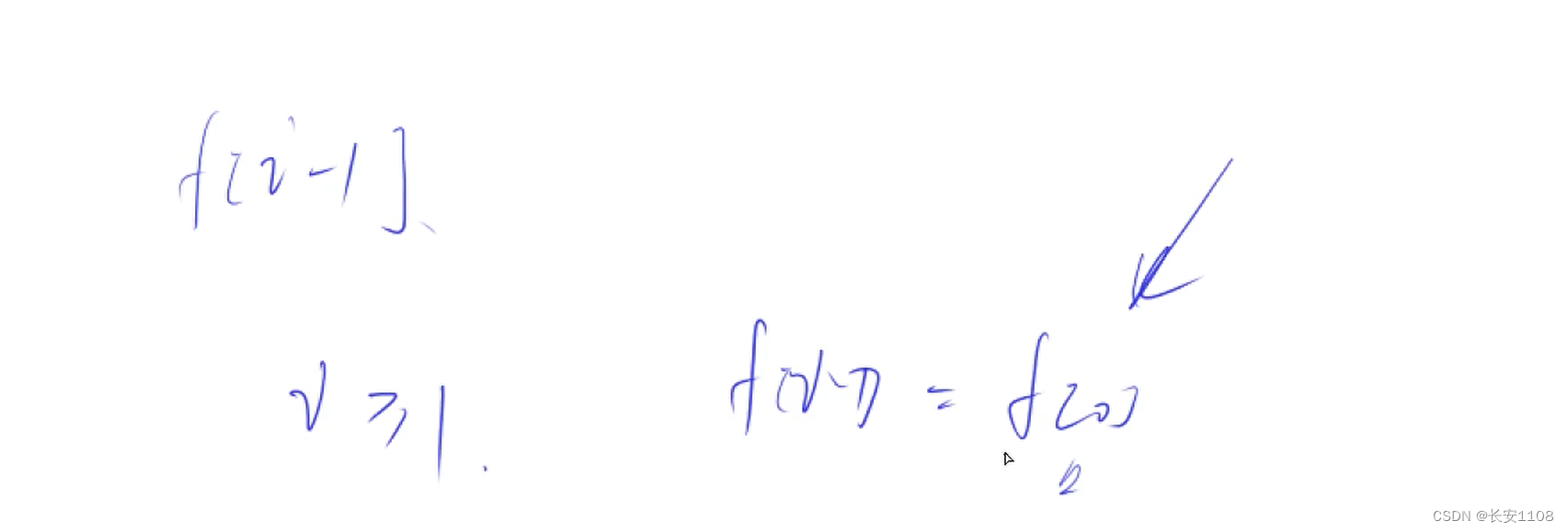
如果代码中涉及到数组下标为i-1（有时候哪怕不是同一个数组也符合情况，因为是针对同一组数据进行的多个数组设置），那么我们可以使 i 从 1开始，这样，当 i = 1 时，就取到了[0]，如果这个位置有特殊情况，那么这样一来我们也不必使用 if ，直接对 f [0]设置一个特殊值即可

注意，“输入”与“使用”是统一的，即如果输入数组时决定了使用 i 从 1 开始，那么到时候使用或者取元素时，一定要记得是从 1 开始，
如果输入决定了是从0开始，那么到时候取元素的时候，记得从0开始

数学三角形

介绍

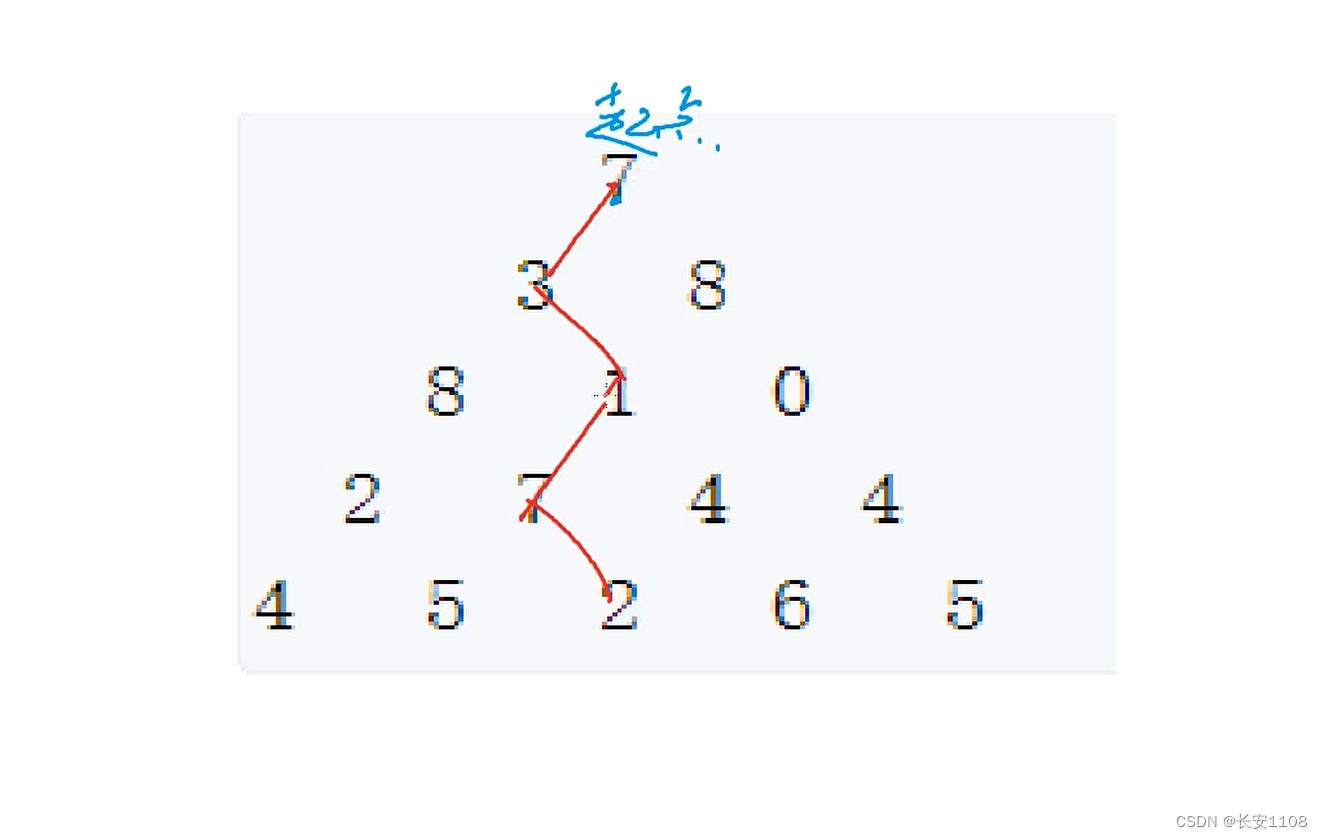
从顶部出发，可以向左下或者右下移动，最后形成一条路径，找到一条路径使得路径上的数字之和最大

算法思想

首先我们对三角形的各个数进行编码，从上到下每行从1开始表上行号，之后，东北方向偏45度进行列号的编排，最左边是1列，之后往右依次是2，3，…，这样一来，我们就可以标定某个元素的位置，这也符合三角形位置的数据在数组内存储时的位置

对于动态规划，仍然是状态表示和状态计算，
状态表示：因为每个元素由一个二维数对进行位置表示，所以，状态表示仍然是一个二维的，如上图所示，属性是max
状态计算：由前面的经验可以总结出：状态计算是一个情况的划分，划分的是上一层的情况，即仅研究上一层即可，之后递推原理会帮助代码完成
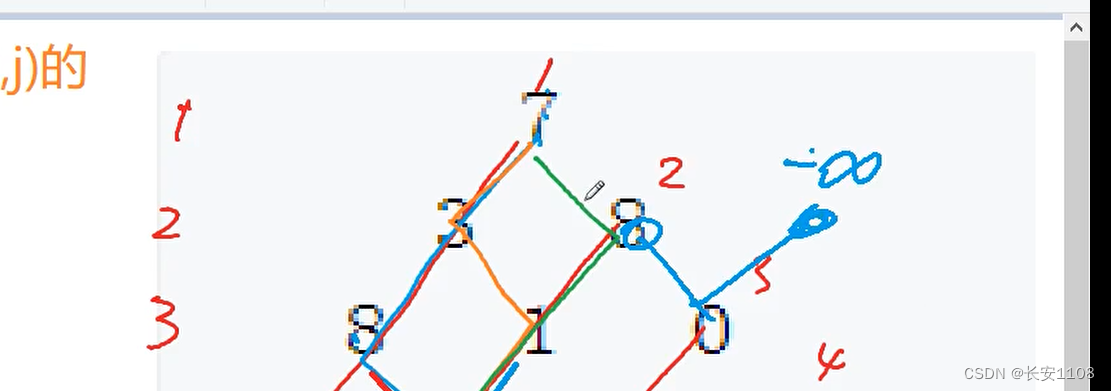
上一层的状态有两个，一个来自左上，一个来自右上。
两种划分都是曲线救国的思路，即 f [ i - 1 , j - 1 ] + a[ i , j ]，另一个是 f [ i - 1 , j ] + a[ i , j ]
其中 a数组存储了所有的数据，a [ i , j ]就是表示[ i , j ]位置的值

例题+代码

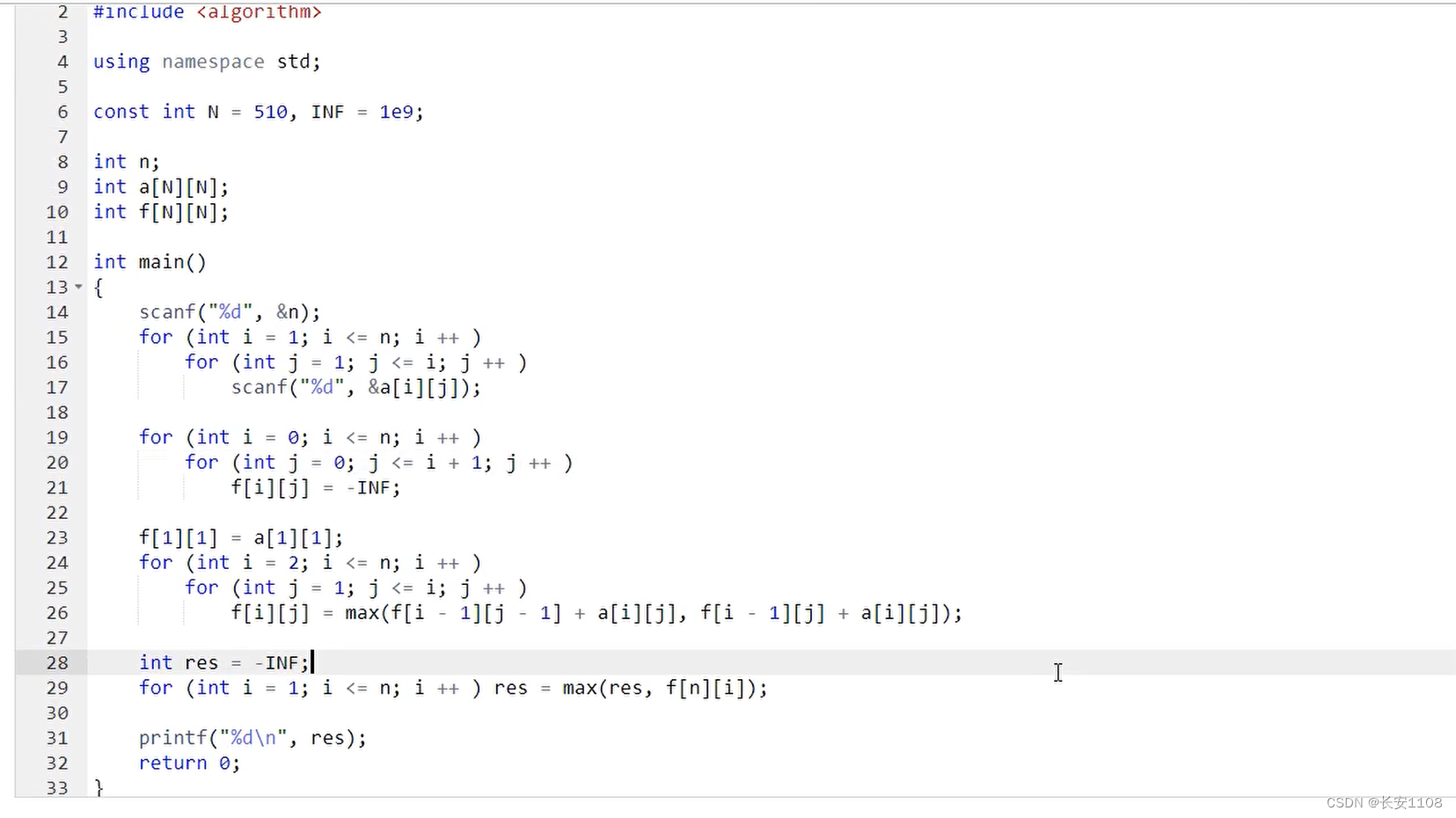
首先，a[N][N]数组是用来存储所有的数据的
f[N][N]是状态表示

之后，main函数里
首先读入n
之后由于这组数据会涉及到 i-1 ，所以使用数组存数据时，i从1开始到小于等于n，j从1开始到小于等于 i （因为是三角形），读入到a[][]数组中，给[0][x] [x][0]这些位置空出来，方便一些特殊情况时拿来使用（包括a数组自己使用或者其他数组使用，总之这个位置要留出来）
之后初始化状态表示，因为状态表示数组涉及到某一点的上边两个角，所以，要处理好边界问题，我们的 i 从 0开始到等于n，j 从 0开始到等于 i + 1 （这样做可以在原来的数据基础上，多加一个0行和0列被初始化，这样的话，当我们遇到如下图所示情况时，就不会出错了），且f[i][j] = - INF，将所有的位置初始化为负无穷，这样的话，最终原数据的外面的位置下标，f[][]的值是负无穷，这样做是为了当我们有路径来到了原数据的外面，那最后的值一定是负无穷，这样我们就可以筛选出来哪些路径是经过了原数据的外面的位置得到的，这些数据可以排除
之后初始化f[1][1] = a[1][1]，因为第一个还没有经过任何其他的点，可以初始化为1
之后for循环，i 从 2 开始到等于n（之所以从2开始，是因为1就一个节点，已经被初始化了）
二层循环 ，j 从 1 开始到等于i （仍然是因为输入时是三角形输入）
f[ i ][ j ] = max（f[ i - 1 ][j - 1] + a[ i ][ j ] , f[ i - 1 ][ j ] + a[ i ][ j ]）
到此为止，我们就已经可以拿到所有 i j 点的状态了，我们由于是想求最大路径，所以对叶子结点的状态进行求max即可，这里由于之前所有的f都被初始化为了负无穷，所以这样答案也初始化为负无穷去进行比较，而就算有路径经过了负无穷，那最后的值是-INF+一些正数，肯定比-INF要大一点点，所以，res用-INF存储，最后参与到max中

最长上升子序列

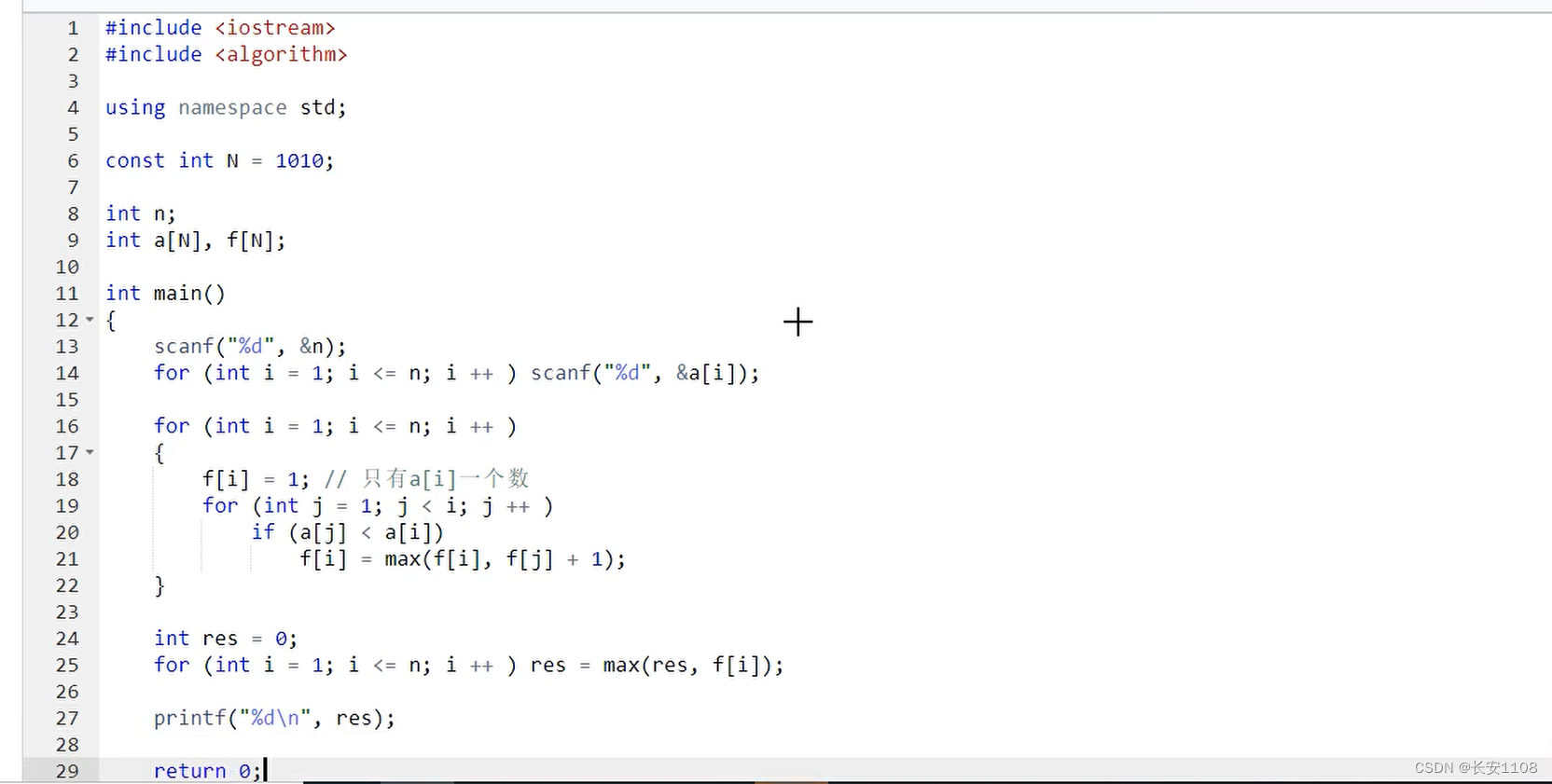
介绍

例如这样一个序列，最长子序列就是 1 2 5 6，长度最长是4

算法思想

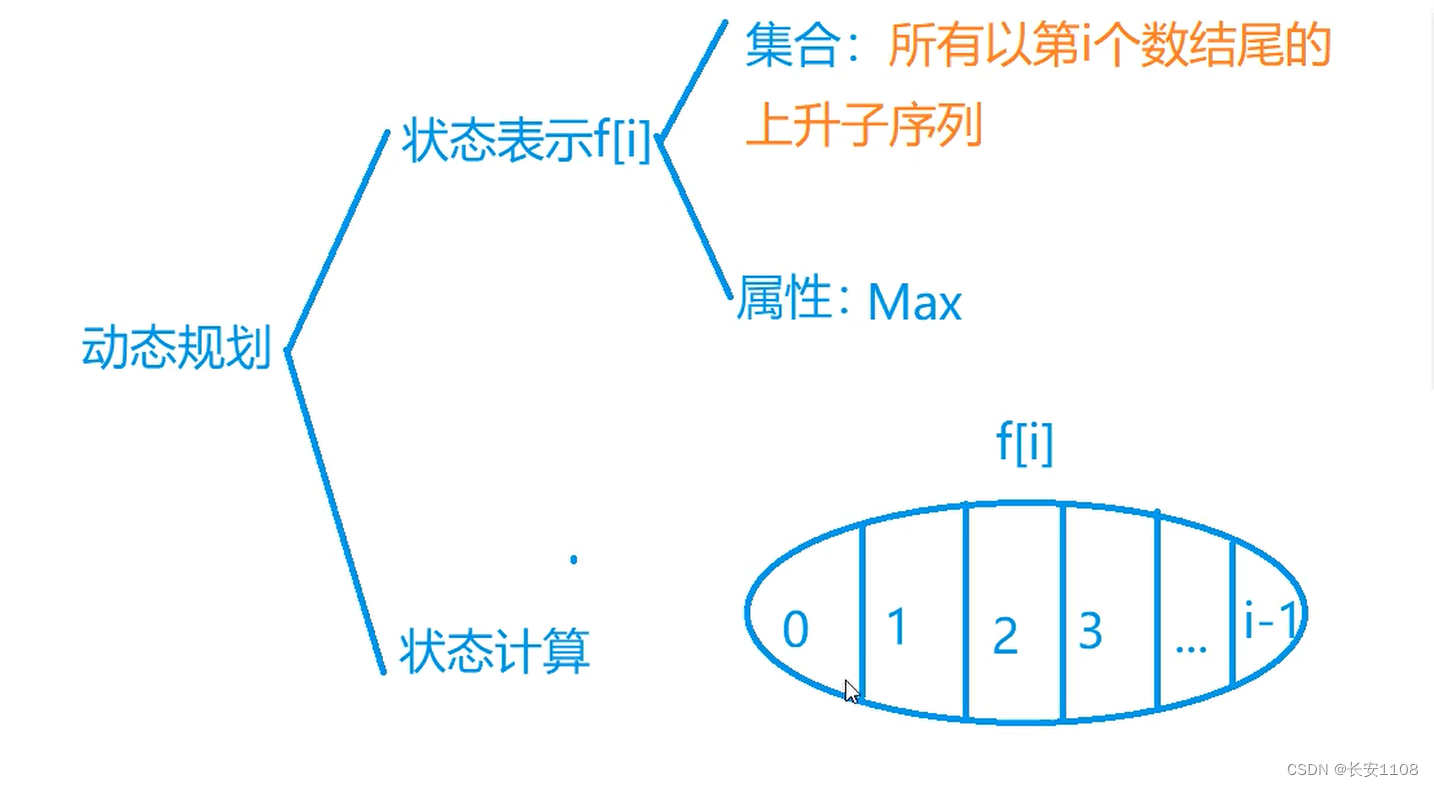
状态表示可以使用一维的，即所有以“第” i 个数结尾的上升子序列，属性是max
状态计算：
划分依据：上一层是第几个数
如果上一层没有数，那么说明只有“第i个数”这一个数
如果上一层的数是第 j 个数，那么可以递推为 f [ j ] + 1（这个j是有条件的，要满足aj < ai）
最后对所有的f[ j ] + 1 （j从0开始到 i - 1）取max就是答案

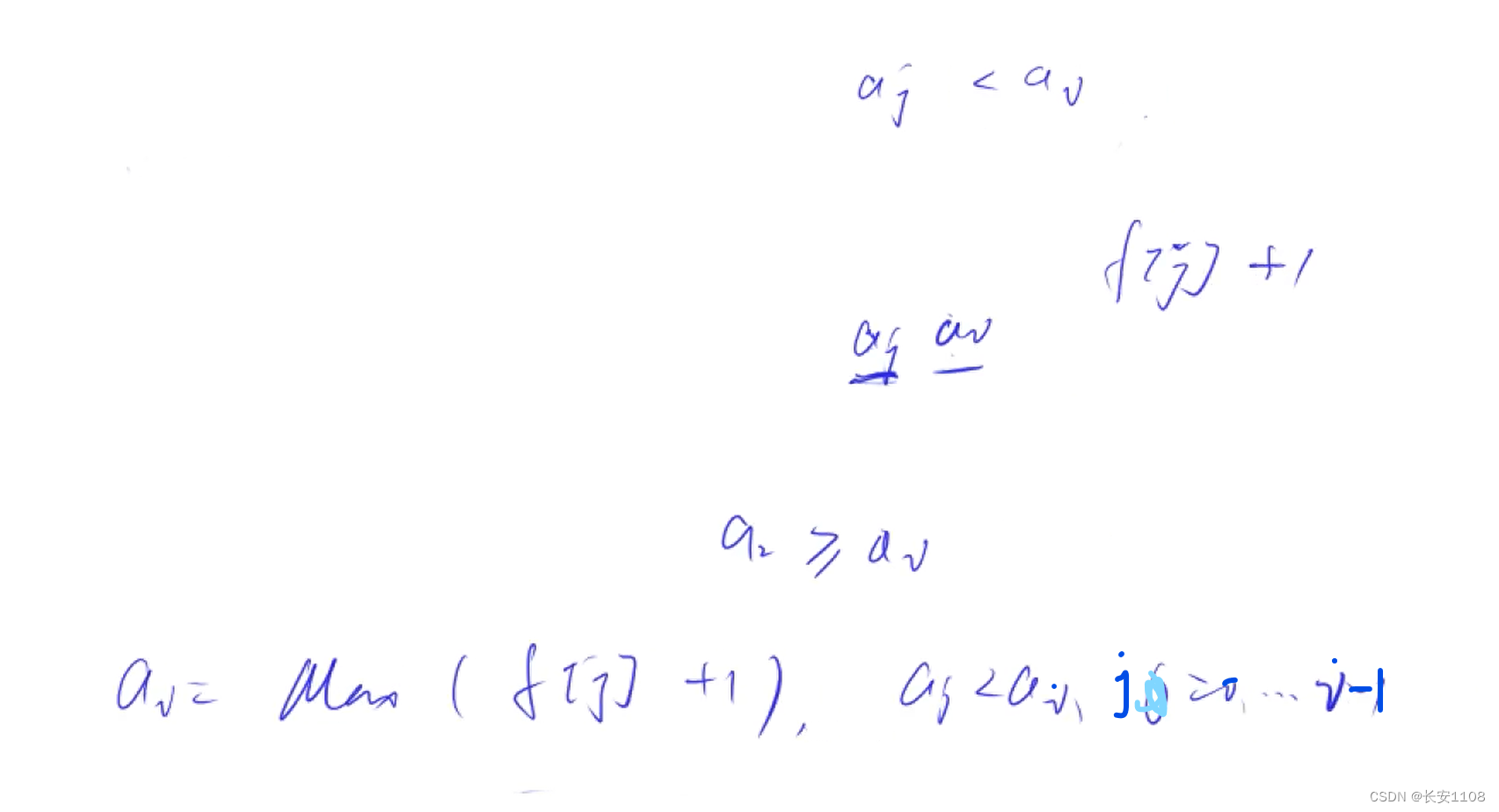
例题+代码

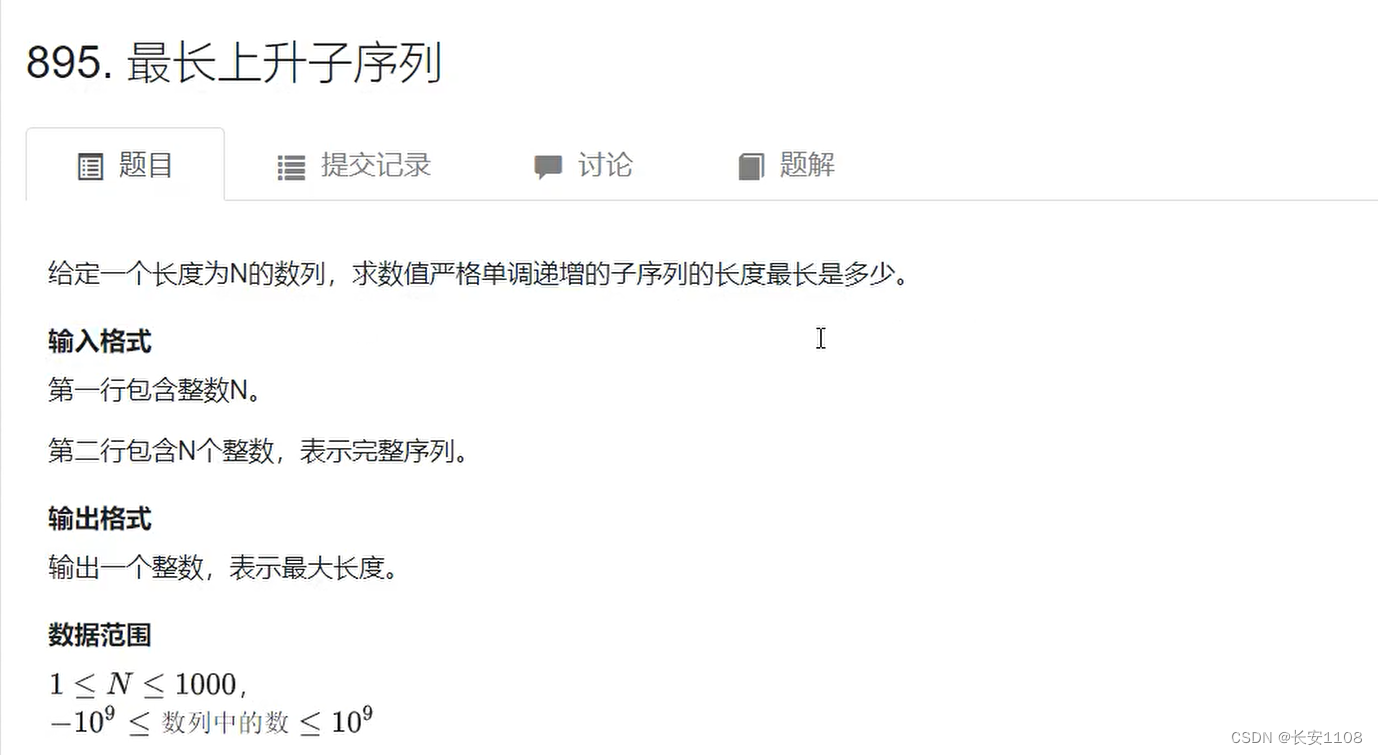
a数组表示将数据进行存储，f数组表示状态表示
在mian函数中
首先输入n
i 从 1 到等于n ，输入a[ i ]
之后对for从1到等于n
f[ i ] = 1 ,（所有的 f 最少是1，所以先初始化为1）
之后，对于for循环，j 从 1 开始到小于 i （因为状态计算时，是以" "前一个数"是第几个数 " 进行划分的，所以j从1到小于i，表示遍历所有划分的情况，为后续取max做准备，这样就可以找到最大的子序列对应的是哪个 j ，因为每个j对应的f[j] 是不同的）
同时判断 if （a[j] < a[i]）才是合法的（因为是上升子序列，要求单调）
之后 f[i] = max(f[i] , f[j]+1)（对所有的划分进行max）

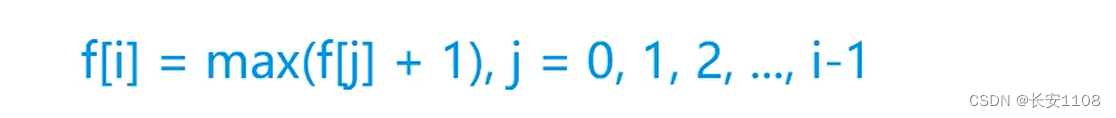
最后，把所有的 f[i] 进行取max，即，将所有的情况取最大值，就是最大子序列

补充：

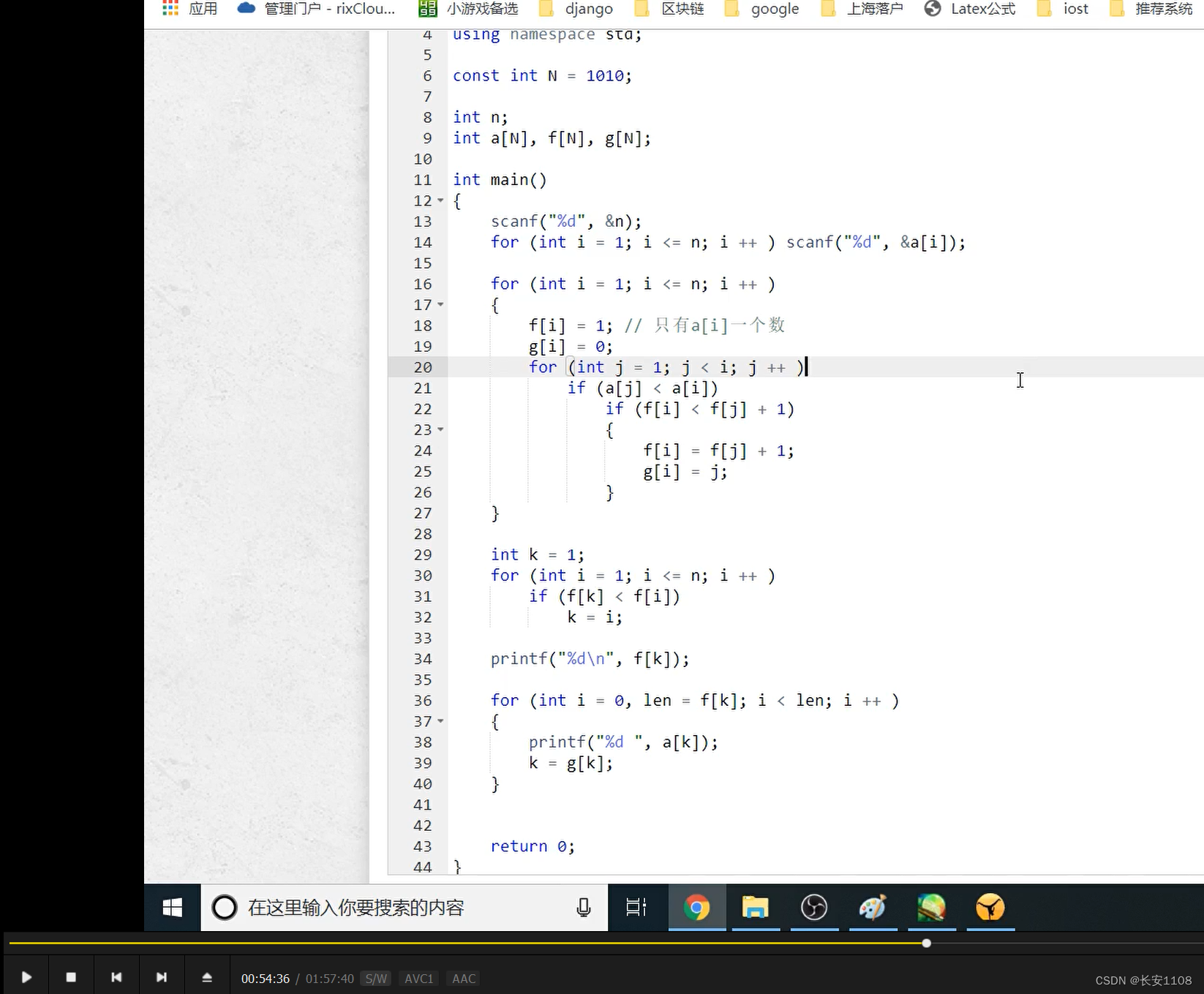
在“动态规划（2）”中00：54时，介绍了如何将最长子序列保存下来

最长公共子序列

介绍

算法思想

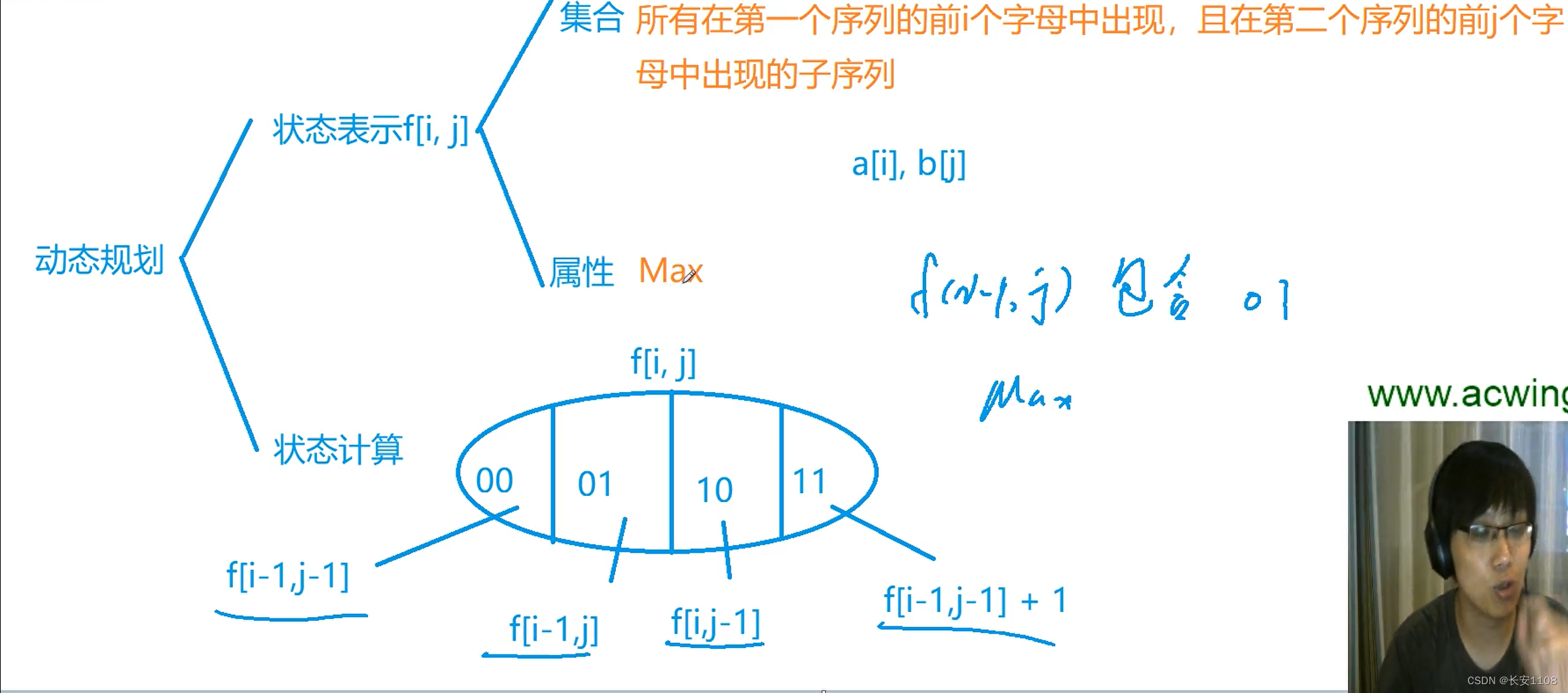
首先，对于状态表示，集合方面，表示所有在第一个序列的前i个字母中出现，且在第二个序列的前 j 个字母中出现的公共子序列，属性是max

之后对于状态计算
可以对公共子序列是否包含a[i] b[j]进行划分，0表示不包含，1表示包含，如上图
之后对于00：
f [ i - 1 , j - 1]
对于11：
f [ i - 1 , j - 1]
对于上面这两个，毫无疑问，确实是这样表示的，
但是对于01和10，我们下面这种表示，是错误的，拿01举例来说，我们想要的是不包含ai但是必须要有bj，而f [i - 1 , j ]表示不包含ai，但是可以有bj也可以没有，所以他是错的，但是f [i - 1 , j ]包含了01这种情况，由于我们是求最大值，而且f的属性也是max，所以，既然f [i - 1 , j ]包含了01的情况，那么就可以拿来进行对比，因为如果对于f [i - 1 , j ]来说，如果01是其所有情况的最大值，那么就符合我们的要求，如果不是，那么我们也没必要再关注01了，而是其他某种情况，所以可以直接用f [i - 1 , j ]。10同理
对于01：
f [i - 1 , j ]
对于10：
f [ i , j - 1 ]

最后补充：

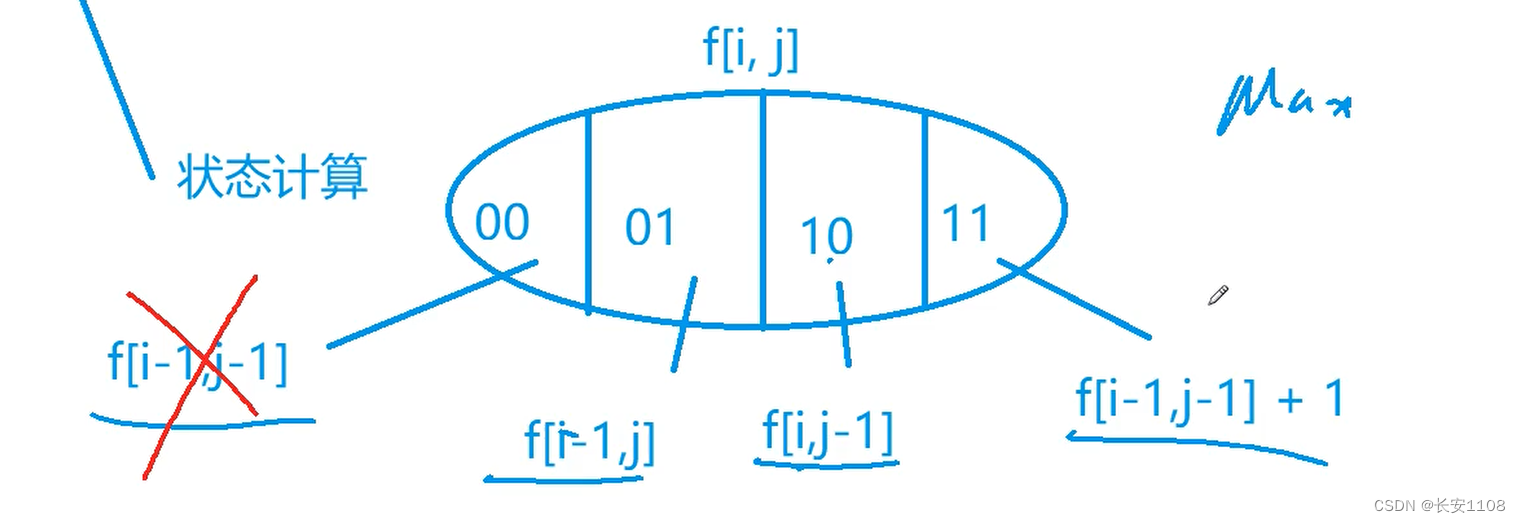
我们在写代码时，不用写00的情况，因为这种情况也被包含在了f [i - 1 , j ]和f [i , j - 1]两种情况里，所以我们在写代码时只需要考虑后面三种情况即可

例题+代码

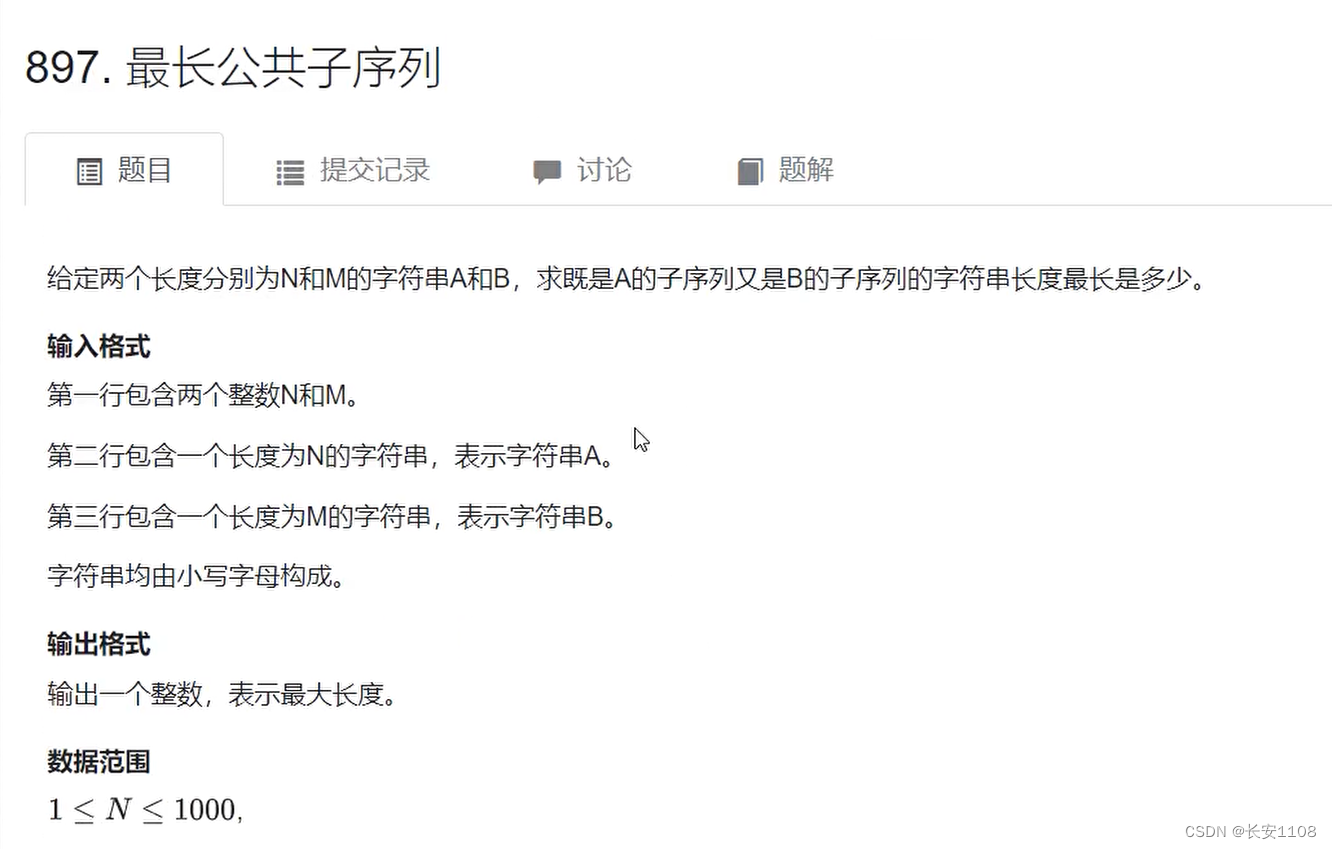
n和m表示a和b字符串的长度
char a b数组用来存储字符串
f数组是状态表示

之后在main里：
首先输入n 和 m
之后输入字符串，使用%s，以及数组名(这里是数组名+1，可以从数组的第二个位置，也就是下标为1的位置开始将整个字符串都读入,因为代码中出现了i-1)
之后for i 从1~=n
二重循环 j 从1~=m（也就是将所有的 f 进行了遍历）
f[i][j] = max (f[i-1][j] , f[i][j-1])，先将这两个进行取max
之后对11这种情况进行判断
只有当a[i] == b[j]时，才会有第三种情况，所以只有该条件成立，将第三种情况放入max中
最后输出 f[n][m]