我们先来看几个比较简单的例子来引入:

我们令f[i]表示以i为根节点的子树大小,易得状态转移方程为:
f[i]=1+f[son1]+....+f[soni];
我们用DFS即可,下面是大致的模板:

让我们来看看几道题吧:
1.贪心+树形DP+DFS:
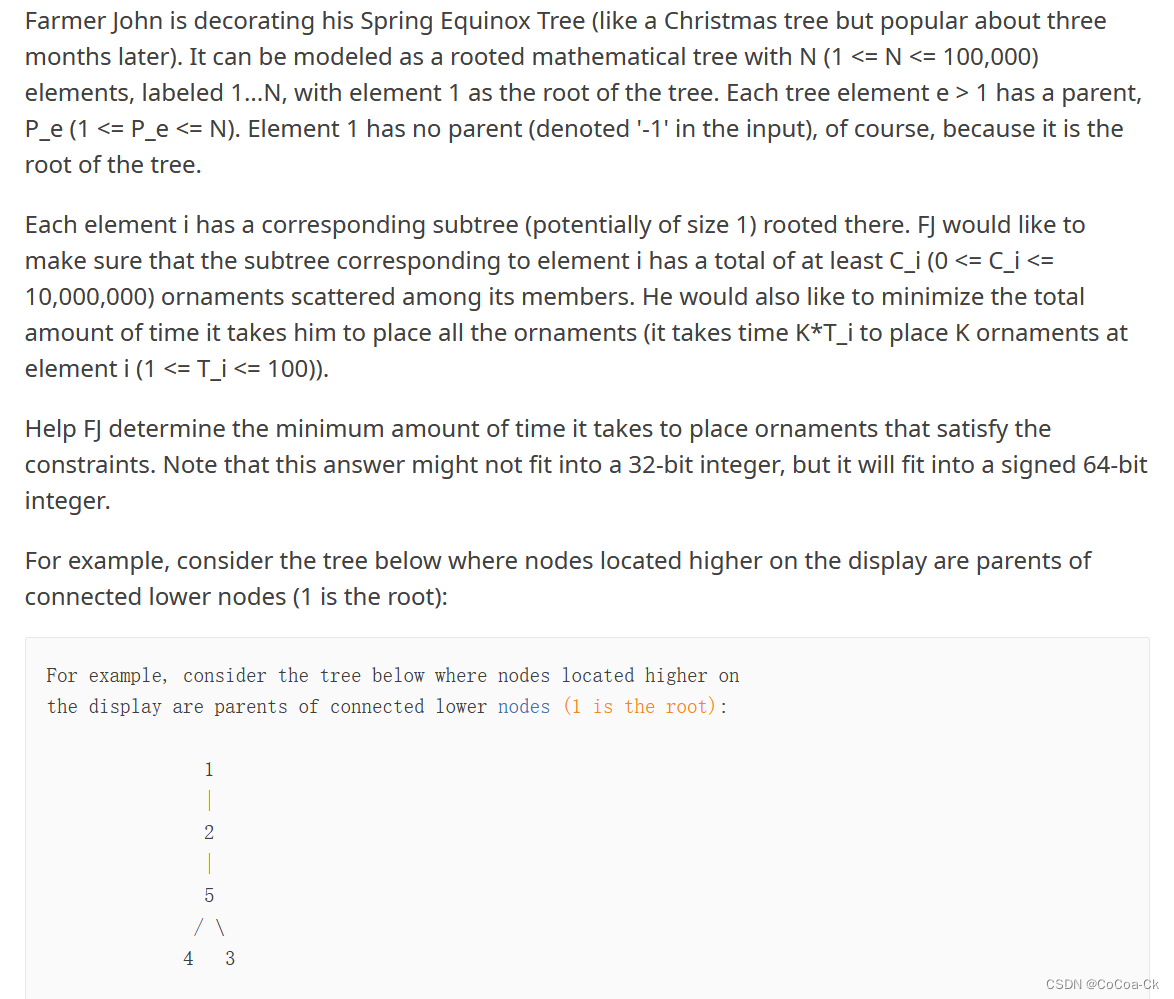

对于叶子节点,它要多少就弄多少,然后我们再分析它的父亲节点,假如它的子树还缺,那么就选其子树上最小的值即可。
因此,我们维护好每一个子树的min,然后再DFS一下各个子树所需的数量即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,t[100010],head[100010],cnt,p,root,min1[100010];
long long sum=0,c[100010];
struct node{
int dian,next;
}edge[100010];
void merge(int x,int y){
edge[++cnt].dian=y;
edge[cnt].next=head[x];
head[x]=cnt;
}
int dfsmin(int root){
if(head[root]==-1){
min1[root]=t[root];
return t[root];
}
min1[root]=t[root];
for(int i=head[root];i!=-1;i=edge[i].next){
min1[root]=min(dfsmin(edge[i].dian),min1[root]);
}
return min1[root];
}
long long dfssum(int root){
if(head[root]==-1){
sum+=c[root]*min1[root];
return c[root];
}
long long ckck=0;
for(int i=head[root];i!=-1;i=edge[i].next){
ckck+=dfssum(edge[i].dian);
}
if(ckck<c[root]){
sum+=(c[root]-ckck)*min1[root];
ckck=c[root];
}
return ckck;
}
int main(){
memset(head,-1,sizeof(head));
cin>>n;
for(int i=1;i<=n;i++){
scanf("%d%d%d",&p,&c[i],&t[i]);
if(p==-1){
root=i;
continue;
}
merge(p,i);
}
dfsmin(root);
dfssum(root);
cout<<sum;
} 接题:

我们要求的即为一个点,当他删去后要让形成的树中节点最多的尽量小。
我们考虑一个点删去,它的儿子形成树,它的父亲节点以上也形成了树。
于是,我们令f[i]为删去i后最大联通快的大小,
f[i]=max(tot[k],n-tot[i]),tot为树的大小,用树形dp维护即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,head[1010],x,y,cnt,sum[1010],inc[1010],root,f[1010];
struct node{
int dian,next;
}edge[1005];
void merge(int x,int y){
edge[++cnt].dian=y;
edge[cnt].next=head[x];
head[x]=cnt;
}
int dfssum(int root){
if(head[root]==-1){
return sum[root]=1;
}
sum[root]=1;
for(int i=head[root];i!=-1;i=edge[i].next){
sum[root]+=dfssum(edge[i].dian);
}
return sum[root];
}
int main(){
cin>>n;
memset(head,-1,sizeof(head));
for(int i=1;i<=n-1;i++){
cin>>x>>y;
merge(x,y);
inc[y]++;
}
for(int i=1;i<=n;i++){
if(inc[i]==0){
root=i;
break;
}
}
dfssum(root);
int ans=1000000,ans1,jj;
for(int i=1;i<=n;i++){
int ckck=-1;
for(int j=head[i];j!=-1;j=edge[j].next){
ckck=max(ckck,sum[edge[j].dian]);
}
ans1=max(ckck,n-sum[i]);
if(ans1<ans){
ans=ans1;
jj=i;
}
}
cout<<jj<<" "<<ans;
}接题:

我们令f[i][0]表示i节点不选时它和它的子树快乐最大指数,f[i][1]表示i节点选时它和它的子树快乐最大指数,因此,我们得到状态转移方程为:
f[i][0]=max(f[j][0],f[j][1])
f[i][1]=hi+
f[ri][0]=0,f[ri][1]=hri(ri为叶子节点)
结果就是max(f[root][0],f[root][1]).
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,head[6010],cnt,inc[6010],x,y,root,dp[6010][2],h[6010],pos[6010][2];
struct node{
int dian,next;
}edge[6010];
void merge(int x,int y){
edge[++cnt].dian=y;
edge[cnt].next=head[x];
head[x]=cnt;
}
int dfs(int root,int k){
if(pos[root][k]==1) return dp[root][k];
if(k==1){
dp[root][k]=h[root];
for(int i=head[root];i!=-1;i=edge[i].next){
dp[root][k]+=dfs(edge[i].dian,0);
}
}
else{
for(int i=head[root];i!=-1;i=edge[i].next){
dp[root][k]+=max(dfs(edge[i].dian,0),dfs(edge[i].dian,1));
}
}
pos[root][k]=1;
return dp[root][k];
}
int main(){
memset(head,-1,sizeof(head));
cin>>n;
for(int i=1;i<=n;i++) cin>>h[i];
for(int i=1;i<=n-1;i++){
cin>>x>>y;
merge(y,x);
inc[x]++;
}
cin>>x>>y;
for(int i=1;i<=n;i++){
if(inc[i]==0){
root=i;
break;
}
}
int jj=dfs(root,1);
int gg=dfs(root,0);
cout<<max(jj,gg);
}