目录
一、什么是递归
1.1.递归的思想
1.2.递归的限制条件
二、举例体会
2.1.求n的阶乘
2.2.顺序打印整数的每一位
2.3.斐波那契数列
三、递归与迭代
一、什么是递归
在学习C语言的过程中,我们经常会跟递归打交道,什么是递归呢?它其实是一种解决问题的方法,递归递归,顾名思义,递推和回归。在C语言中,函数自己调用自己就是递归,我们可以把它想成生活中的俄罗斯套娃。
下面请看最简单的递归代码:
#include <stdio.h>
int main()
{
printf("hehe\n");
main();//main函数中⼜调⽤了main函数
return 0;
}在上面的代码中,我们看到了main函数里再次调用了main函数,我们可以想象,这个程序会一直调用下去,直到,内存不够导致栈溢出(Stack overflow)。
1.1.递归的思想
递归的思想用一个词来讲就是“大事化小”。
其中递代表递推,归代表回归。
1.2.递归的限制条件
刚刚我们看到,一直调用main函数的话,会造成死递归,因此,我们在使用递归时需要注意一些必要条件。
1.递归存在限制条件,当超过这个限制条件时递归就应该停止
2.每次递归应该越来越接近这个限制条件。
接下来我们举几个例子来让大家体会一下这两个必要条件。
二、举例体会
2.1.求n的阶乘
⼀个正整数的阶乘(factorial)是所有⼩于及等于该数的正整数的积,并且0的阶乘为1。自然数n的阶乘写作 n! 。
经分析可知n! = n * (n-1) * (n-2)... * 3 * 2 * 1,而(n-1)! = (n-1) * (n-2) *...* 3 * 2 * 1。
所以n! = n * (n-1)!。
我们要求n的阶乘,只需要求n和n-1的阶乘的乘积,问题也就变成了求n-1的阶乘。经过一次递归,我们就从n变到n-1,那递归的次数足够了,我们就可以到最后的1的阶乘。那怎么得到n的阶乘呢,我们刚刚一步一步得到1的阶乘,那我们再一步一步乘回去,最终得到n的阶乘。
上述思路就是所谓的递归,也就是把一个较大的问题转换为与原问题相似的小问题。
当n = 0时,n! = 1。我们可以得到递推公式:
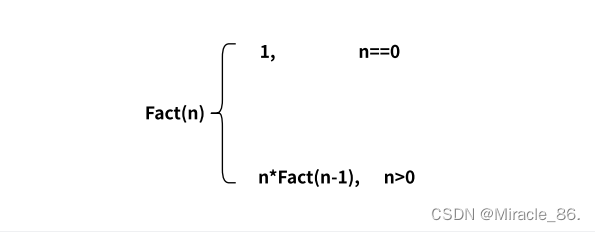
代码如下:
函数部分
int Fact(int n)
{
if(n==0)
return 1;
else
return n*Fact(n-1);
}总体
#include <stdio.h>
int Fact(int n)
{
if(n==0)
return 1;
else
return n*Fact(n-1);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fact(n);
printf("%d\n", ret);
return 0;
}测试结果

2.2.顺序打印整数的每一位
输入一个整数n,顺序打印其每一位。
input : 1234
output : 1 2 3 4
分析可知,1234/10 = 123,而1234%10 = 4。那我们可以巧妙的利用上述特性,得到1234的每一位。但是出现一个问题,我们获得的数字的顺序是倒着的,这该怎么办呢。我们可以仔细品味一下递归,递推和回归,先递推再回归。
我们就可以先进行/10的操作,再打印%10的余数,如下:
void Print(int n)
{
if(n>9)
{
Print(n/10);
}
printf("%d ", n%10);
}画图推演一下:
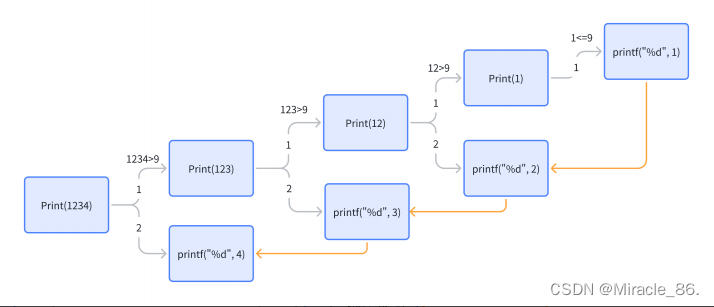
代码如下:
#include<stdio.h>
void Print(int n)
{
if (n > 9)
{
Print(n / 10);
}
printf("%d ", n % 10);
}
int main()
{
int m = 0;
scanf("%d", &m);
Print(m);
return 0;
}运行结果:
2.3.斐波那契数列
斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称“兔子数列”,其数值为:1、1、2、3、5、8、13、21、34……
其递推公式为
![]()
用递推写出代码很简单:
#include<stdio.h>
int Fib(int n)
{
if (n == 1 || n == 2)
return 1;
else
return Fib(n - 1) + Fib(n - 2);
}
int main()
{
int n = 0;
scanf("%d", &n);
printf("%d", Fib(n));
return 0;
}运行结果:
那如果让你不用递归的方法,你会怎么做呢?
我们可以创建三个变量,就像两个数互相交换那样,将a赋值1,b赋值1,c为a与b的和。
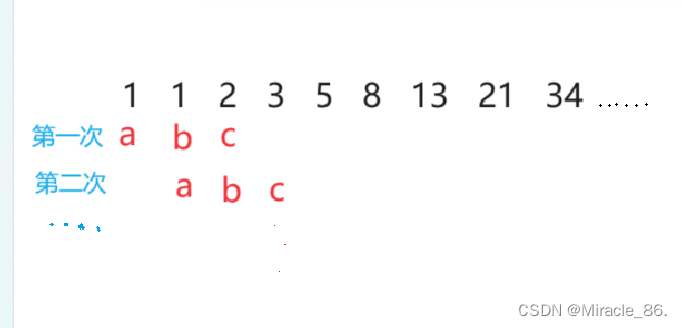
n大于二之后才开始循环,所以我们可以这么写:
int Fib(int n)
{
int a = 1, b = 1,c = 0;
while (n>2)
{
c = a + b;
a = b;
b = c;
n--;
}
return b;
}一个接着一个交换值,直到n等于2,退出循环,此时c的值赋给了b,而我们在n小于等于2的时候,求不出来c,而b的值正好是1,所以我们返回b的值。
三、递归与迭代
上面我们说了什么是递归,这又来个迭代,什么叫迭代呢?说白了通常就是循环。
比如刚才计算阶乘,我就不想用递归,那我就循环n次,也可以解决问题,并且该方法效率比递归高。
我们遇到的许多问题用递归解释的原因是因为,它比非递归好想好解释,但这些问题往往迭代比递归的效率更高。
我们说当一个问题非常复杂,难以用迭代的方式来解决时2,这时候递归实现的简洁性便可以补偿运行时的开销。
就像刚刚的例三,求斐波那契数列,使用迭代的方法就更加有效率。
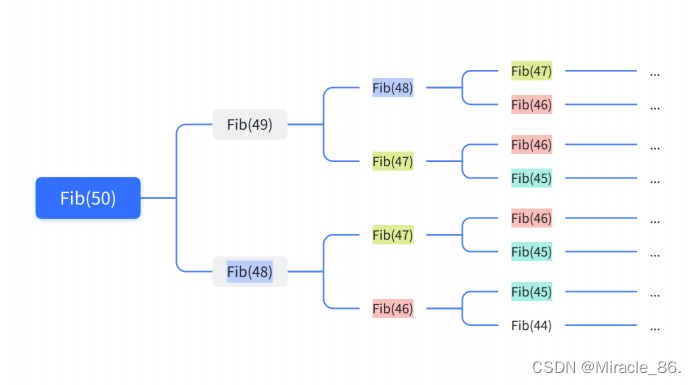
如图所示,递归层次越深,冗余计算越多,我们可以简单测试一下
#include <stdio.h>
int count = 0;
int Fib(int n)
{
if(n == 3)
count++;//统计第3个斐波那契数被计算的次数
if(n<=2)
return 1;
else
return Fib(n-1)+Fib(n-2);
}
int main()
{
int n = 0;
scanf("%d", &n);
int ret = Fib(n);
printf("%d\n", ret);
printf("\ncount = %d\n", count);
return 0;
}来看结果

这才是40,可想而知50会是多大的天文数字。
而迭代的方式,我们只需要前后一步一步相加即可。
最后总结一下,递归是一个很好的解决问题方式,在编程学习中,我们会经常用到它,但是它也不是万能的,还是需要我们多动脑思考。
我相信,我们总会找到解决办法的。