这里写目录标题
- 区间问题
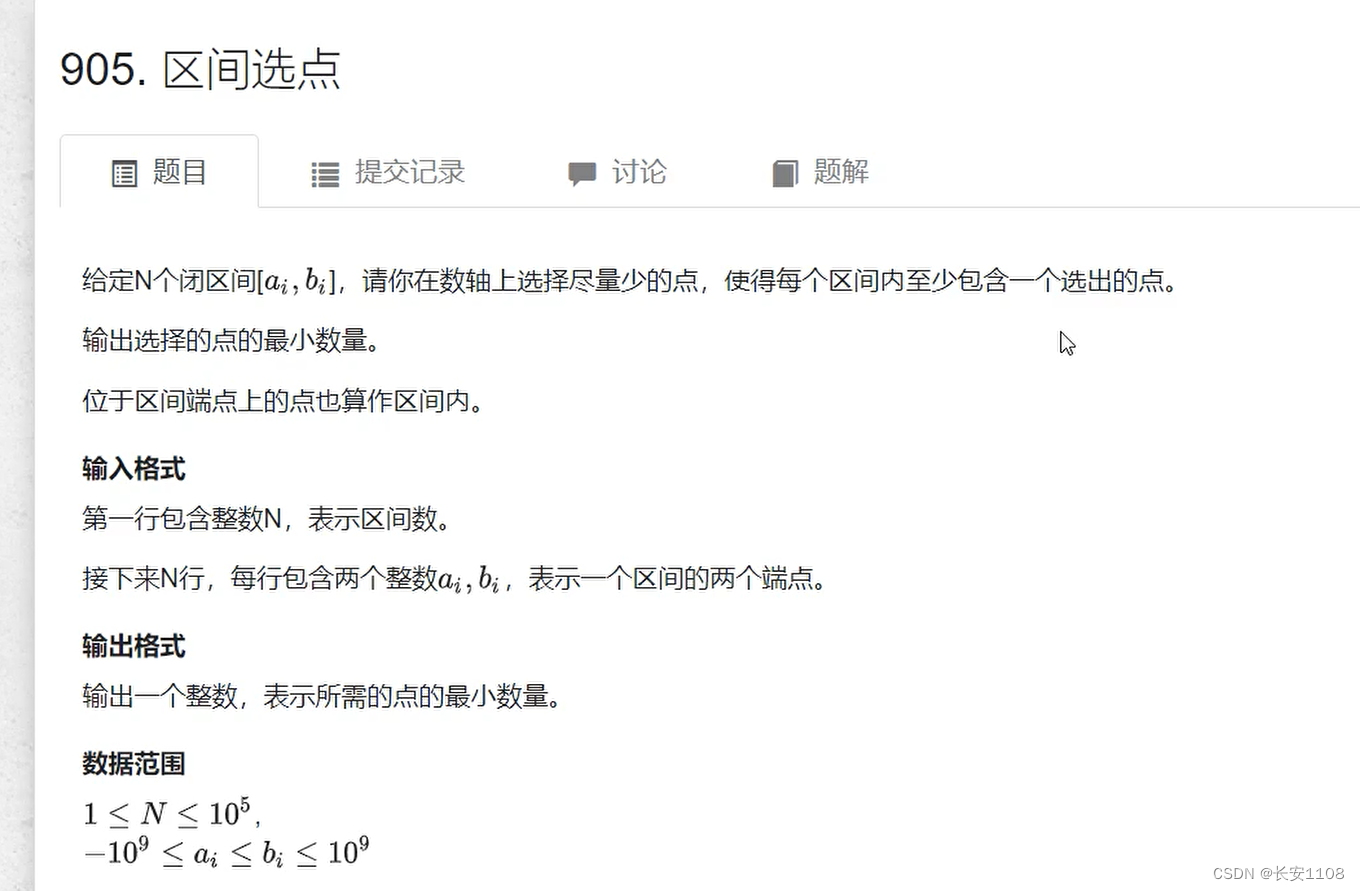
- 区间选点
- 引入
- 算法思想
- 例题+代码
- 最大不相交区间的数量
- 算法思想
- 例题+代码
- 区间分组
- 算法思想
- 例题+代码
- 一级目录
- 二级目录
- 二级目录
- 二级目录
区间问题
区间选点
引入
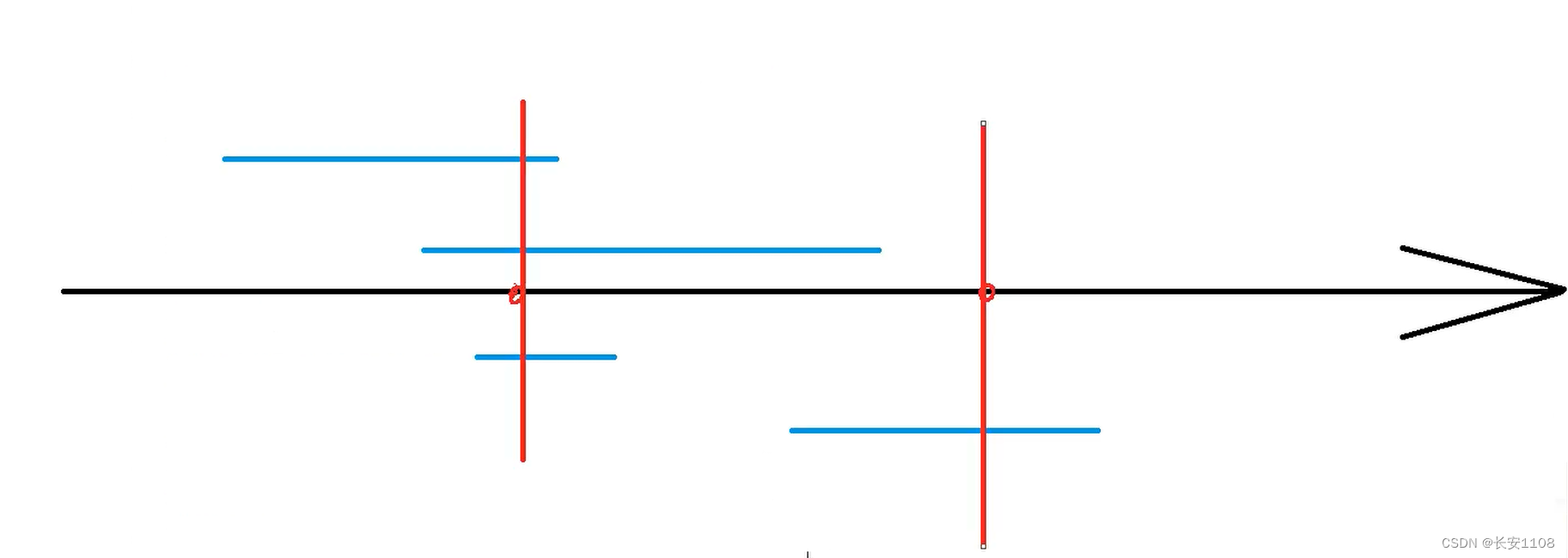
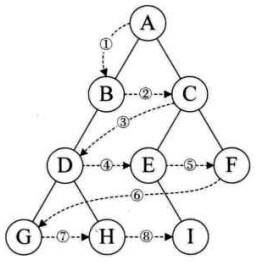
区间问题会给定几个区间,之后要求我们在数轴上选取尽量少的点,使得每个区间内至少包含一个选出的点,如上图,对于这四个区间,我们选择两个点,就可以满足条件
算法思想

贪心算法使用场景:问题是单峰问题,即他的极值就是最值
基本思路:
对于一个贪心问题,我们没有固定的模版,一般的做法是,我们选出一小块示例,在该示例里面进行推演,推演时按照最理想的解法进行推算,进行尝试,如果在当前这一小部分的实例里是最优解,那么大概率在整个题目中都是最优解,有了初步的推演之后,我们就可以对推演进行正确性的证明。
例如,上图中,
推演的算法是:先将每个区间右端点进行从小到大排序,之后从前往后依次枚举每个区间,如果当前区间内有已经有点,直接pass,如果没有,则选择当前区间的右端点,这样,这段算法在当前部分是合法的
之后进行证明

我们利用这样的等价原理(如上图)进行证明,
ans是在整个题目中的最优解,cnt是当前推演的算法的解(对于本题而言,解就是点的个数)
首先,对于第一点,由于我们的算法,是合法的,所以,我们的算法主要最次也就是点数比ans要多,因为ans是最优解,所以有ans <= cnt
之后,对于第二点,要证明ans >= cnt ,那么就要证明ans >= cnt的最大值,而cnt的最大值就是所有的区间都没有重复点(如下图),那么根据我们的推演算法,每个区间都要选中一点,且每个区间有且只选一点,那么在这种产生最大值的区间排列情况下,我们的推演算法是最小值,所以,ans 只能 >= ant
(补充:对于该条件,我们可以这样想:只要cnt在“区间排列产出的值是N”这个情况下,仍然合法,cnt的值是N,那么一定有ans >= cnt)
进而证明了 ans == cnt

例题+代码

首先定义了一个结构体,来存储区间
结构体内;
定义 l ,r。分别表示左端点和右端点
之后重载小于号:
bool operator< (const Range &W)const
{
return r < W.r;
}
这个重载放在结构体里面,相当于成员函数,那么该重载只会用在结构体类型变量的小于比较之间,表示一个结构体变量操作数进行“<”操作时,会将与“<”后面的结构体变量传入该重载函数,而操作“<”的结构体变量就是重载函数的this变量
最后结构体后面加了个range[N],表示前面定义结构体的一大坨是一个变量类型,表示是结构体变量类型的数组,相当于 int a;
在main函数中,首先输入n对数据,
这里注意,结构体变量赋值时,使用大括号+逗号进行赋值
之后调用sort函数,对结构体数组里面的变量进行排序,这里是结构体变量排序,会用到结构体定义时的小于号重载
排完序后,定义res=0,用来存储答案,ed=-2e9,-2e9表示负无穷,ed是用来表示当前所选中的点,(注意,当前所选中的点只会保留最新的点,其他点如果被刷下去,会用res++存储,所以是合理的)
之后for循环,对于右端点从小到大的每个区间,我们依次判断情况
直接进行判断 if(range[i].l > ed)如果大于,那么就是区间内没有选中点的情况,那么就记录旧点,更新新点
res++;
ed = range[i].r
其他情况已经包含在内(刚开始第一个区间,肯定会进入到if里面,所以第一个区间的右端点一定有点,之后的区间,如果有,则跳过进行下一个区间的判断,如果没有,进入到if函数里面)
最大不相交区间的数量
算法思想

我们仍然可以利用上一题的推演,该推演对于本题仍然适用,
进行推演:
对于本题,我们可以将上一题稍作变化,上一题是重合的区间只选一个点,现在我们不选点,重合的区间除去第一个区间以外,其他的都pass,扔掉,而不重合的区间,直接选中该区间的右端点,同时记录该区间选中,这样从小到大进行选择,一定会选出最大数量的区间数
之后进行证明:
仍然是上一题的证明原理,显而易见,我们可以直接整除第二点:因为我们的cnt算法是合法的,而ans算法不仅合法,且是最大值,所以cnt只能 <= ans,即ans >= cnt
而对于第一点,因为cnt算法(即我们自己的推演算法)会保证不重合的区间都计数,所以当N个区间都不重合,那此时cnt算法的值就是N,已经是最大的数量了,因为只有N个区间,而ans、cnt都是合法的,所以,ans只能 <= cnt
(补充:对于该条件,我们可以这样想:只要cnt在“区间排列产出的值是N”这个情况下,仍然合法,cnt的值是N,那么一定有ans >= cnt)
所以,综上,ans == cnt

例题+代码


代码与上题完全一样,上题是记录点的个数,这题是记录区间的个数,而点的个数对应着区间个数,所以代码一样
区间分组
算法思想


首先,将所有的区间按左端点从小到大排序
之后,从前往后处理每个区间:
判断能否将其放到某个现有的组中,能放入的条件是:L[ i ] > Max_r(Max_r就是一个组中最新加入的区间的右端点,每次加入新的区间,把Max_r更新一下即可)
对于判断的结果进行讨论:
1.如果不存在这样的组,那么就是所有的组都不满足,那开一个新组,放入该区间
2.如果存在这样的组,将其放进去,并更新当前组的Max_r
证明其正确性:

同样的,我们需要证明这两点,
首先对于第一点,因为我们的cnt是合法的,而答案ans不仅合法,还是最小值,所有只能有 ans <= cnt
对于第二点,我们可以这样想:只要cnt在“区间排列产出的值是N”这个情况下,仍然合法,那么一定有ans >= cnt,换句话说,判断另一个难以判断的条件时,只要有cnt=N这种情况可以出现,那么我们的推演算法就是合法的
所以,依据这个原理,我们设置所有的区间都是互相重合的,那么就需要分N个组,如果在这种情况下,我们的推演算法的值cnt==N,那么该条件成立,根据推演第一条,“不存在这样的组之后,就新开一个组”,所以会开N个组,所以,第二个条件成立
例题+代码


首先在定义结构体Range时,重载小于号时,用L进行重载,因为要用左端点进行排序
之后,main函数中,输入n个l,r
进行排序,(按照重载的小于号排序)
之后,priority_queue<int, vector, greater> heap;(这是小根堆的定义,小根堆是指堆中顶部是堆中所有数据的最小值)
之后,循环n次,
每次循环都拿出数组中的一个数据 r(这是一个Range类型的数据)
之后判断,当堆为空 || heap.top() >= r.l ,(之所以使用top元素进行判断,是因为要用各组的Max_r中最小的一个进行比较,这样如果还是重合,那就新开一个组)那么就新开一个组(表现在代码上就是往栈中推一个右端点)
else {
int t = heap.top(),这一步在该题没啥用,但是可以拿出来堆顶元素,可能其他题会有用
heap.pop(),删除堆顶元素
heap.push(r.r),将新加入的区间的右端点推入堆中
(上面两行代码,缺一不可,删一个加一个,实际上就是实现了更新一个组的Max_r,因为堆中一个元素就代表一个组,元素的值是改组的最右端点)
}