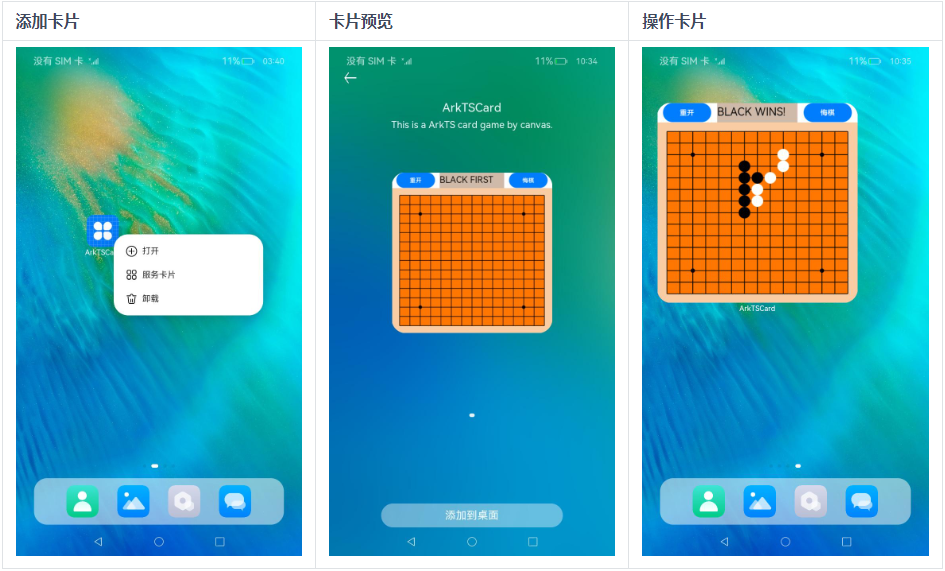
01背包问题：组合问题

题目

思路

将nums数组分成left和right两组，分别表示相加和相减的两部分，则：

• left - right = target
• left + right = sum

进而得到left为确定数如下，且left必须为整数，小数表示组合不存在：

• left = (target + sum)/2

所以问题转化为寻找$left=(target+sum)/2$的所有组合。
设$left$为背包最大容量，则$dp[left]$表示装满背包的组合(路径)数

有哪些来源可以推出dp[j]呢？
只要搞到nums[i]，凑成dp[j]就有dp[j - nums[i]] 种方法。 例如：dp[j]，j为5，
已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 容量为5的背包。
已经有一个2（nums[i]） 的话，有dp[3]种方法 凑成 容量为5的背包。
已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 容量为5的背包
已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 容量为5的背包
已经有一个5 （nums[i]）的话，有 dp[0]中方法凑成容量为5的背包
那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。
dp[j] += dp[j - nums[i]]

而01背包求组合数的方法总结为：

初 始 化：dp[0] = 1 ，其他为零
递推函数：dp[j] += dp[j - nums[i]] (物品重量 ≤ j ≤ 背包容量)
for 循 环：遍历背包容量依旧倒序

代码

二维数组（易于理解）

class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        total_sum = sum(nums)  # 计算nums的总和
        if abs(target) > total_sum:
            return 0  # 此时没有方案
        if (target + total_sum) % 2 == 1:
            return 0  # 此时没有方案
        target_sum = (target + total_sum) // 2  # 目标和

        # 创建二维动态规划数组，行表示选取的元素数量，列表示累加和
        dp = [[0] * (target_sum + 1) for _ in range(len(nums) + 1)]

        # 初始化状态
        dp[0][0] = 1

        # 动态规划过程
        for i in range(1, len(nums) + 1):
            for j in range(target_sum + 1):
                dp[i][j] = dp[i - 1][j]  # 不选取当前元素
                if j >= nums[i - 1]:
                    dp[i][j] += dp[i - 1][j - nums[i - 1]]  # 选取当前元素

        return dp[len(nums)][target_sum]  # 返回达到目标和的方案数

一维数组（简洁）

class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        total_sum = sum(nums)  # 计算nums的总和
        if abs(target) > total_sum:
            return 0  # 此时没有方案
        if (target + total_sum) % 2 == 1:
            return 0  # 此时没有方案
        left = (target + total_sum) // 2  # 目标和
        dp = [0] * (left + 1)  # 创建动态规划数组，初始化为0
        dp[0] = 1  # 当目标和为0时，只有一种方案，即什么都不选
        for i in range(len(nums)):
            for j in range(left, nums[i] - 1, -1):  # 依旧倒序
                dp[j] += dp[j - nums[i]]  # 状态转移方程，累加不同选择方式的数量
        return dp[left]  # 返回达到目标和的方案数

回溯法（超时）

class Solution:
    def backtracking(self, candidates, target, total, startIndex, path, result):
        if total == target:
            result.append(path[:])  # 将当前路径的副本添加到结果中
        # 如果 sum + candidates[i] > target，则停止遍历
        for i in range(startIndex, len(candidates)):
            if total + candidates[i] > target:
                break
            total += candidates[i]
            path.append(candidates[i])
            self.backtracking(candidates, target, total, i + 1, path, result)
            total -= candidates[i]
            path.pop()

    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        total = sum(nums)
        if target > total:
            return 0  # 此时没有方案
        if (target + total) % 2 != 0:
            return 0  # 此时没有方案，两个整数相加时要注意数值溢出的问题
        bagSize = (target + total) // 2  # 转化为组合总和问题，bagSize就是目标和

        # 以下是回溯法代码
        result = []
        nums.sort()  # 需要对nums进行排序
        self.backtracking(nums, bagSize, 0, 0, [], result)
        return len(result)