神经网络系列---感知机(Neuron)

文章目录

- 感知机(Neuron)
- - 感知机(Neuron)的决策函数可以表示为：
  - 感知机(Neuron)的学习算法主要包括以下步骤：
  - 感知机可以实现逻辑运算中的AND、OR、NOT和异或(XOR)运算。

感知机(Neuron)

感知机(Neuron)是一种简单而有效的二分类算法，用于将输入数据划分为两个类别。它是机器学习中最早的分类算法之一，由罗森布拉特（Rosenblatt）在1957年提出。

感知机(Neuron)的基本思想是通过一个决策函数将输入数据映射到特定的输出类别。它通过对输入向量进行加权求和，并将结果传递给一个激活函数来产生输出。感知机(Neuron)的学习过程主要涉及确定合适的权重，以便对不同的输入样本进行正确的分类。

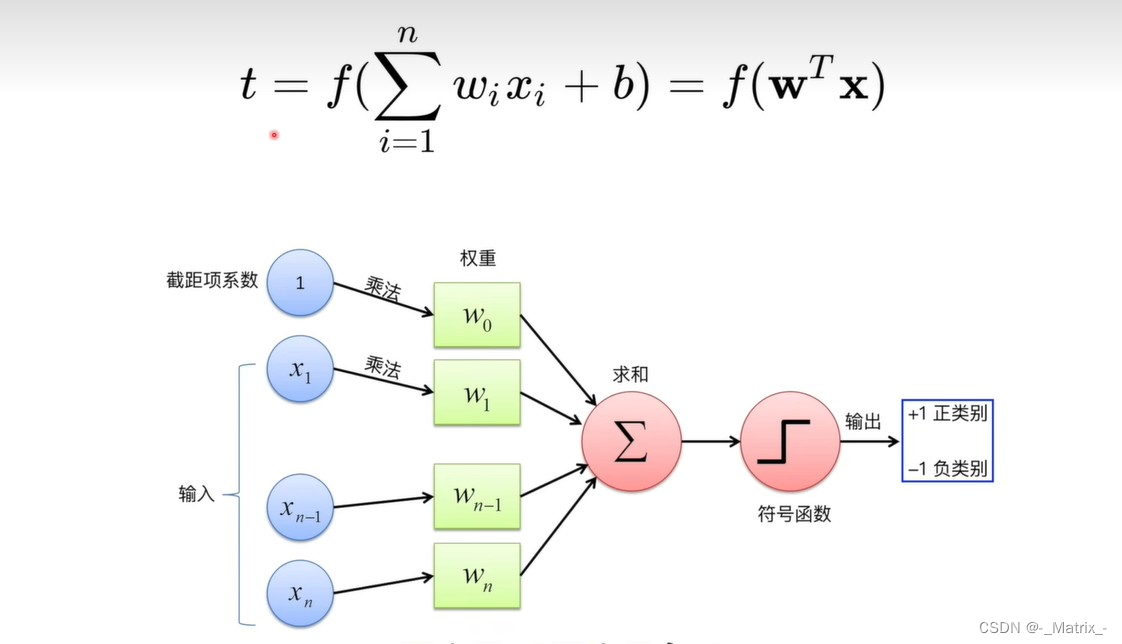
在这里插入图片描述

感知机(Neuron)的决策函数可以表示为：

    f(x) = sign(w * x + b)

    sign(x) = {
    +1, if x >= 0,
    -1, if x < 0
    }

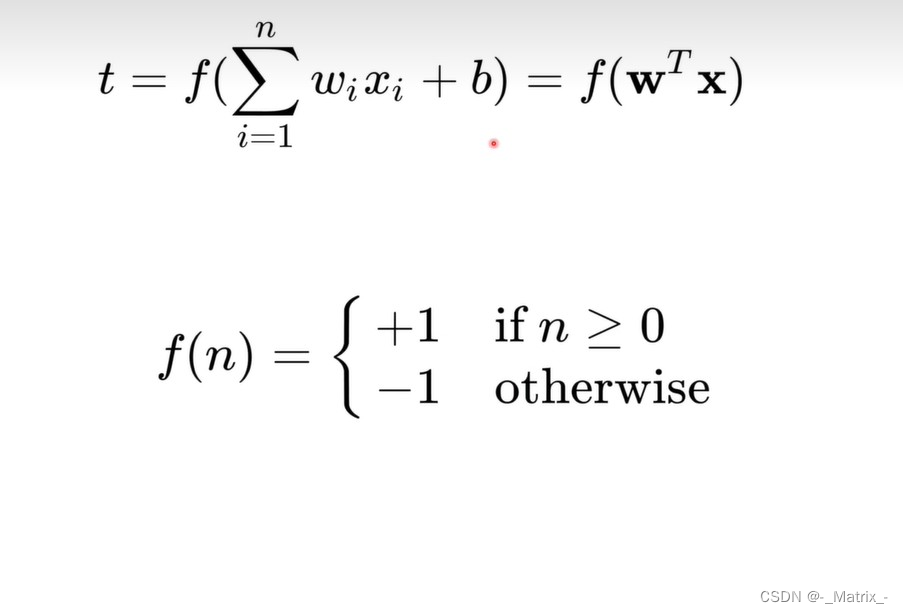
在这里插入图片描述

它将大于等于0的值映射为+1，小于0的值映射为-1。在感知机(Neuron)中，"sign"函数被用于判断输入的加权和是否超过了某个阈值，从而确定输入被分类为哪个类别。
其中，x是输入向量，w是权重向量，b是偏置项，sign是符号函数，将输入的实数映射为+1或-1，表示两个不同的类别。

感知机(Neuron)的学习算法主要包括以下步骤：

初始化权重向量和偏置项。
针对训练数据中的每个样本，计算决策函数的输出。
根据实际输出和期望输出之间的差异，更新权重向量和偏置项。
重复步骤2和步骤3，直到所有训练样本都被正确分类或达到停止条件。

需要注意的是，感知机(Neuron)只适用于线性可分的问题，即可以通过一个超平面将两个类别的数据完全分开。对于线性不可分的问题，感知机(Neuron)算法无法收敛。

虽然感知机(Neuron)算法在解决简单分类问题上很有用，但它对于复杂问题的处理能力有限。后续发展出了更多强大的分类算法，如支持向量机（Support Vector Machine）和神经网络（Neural Networks）。


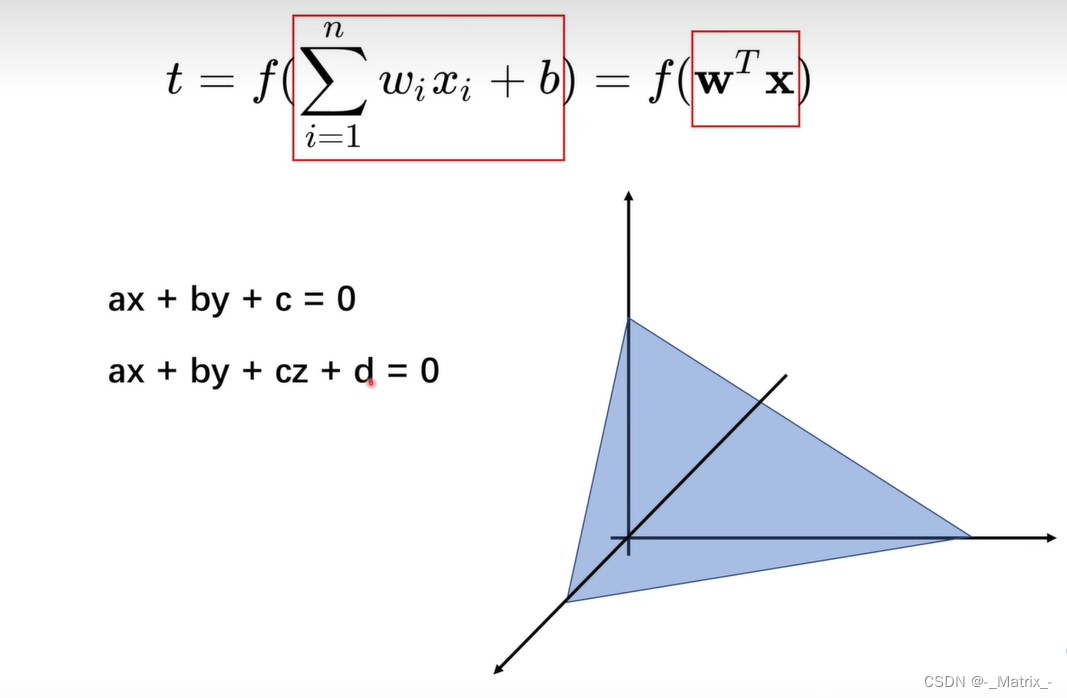
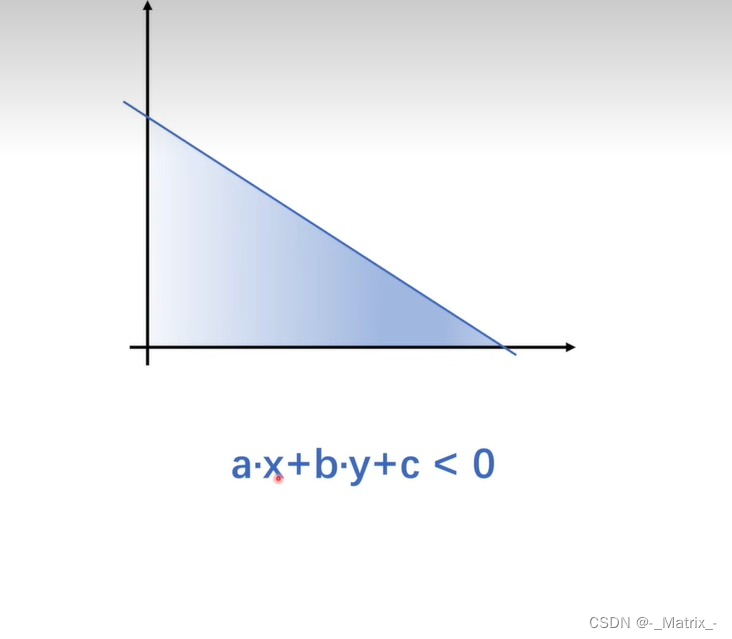
y=ax+c  ==> ax +(-y)+c =0  //表示一条线 一维形式

z=ax+by+d  ==> ax +by+(-z)+d =0  //表示一个平面 二维形式
类似于神经网络中的 权重和偏置

在这里插入图片描述

ax +by+c =0  //表示所有数据都在这一条线上

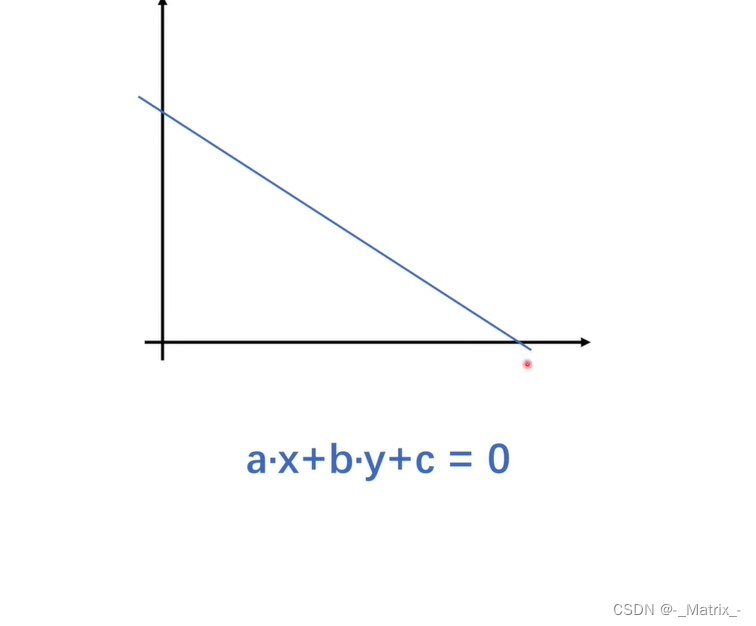
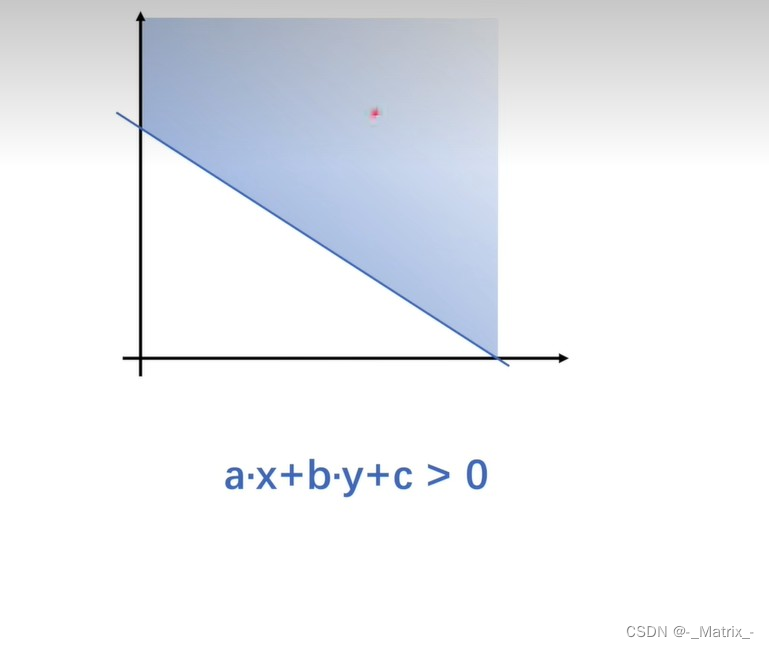
在这里插入图片描述

ax +by+c > 0  //表示所有数据都在这一条线的上方

在这里插入图片描述

ax +by+c < 0  //表示所有数据都在这一条线的上下方

在这里插入图片描述

多维度表示：相乘在相加

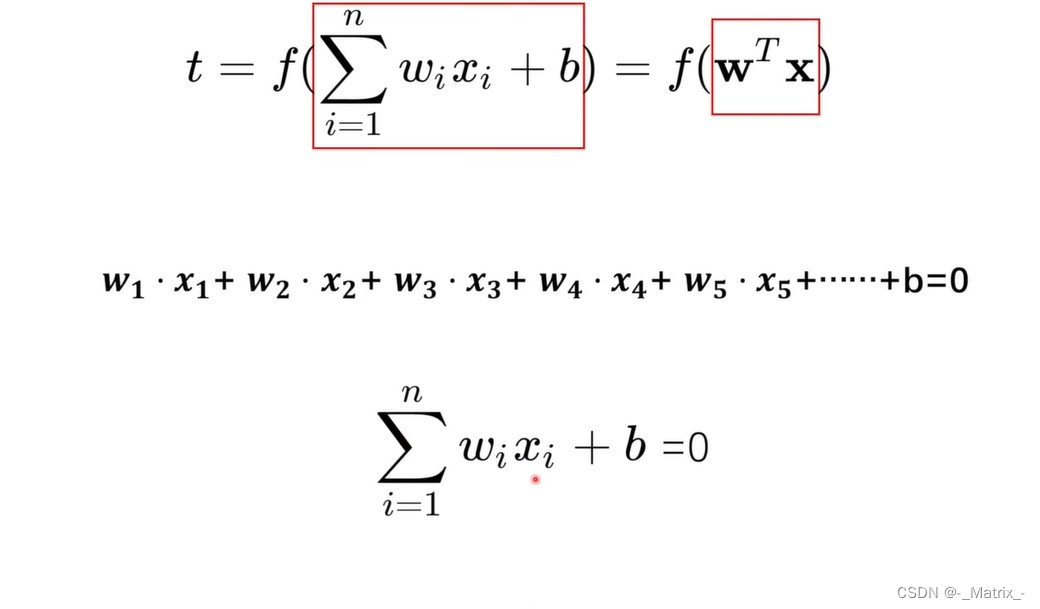
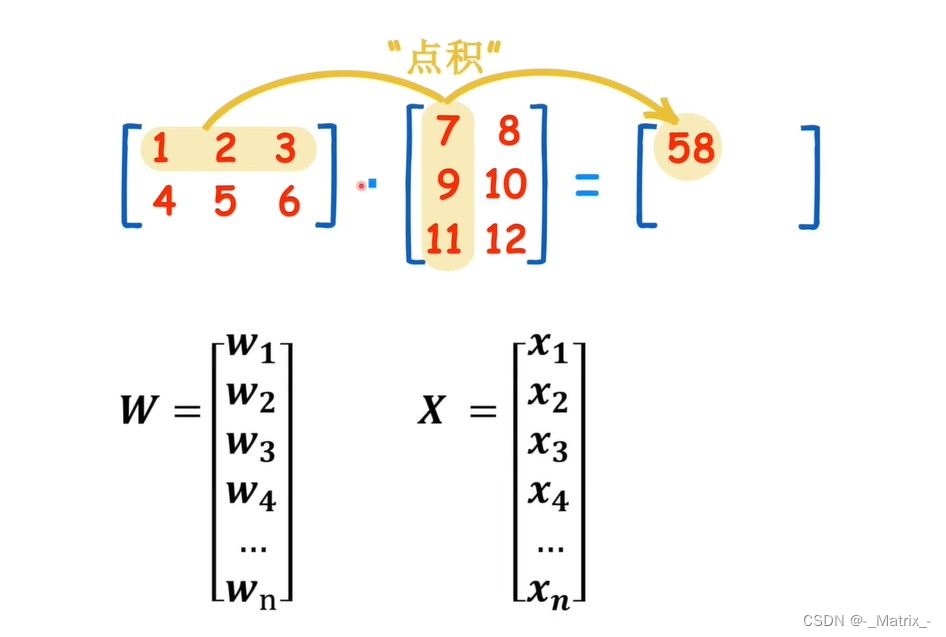
在这里插入图片描述

用矩阵表示

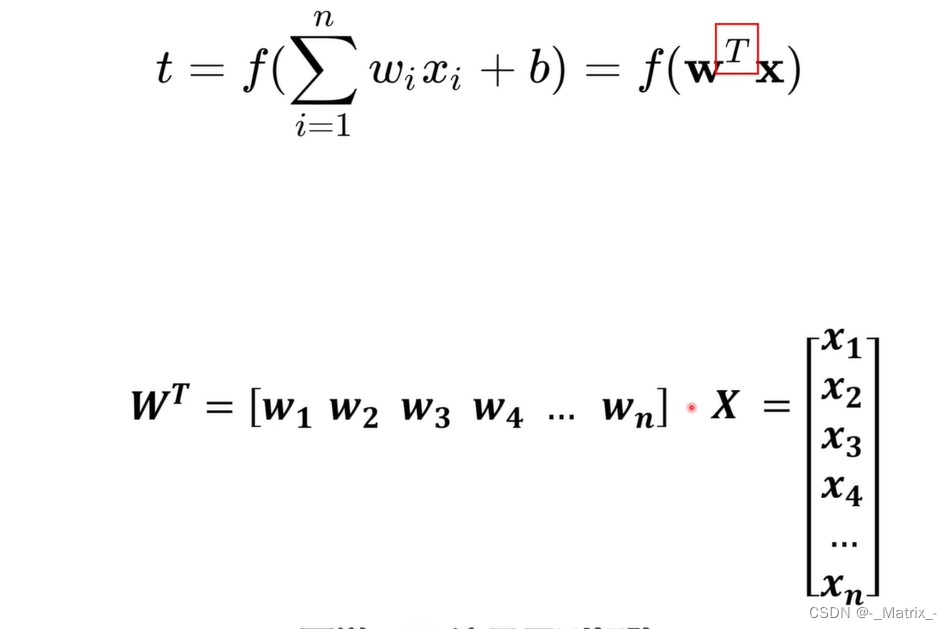
在这里插入图片描述

下面用感知机(Neuron) 表达与(AND)、或(OR) 、非(NOT) 、异或(XOR) 、运算。

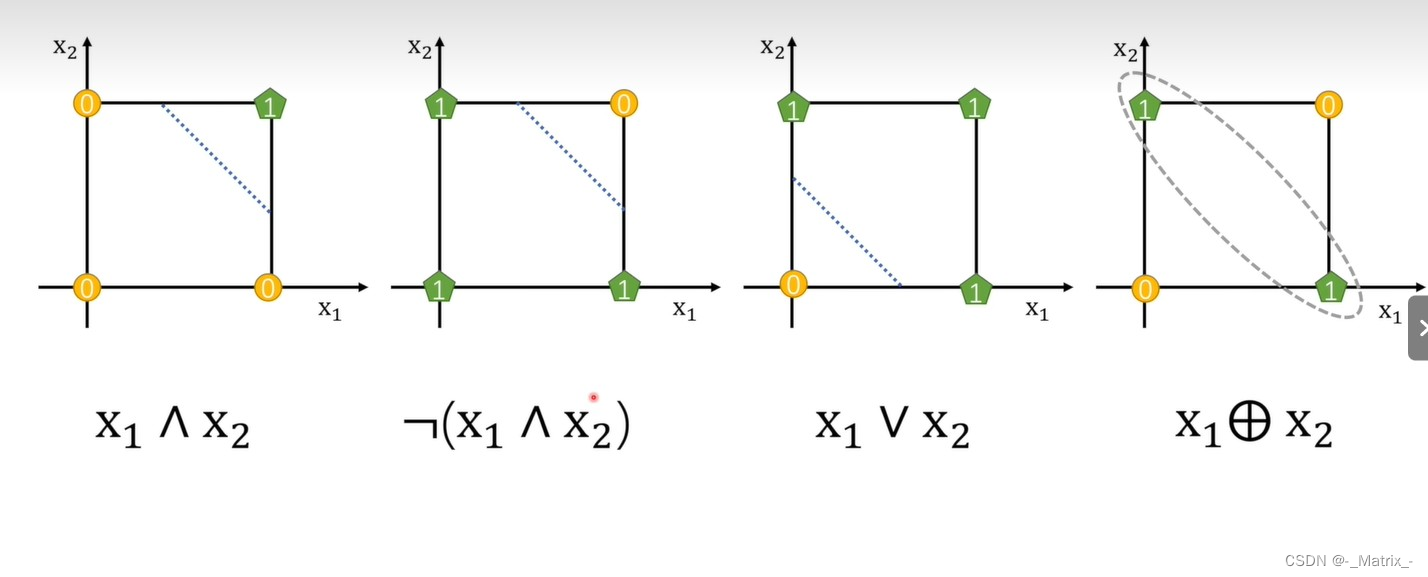
在这里插入图片描述

感知机可以实现逻辑运算中的AND、OR、NOT和异或(XOR)运算。

这里我将为你详细说明如何使用感知机实现这些逻辑运算。

AND运算：
AND运算是一个二元运算，当且仅当两个输入都为1时，输出为1，否则输出为0。使用感知机可以实现AND运算，具体步骤如下：

设置权重向量为 w = [1, 1]，偏置项为 b = -1.5。
对于输入向量 x = [x1, x2]，计算加权和：z = w * x + b。
使用符号函数（sign）作为激活函数，即 f(x) = sign(z)。也就是f(x) = sign(x1 + x2 - 1.5)，其中sign函数将大于等于0的值映射为1，小于0的值映射为-1。
当且仅当 f(x) = 1 时，表示 AND 运算结果为真，否则为假。

OR运算：
OR运算也是一个二元运算，当两个输入中至少一个为1时，输出为1，否则输出为0。使用感知机可以实现OR运算，具体步骤如下：

设置权重向量为 w = [1, 1]，偏置项为 b = -0.5。
对于输入向量 x = [x1, x2]，计算加权和：z = w * x + b。
使用符号函数（sign）作为激活函数，即 f(x) = sign(z)。也就是f(x) = sign(x1 + x2 - 0.5)，其中sign函数将大于等于0的值映射为1，小于0的值映射为-1。
当且仅当 f(x) = 1 时，表示 OR 运算结果为真，否则为假。

NOT运算：
NOT运算是一个一元运算，当输入为1时，输出为0，当输入为0时，输出为1。使用感知机可以实现NOT运算，具体步骤如下：

设置权重向量为 w = [-1]，偏置项为 b = 0.5。
对于输入 x，计算加权和：z = w * x + b。
使用符号函数（sign）作为激活函数，即 f(x) = sign(z)。也就是f(x) = sign( -x + 0.5)，其中sign函数将大于等于0的值映射为1，小于0的值映射为-1。
当且仅当 f(x) = 1 时，表示 NOT 运算结果为真，否则为假。

异或运算一个感知机无法实现

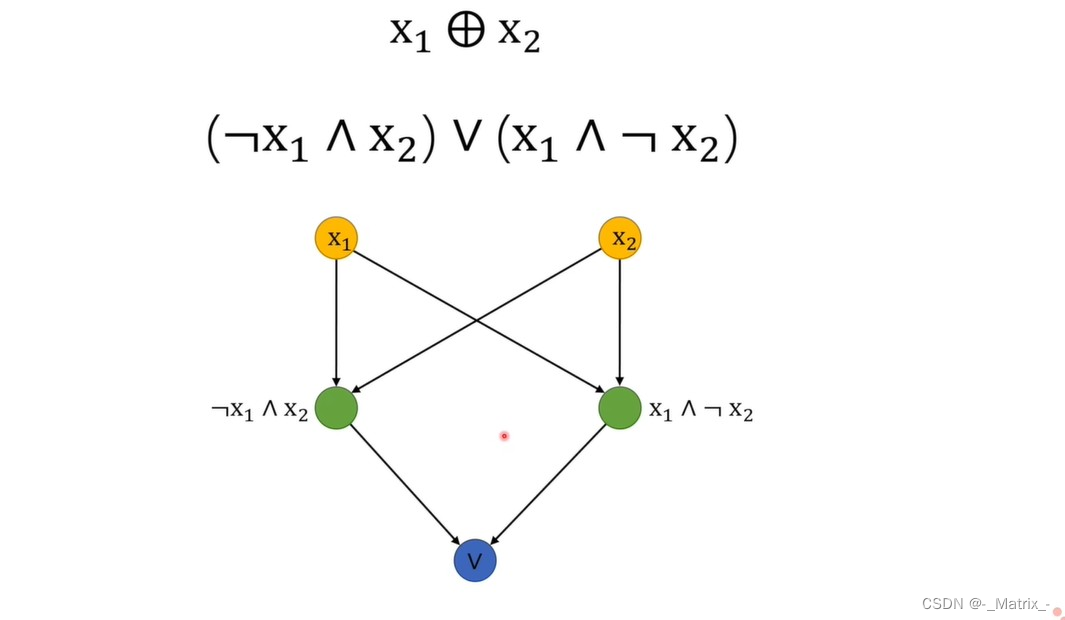
在这里插入图片描述

描述上图异或(XOR)运算：
异或运算是一个二元运算，当两个输入相同时，输出为0；当两个输入不同时，输出为1。使用单个感知机无法直接实现异或运算，因为它不是线性可分的。但可以通过组合多个感知机实现。具体步骤如下：

一种常用的方法是使用两个感知机构建一个多层感知机（Multi-Layer Perceptron，MLP）。MLP由输入层、隐藏层和输出层组成，每个层都由多个感知机（神经元）组成。以下是使用MLP实现异或运算的具体步骤：

构建输入层和隐藏层：

输入层有两个神经元，表示输入的两个二进制位（x1和x2）。
隐藏层有两个神经元，用于引入非线性映射，帮助解决异或运算的非线性可分性。

设置隐藏层的权重和偏置项：

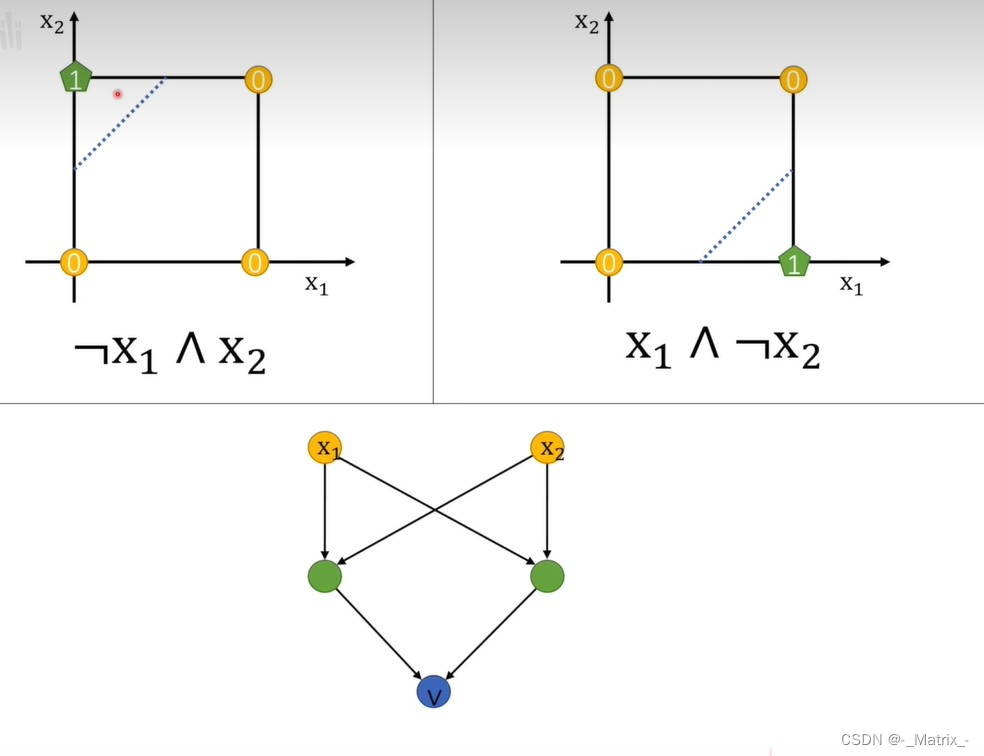
第一个隐藏层神经元，先对x1进行非(NOT)运算，也就是0 为1，非0为0。
然后再进行与(AND)运算。（h1）的权重向量为 w1 = [1, 1]，偏置项为 b1 = -1.5。即：f(x) = sign(x1 + x2 - 1.5)。
第二个隐藏层神经元，先对x2进行非(NOT)运算，也就是0 为1，非0为0。
然后再进行与(AND)运算。（h2）的权重向量为 w2 = [1, 1]，偏置项为 b2 = -1.5。即：f(x) = sign(x1 + x2 - 1.5)。

设置输出层的权重和偏置项：

输出层有一个神经元（y），表示异或运算的结果。
输出层进行或(OR)运算，权重向量为 w3 = [1, 1]，偏置项为 b3 = -0.5。

计算前向传播：

对于输入向量 x = [x1, x2]，首先计算隐藏层神经元的输出：
h1 = sign(w1 * x + b1)
h2 = sign(w2 * x + b2)
然后，将隐藏层神经元的输出作为输入传递给输出层神经元：
y = sign(w3 * [h1, h2] + b3)

输出结果：

当 y = 1 时，表示异或运算的结果为真（1）。
当 y = -1 时，表示异或运算的结果为假（0）。

通过这样的多层感知机结构和非线性激活函数（如符号函数），可以实现异或运算。这个例子中使用了一个隐藏层，但在实际应用中可能需要更多的隐藏层和神经元来处理更复杂的问题。这种多层感知机结构是神经网络的基础，也被称为前馈神经网络（Feedforward Neural Network）。

5. 第二种 异或(XOR)运算：
异或运算是一个二元运算，当两个输入相同时，输出为0；当两个输入不同时，输出为1。使用单个感知机无法直接实现异或运算，因为它不是线性可分的。但可以通过组合多个感知机实现。具体步骤如下：

一种常用的方法是使用两个感知机构建一个多层感知机（Multi-Layer Perceptron，MLP）。MLP由输入层、隐藏层和输出层组成，每个层都由多个感知机（神经元）组成。以下是使用MLP实现异或运算的具体步骤：

1. 构建输入层和隐藏层：
- 输入层有两个神经元，表示输入的两个二进制位（x1和x2）。
- 隐藏层有两个神经元，用于引入非线性映射，帮助解决异或运算的非线性可分性。

2. 设置隐藏层的权重和偏置项：
- 第一个隐藏层神经元（h1）的权重向量为 w1 = [1, 1]，偏置项为 b1 = -0.5。
- 第二个隐藏层神经元（h2）的权重向量为 w2 = [-1, -1]，偏置项为 b2 = 1.5。

3. 设置输出层的权重和偏置项：
- 输出层有一个神经元（y），表示异或运算的结果。
- 输出层的权重向量为 w3 = [1, 1]，偏置项为 b3 = -1.5。

4. 计算前向传播：
- 对于输入向量 x = [x1, x2]，首先计算隐藏层神经元的输出：
  h1 = sign(w1 * x + b1)
  h2 = sign(w2 * x + b2)
- 然后，将隐藏层神经元的输出作为输入传递给输出层神经元：
  y = sign(w3 * [h1, h2] + b3)

5. 输出结果：
- 当 y = 1 时，表示异或运算的结果为真（1）。
- 当 y = -1 时，表示异或运算的结果为假（0）。