难度参考

        难度：困难

        分类：回溯算法

        难度与分类由我所参与的培训课程提供，但需 要注意的是，难度与分类仅供参考。且所在课程未提供测试平台，故实现代码主要为自行测试的那种，以下内容均为个人笔记，旨在督促自己认真学习。

题目

        给定两个整数n 和k，返回1..n中所有可能的k个数的组合。

        示例1:输入:n=4,k= 2

        输出:[[2,4],[3,4],[2,3], [1,2],[1,3],[1,4], ]

        示例2:输入：n=1,k= 1        

        输出：[[1]]

        提示：<=n<=201<=k<=n

思路

        1. 初始化：首先，我们需要一个结果集合来存储所有符合条件的组合，以及一个临时数组（或者称之为路径）来存储当前探索的组合。

        2. 递归与回溯：我们从1开始遍历到n，尝试将每个数加入到当前的组合中，并递归地继续这个过程，直到当前组合的长度等于k，表示我们找到了一个有效的组合，将其添加到结果集中。每次递归调用后，我们需要回溯，即移除当前组合的最后一个元素，以尝试下一个可能的数字。

        3. 终止条件：当当前组合的长度等于k时，将其加入到结果集中，并返回上一层递归。

        具体来说就是，

        1. 定义辅助函数：定义一个辅助函数`combineHelper`，它接受当前数字`start`、当前路径`path`和结果集`result`作为参数。这个函数将负责递归地构建组合。

        2. 递归构建组合：从`start`开始，遍历到n，对于每个数`i`，将其加入到`path`中，然后递归地调用`combineHelper`，将`i+1`作为新的起始点，因为组合是不考虑顺序的，所以我们不需要重复包含之前的数字。

        3. 回溯：在每次递归调用返回后，我们需要从`path`中移除最后加入的数字，这样我们就可以尝试下一个数字。

        4. 收集结果：每当`path`的长度等于k时，就将其复制到结果集中，因为我们找到了一个有效的组合。

示例

        当然，让我们通过一个具体的例子来详细解释这个过程。假设我们有n = 4和k = 2，我们的目标是找到从1到4的所有可能的2个数的组合。

        初始状态

        - 结果集（用于存储所有组合）：[]
        - 当前路径（当前探索的组合）：[]
        - 开始数字：1

        第一层递归

        我们从数字1开始探索。

        - 当前路径：[1]

        接下来，我们进入下一层递归，尝试添加2、3、4到当前路径。

        第二层递归（以1开始）

        - 尝试添加2，当前路径变为[1, 2]。因为当前路径的长度等于k（2），我们找到了一个有效组合，将其添加到结果集中，然后回溯，移除2，当前路径回到[1]。
        - 接着尝试添加3，当前路径变为[1, 3]。同样，这是一个有效组合，添加到结果集，然后回溯，移除3，当前路径再次回到[1]。
        - 最后尝试添加4，当前路径变为[1, 4]。这也是一个有效组合，添加到结果集，然后回溯，移除4，当前路径回到[1]。

        此时，以1开头的所有可能组合都已探索完毕，我们移除1，回到初始状态，当前路径[]，并尝试下一个数字。

        第一层递归（以2开始）

        - 当前路径：[2]

        重复之前的过程：

        - 尝试添加3，当前路径变为[2, 3]。这是一个有效组合，添加到结果集，然后回溯。
        - 尝试添加4，当前路径变为[2, 4]。这也是一个有效组合，添加到结果集，然后回溯。

        此时，以2开头的所有可能组合都已探索完毕，我们继续尝试以3和4开头的组合。

        结果

        按照这个过程，我们最终得到的结果集是：

        - [1, 2]
        - [1, 3]
        - [1, 4]
        - [2, 3]
        - [2, 4]
        - [3, 4]

        这就是所有从1到4中选2个数的组合。

        这个例子展示了回溯算法的工作原理：通过递归探索所有可能的路径，并在满足条件时收集结果，同时使用回溯来撤销最后的选择，从而尝试其他可能的选项。

梳理

        这种方法能够实现的原理基于回溯算法，这是一种通过递归来探索所有可能选择的算法框架，用于解决一类需要遍历所有可能情况来寻找所有解的问题。其核心思想和工作机制可以概括为以下几点：

        1. 选择与探索：从一系列的选项中逐一选择，然后向下探索，直到达到问题的底部（基本情况），这个过程类似于深度优先搜索（DFS）。

        2. 约束条件：在探索过程中，通过约束条件来剪枝，即提前排除那些明显不会得到解的路径。在组合问题中，约束条件可能是组合的长度达到了指定的值。

        3. 回溯：当达到基本情况或者当前路径不满足约束条件时，算法将回溯到上一个决策点，撤销最后的选择，并尝试其他可能的选项。这个过程保证了所有的可能性都被探索过。

        4. 记录解：每当找到一个满足条件的解时，就将其记录下来。在组合问题中，每当构建的组合长度达到指定的k时，就将其添加到结果集中。

        具体到组合问题（如从1到n的所有可能的k个数的组合），回溯算法的工作过程如下：

        - 从1开始，逐一尝试每个数作为组合的第一个数，然后递归地尝试所有可能的下一个数。
        - 在递归过程中，如果当前组合的长度达到了k，就将其记录为一个解。
        - 如果当前组合还没达到k，就继续添加下一个可能的数，直到无法再添加（因为已经达到n或者组合已满）。
        - 每当回溯到某个决策点时，尝试下一个数作为当前位置的数，直到所有数都尝试过。

        通过这种方式，回溯算法能够有效地遍历所有可能的组合，确保找到所有满足条件的解。这种方法之所以有效，是因为它通过递归和回溯机制，实现了对解空间的系统性搜索，同时通过约束条件和撤销选择（回溯）来减少不必要的搜索，从而提高效率。

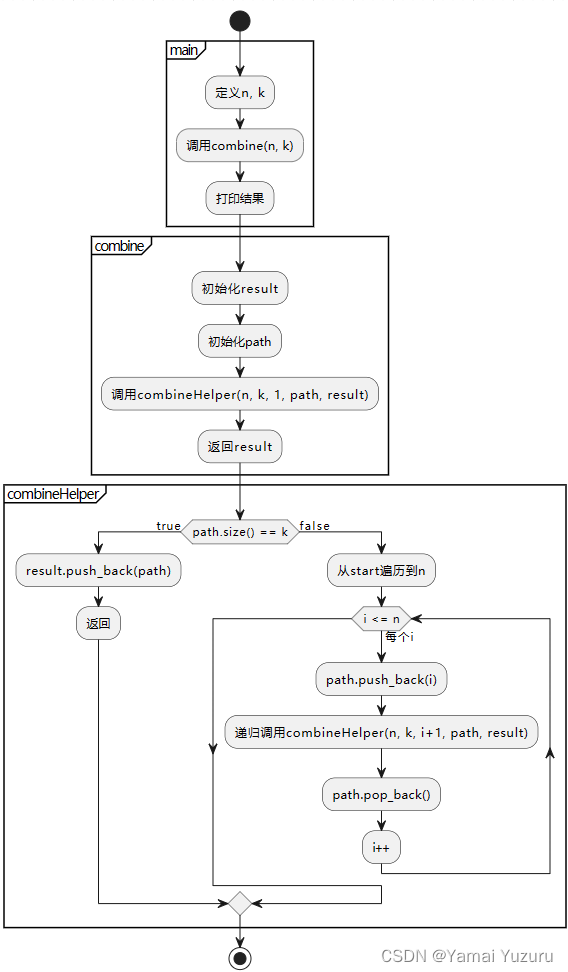
代码

#include <iostream>  // 包含输入输出流库
#include <vector>     // 包含向量库
using namespace std;  // 使用标准命名空间

void combineHelper(int n, int k, int start, vector<int>& path, vector<vector<int>>& result) {
    // 当路径长度等于k时，将其加入结果集
    if (path.size() == k) {
        result.push_back(path);  // 将路径加入结果
        return;
    }
    
    // 从start开始遍历到n
    for (int i = start; i <= n; ++i) {
        // 将当前数字加入路径
        path.push_back(i);
        // 递归调用，注意下一次的起始数字是i+1，因为组合不考虑顺序
        combineHelper(n, k, i + 1, path, result);
        // 回溯，移除路径上的最后一个数字，尝试下一个可能的数字
        path.pop_back();
    }
}

vector<vector<int>> combine(int n, int k) {
    vector<vector<int>> result;  // 存储结果的二维向量
    vector<int> path;  // 存储当前路径的向量
    combineHelper(n, k, 1, path, result);  // 调用辅助函数组合路径
    return result;  // 返回全部结果
}

int main() {
    int n = 4, k = 2;  // 设定初始n和k
    vector<vector<int>> result = combine(n, k);  // 执行组合函数

    cout << "[";  // 输出左括号

    for (int i = 0; i < result.size(); ++i) {  // 遍历结果集
        cout << "[";  // 输出左括号
        for (int j = 0; j < result[i].size(); ++j) {  // 遍历每个组合
            cout << result[i][j];  // 输出当前数字
            if (j < result[i].size() - 1) cout << ",";  // 如果不是该组合的最后一个数字，输出逗号
        }
        cout << "]";  // 输出右括号
        if (i < result.size() - 1) cout << ",";  // 如果不是最后一个组合，输出逗号
    }

    cout << "]" << endl;  // 输出右括号并换行

    // 示例2
    n = 1; k = 1;  // 设定新的n和k
    result = combine(n, k);  // 执行组合函数

    cout << "[";  // 输出左括号

    for (int i = 0; i < result.size(); ++i) {  // 遍历结果集
        cout << "[";  // 输出左括号
        for (int j = 0; j < result[i].size(); ++j) {  // 遍历每个组合
            cout << result[i][j];  // 输出当前数字
            if (j < result[i].size() - 1) cout << ",";  // 如果不是该组合的最后一个数字，输出逗号
        }
        cout << "]";  // 输出右括号
        if (i < result.size() - 1) cout << ",";  // 如果不是最后一个组合，输出逗号
    }

    cout << "]" << endl;  // 输出右括号并换行

    return 0;  // 程序正常结束
}

        时间复杂度：0(n*2^n)

        空间复杂度：0(n)

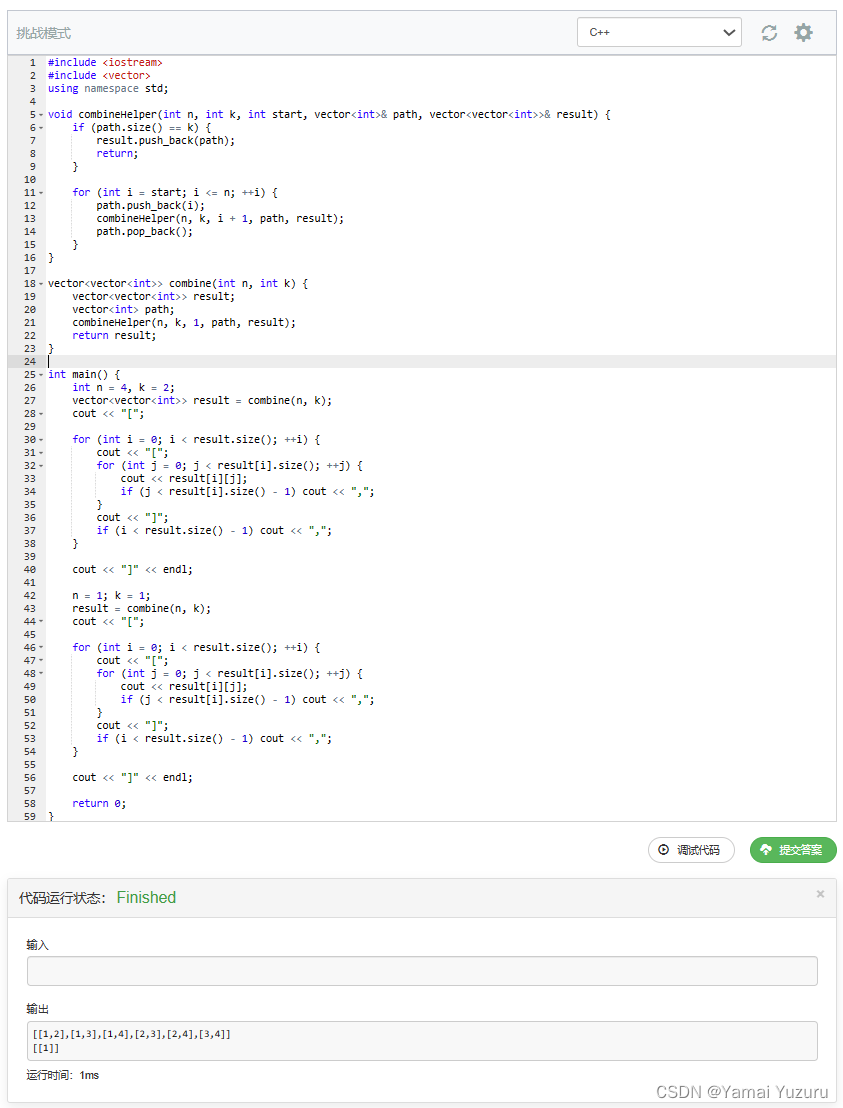
打卡