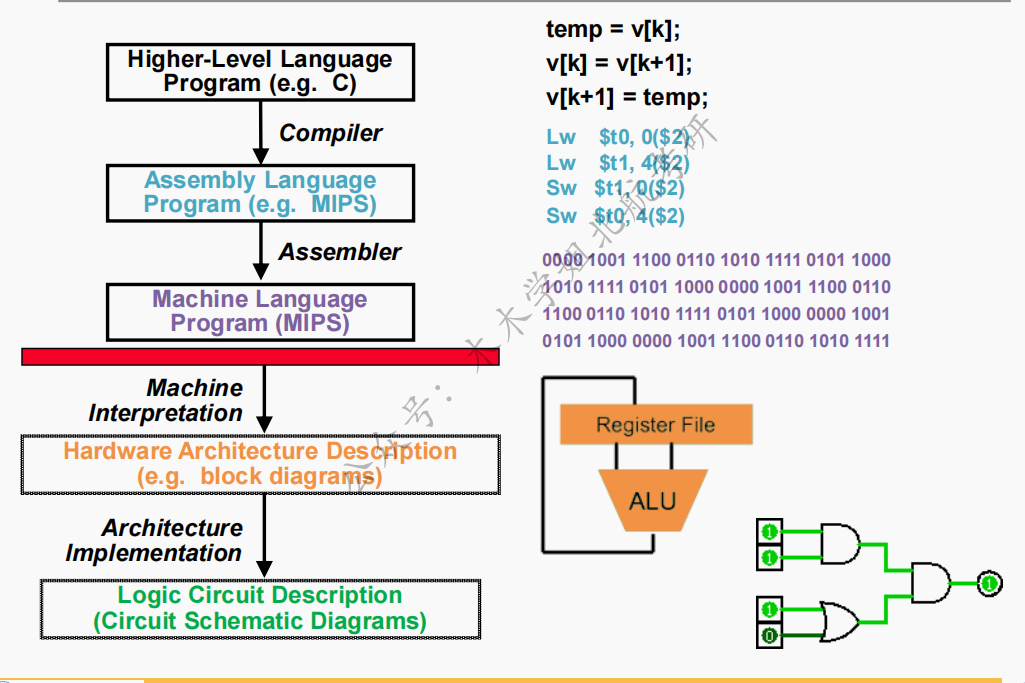
静态函数
背景知识:普通函数都是跨文件可见的,即在文件 a.c 中定义的函数可以在 b.c 中使用。
静态函数:只能在定义的文件内可见的函数,称为静态函数。
语法
staitc void f(void) // 在函数头前面增加关键字 static ,使之成为静态函数
{
// 函数体
}
要点:
- 静态函数主要是为了缩小函数的可见范围,减少与其他文件中重名函数冲突的概率。
- 静态函数一般被定义在头文件中,然后被各个源文件包含。
递归函数
递归概念:如果一个函数内部,包含了对自身的调用,则该函数称为递归函数。
递归问题:
- 阶乘。
- 幂运算。
- 字符串翻转。
要点:
- 只有能被表达为递归的问题,才能用递归函数解决。
- 递归函数必须有一个可直接退出的条件,否则会进入无限递归。
- 递归函数包含两个过程,一个逐渐递进的过程,和一个逐渐回归的过程。
示例:依次输出 n 个自然数。
思路:先输出前面的 n-1 个自然数,再输出最后一个自然数 n 。而要输出前面的 n-1 个自然数,递归调用自身即可。
// 该函数的功能:依次输出 n 个自然数
void f(int n)
{
if(n < 0) // 1,当满足此条件时,不再进行递归。
return;
f(n-1); // 2,递归调用自己,输出前 n-1 个数
printf("%d\n", n); // 3,输出最后一个自然数 n
}
递归调用时,函数的栈内存的变化如下图所示。可见,随着递归函数的层层深入,栈空间逐渐往下增长,如果递归的层次太深,很容易把栈内存耗光。
层层递进时,问题的规模会随之减小,减小到可直接退出的条件时,函数开始层层回归。

递归调用时栈内存的变化
回调函数(钩子函数)
概念:函数实现方不调用该函数,而由函数接口提供方间接调用的函数,称为回调函数。
示例:系统中的信号处理,是一个典型的利用回调函数的情形。

要点:
- 示例中函数 sighandler 是回调函数。
- signal() 将函数回调函数传递给内核,使得内核可以在恰当的时机回调 sighandler。
- 应用开发者和内核开发者只要约定好回调函数的接口,即可各自开发,进度互不影响。