经典格言

不知道正方形对角线与它的边不可通约的人，根本不配人这个称号。——柏拉图（Plato）

好家伙，想象一下柏拉图老兄正站在古希腊的广场上，手里挥舞着一根画着正方形的木棍，满脸认真地对围观的吃瓜群众说：“嘿伙计们，听好了！如果有人连一个正方形的对角线和边长比例是无理数都不知道，那这个人就算不上真正的人类智慧拥有者。换句话说，如果你没搞清楚这个几何小秘密，那你恐怕得去隔壁动物园跟那些只知道用四肢走路不会算数的动物做伴了！”

你看，柏拉图这番话虽然严肃，但如果我们幽默点解读，就像是在说：你可别告诉我你连正方形的对角线长度不能用简单的小数目除以边长就得出结果都不懂，要是这样，你可能得重新考虑下自己是不是属于人类文明圈的一员啦！毕竟，在那个时代，理解和掌握数学真理可是智慧的象征，而正方形对角线的秘密则是入门级别的“智商测试题”呢。

数学习题

一个刘易斯·卡洛尔问题

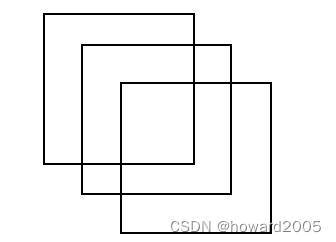
一笔画完这个方形图，既不能穿过任何一条线，也不能把铅笔提起。

古今评注

在数学历史的长河中，巴比伦的智者们犹如古代的面点师傅，他们以卓越的直觉和对几何的深刻理解，将圆周率π捏成了一个香甜可口的数值——$3\frac{1}{8}$，仿佛这是烘焙宇宙真理派中的一个甜蜜近似值。而与此同时，在尼罗河畔智慧璀璨的埃及，那些手握芦苇笔、精研莎草纸的学者们则在《兰德纸草书》（Rhind Papyrus）上揭示了他们的独特配方，用$\frac{256}{81}$这个分数给π做了一次颇为精准的“烹饪”，尽管不如现代蛋糕上的糖霜那么细腻，却也足以让当时的数学家们大快朵颐。

然而，π这道千古难题并没有因为这些早期的大厨们给出了各自的“美食”就轻易被消化掉。它像一个淘气的孩子，藏着不为人知的秘密，拒绝揭开其无理性的面纱，直到将近两千五百年后，德国数学家约翰·兰伯特才扮演了侦探的角色，通过严密的逻辑推理与数学证明，终于锁定了π那不可捉摸的本性：原来π是个顽皮的无理数，它的小数位没有尽头，且无法表示为两个整数的比例。

时光流转至现代社会，这场追寻π奥秘的游戏不仅未因岁月而褪色，反而随着科技厨房里新式“烤箱”——高性能计算机的诞生，以及各种创新“调料”——计算方法的发现，变得愈发热闹非凡。数学家们像是举办一场永不停歇的π数字狂欢节，争相破译隐藏在π那无穷序列背后的神秘图案和音乐旋律，每一串新增的小数位都像是新发现的一颗宇宙星辰，熠熠生辉，令人着迷不已。这场盛宴不仅满足了人们对精确度的渴望，更在娱乐与挑战中彰显了人类对知识边界的不懈探索精神，使得π这位数学世界的超级明星，始终保持着经久不衰的魅力与吸引力。

名人小传 - 柏拉图

柏拉图，这位古希腊哲学界的扛把子、灵魂世界的探索者、理想国的首席设计师，要是搁在今天，那绝对是社交媒体上的大V。他的一生可以用“从数学几何起步，到哲学思想起飞”来形容。

想象一下这个画面：年轻时的柏拉图，可能是个热衷于数独和立体拼图的家伙，整天琢磨着正方形对角线与边长的关系（“喂喂，你们知道吗？这俩家伙根本就不能用简单的小数目整除彼此，不然我可要取消你们做图形的资格了！”），而这一发现也让他认识到真理并非总是直观可见，奠定了他对理念世界追求的基础。

后来，柏拉图拜入苏格拉底门下，开始了他的“哲学修炼之路”。如果苏格拉底是位武林高手，那柏拉图就是他那位勤奋好学的徒弟，每天不是在街市上“拷问”众人的人生智慧，就是在洞穴里冥思苦想——“嘿，伙计们，你们现在看到的世界只是投影，真正的世界就像我们背后的光亮一样，那是纯粹的理念世界哦！”

最后，柏拉图创办了自己的“柏拉图学院”，堪称全球最早的高等学府，口号可能是：“来吧，朋友们，让我们一起跳出‘洞穴’，追求永恒不变的理念真理，顺便再讨论讨论正义城邦怎么建，别忘了带上你们的灵魂和逻辑！”在他的学院里，不仅有严谨的学术探讨，可能还有点类似今天的辩论社团活动，只不过他们辩论的是“什么是美”、“什么是善”这类宇宙终极问题。

总之，柏拉图不仅是位严肃的哲人，也可以被描绘成一个幽默风趣的思想家，用现代的话来说，他大概会是个喜欢用比喻故事来讲大道理，让人笑中带泪地领悟生活与宇宙奥秘的大师级段子手。