上篇文章中，我们学习一个新的模型： 样本对应模型，该模型的套路就是：以结尾位置为出发点，思考两个样本的结尾都会产生哪些可能性 。

而前篇文章中的 纸牌博弈问题 属于 [L , R]上范围尝试模型。该模型给定一个范围，在该范围上进行尝试，套路就是 思考 [L ,R] 两端该如何取舍。

本篇文章我们通过一道中等难度的力扣题，再来熟悉 范围尝试模型 的套路，注意与 上篇文章的最长公共子序列 作对比哦！

力扣516. 最长回文子序列

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例 1：

输入: s = “bbbab”

输出： 4

解释： 一个可能的最长回文子序列为 “bbbb” 。

示例 2:

输入： s = “cbbd”

输出： 2

解释： 一个可能的最长回文子序列为 “bb” 。

学会了 上篇 的 最长公共子序列 之后，这道题目就有一个讨巧的方法：

若翻转输入的字符串，那么原本的字符串与翻转后的字符串的 最长公共子序列 就是 最长回文子序列 。

只需稍加修改，就能套用上面的代码了！

代码

public static int palindromeSubsequence(String s) {
    char[] s1 = s.toCharArray();
    int N = s1.length;
    char[] s2 = new char[N];
    // 翻转 s 字符串
    for (int i = 0; i < N; i++) {
        s2[N - i - 1] = s1[i];
    }
    // 调用 判断最长公共子序列 的动态规划函数
    return longestCommonSubsequence(s1,s2);
}

// 该函数是 上篇文章末尾 的 动态规划版 
public static int longestCommonSubsequence(char[] str1, char[] str2) {
    int N = str1.length;
    int M = str2.length;
    ...
}

除了上面讨巧的办法外，我们依然采用最朴素的 暴力递归 来思考这道题目。

递归的准备

定义递归函数的功能： 返回 str 中 [L ... R] 范围上字符串的最长回文子序列。

思考递归需要的参数： str 字符串，两端范围 L, R。

明确递归的边界条件：

• 当字符串长度为 1 即 L == R 时，找到了一个长度为 1 的回文序列，返回 1 。
• 当字符串长度为 2 即 L == R - 1 时，若两个字符一致，即找到了一个长度为 2 的回文序列，返回 2 。否则返回 1。

思路

这道题就是典型的 范围尝试模型 ，因此，递归就可以按照 开头和结尾两端都会产生哪些可能性 的思路来划分情况：

• 回文子序列 既不以 L 结尾，也不以 R 结尾；
• 回文子序列 以 L 结尾，不以 R 结尾；
• 回文子序列 不以 L 结尾，以 R 结尾；
• 回文子序列 既以 L 结尾，也以 R 结尾。

因为要求 最长 回文子序列，因此要返回这四种情况当中的最大值。

代码

public static int palindromeSubsequence(String s) {
    if (s == null || s.length() == 0) {
        return 0;
    }
    char[] str = s.toCharArray();
    return process(str, 0, str.length - 1);
}

public static int process(char[] str, int L, int R) {
    if (L == R) {
        return 1;
    }
    if (L == R - 1) {
        return str[L] == str[R] ? 2 : 1;
    }
    int p1 = process(str, L + 1, R - 1);
    int p2 = process(str, L, R - 1);
    int p3 = process(str, L + 1, R);
    int p4 = str[L] != str[R] ? 0 : (2 + process(str, L + 1, R - 1));
    return Math.max(Math.max(p1, p2), Math.max(p3, p4));
}

代码解释

注意： 第四种情况 p4 中，如果直接调用 process(str, L, R)，则会产生死循环。为使递归正常运行，要将都以 L 和 R 结尾单独拿出来判断，若相等，去掉两端相等的字符再进行递归调用，回文子序列的长度自然要加上两端 2 的长度。

---

下面我们通过画 dp 表，探寻该递归如何转化为更加优化的动态规划。

以 str = “abcb1a” 为例。

可变的参数有两个，判断长度范围的 L 和 R。因此，需要设置一个二维的 dp 表数组，由于 L, R 的取值范围从 0 开始到字符串长度减一，因此数组大小设置为 dp[N][N] 。

根据递归函数中代码逻辑发现：

1. 当字符串中仅剩一个字符时，回文长度为 1 ，其余均为 0。

    if (L == R) {
        return 1;
    }

因此 dp 数组对角线上的数值均为 1 。

2. 当字符串长度为 2 ，若两个字符一致，即找到了一个长度为 2 的回文序列，返回 2 。否则返回 1。

    if (L == R - 1) {
        return str[L] == str[R] ? 2 : 1;
    }

3. 普遍情况下，依赖 左，下，左下 三个地方的 最大值。

    int p1 = process(str, L + 1, R - 1);
    int p2 = process(str, L, R - 1);
    int p3 = process(str, L + 1, R);
    int p4 = str[L] != str[R] ? 0 : (2 + process(str, L + 1, R - 1));
    return Math.max(Math.max(p1, p2), Math.max(p3, p4));

4. 范围尝试模型的 dp 表最大特点是左下角无效。递归函数调用的是 process(str, 0, str.length - 1)，因此最终答案应该取 dp[0][N-1]== 5。
   

动态规划代码

public static int palindromeSubsequence(String s) {
    if (s == null || s.length() == 0) {
        return 0;
    }
    if (s.length() == 1) {
        return 1;
    }
    char[] str = s.toCharArray();
    int N = str.length;
    int[][] dp = new int[N][N];
    dp[N - 1][N - 1] = 1;
    // 单独填写对角线和相邻斜线的值
    for (int i = 0; i < N - 1; i++) {
        dp[i][i] = 1;
        dp[i][i + 1] = str[i] == str[i + 1] ? 2 : 1;
    }
    // 从下往上 从左往右 找最大值填写
    // 递归中的 p1 情况不需要考虑了
    for (int i = N - 3; i >= 0; i--) {
        for (int j = i + 2; j < N; j++) {
            dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
            if (str[i] == str[j]) {
                dp[i][j] = Math.max(dp[i][j], dp[i + 1][j - 1] + 2);
            }
        }
    }
    return dp[0][N - 1];
}

代码解释

一图胜千言：

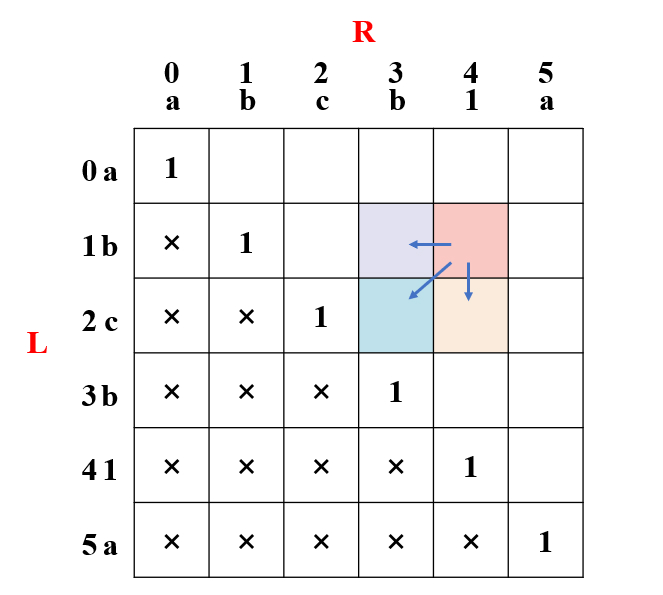
在递归版本中，红色分别依赖紫、蓝、黄，并 取最大值。

    int p1 = process(str, L + 1, R - 1);
    int p2 = process(str, L, R - 1);
    int p3 = process(str, L + 1, R);
    int p4 = str[L] != str[R] ? 0 : (2 + process(str, L + 1, R - 1));
    return Math.max(Math.max(p1, p2), Math.max(p3, p4));

思考一下，紫色部分的值是怎么来的？它也同样依赖了左，下，左下 三个地方的 最大值。因此，紫色 部分一定不小于 蓝色 部分，同理 黄色 部分也一定不小于 蓝色 部分。
因为要求最大值，因此可以忽略掉蓝色部分 p1 的递归调用，只需考虑 p2, p3 的调用。

    dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
    if (str[i] == str[j]) {
        dp[i][j] = Math.max(dp[i][j], dp[i + 1][j - 1] + 2);
    }

因此在动态规划循环中排除了蓝色部分的情况，先求出紫色与黄色的最大值，只有当 str[L] == str[R] 时，再与蓝色部分比出最大值。

这就是使用 严格表依赖 的好处 —— 可以 做进一步的优化！

总结

上篇文章和本文分别讲解了 最长公共子序列问题 和 最长回文子序列问题 。看似很相似的题目，实际使用了两种不同的模型：样本对应模型 和 范围尝试模型 。根据不同模型的套路相信小伙伴也能够轻松应对类似的题目了！

下篇文章我们将介绍一个综合性非常高的题目，并使用一个新的模型来应对，敬请期待吧~

~ 点赞 ~ 关注 ~ 不迷路 ~！！！

------------- 往期回顾 -------------
【算法 - 动态规划】最长公共子序列问题
【算法 - 动态规划】力扣 691. 贴纸拼词
【算法 - 动态规划】原来写出动态规划如此简单！
【算法 - 动态规划】从零开始学动态规划！（总纲）
【堆 - 专题】“加强堆” 解决 TopK 问题！
AC 此题，链表无敌！！！