目录
预备知识:
最小生成树概念:
Kruskal算法:
代码实现如下:
测试:
Prime算法 :
代码实现如下:
测试:
结语:
预备知识:
连通图:在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一 对顶点 都是连通的,则称此图为连通图。
生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
并查集:
由于本文章重点不在讲述并查集,故下面我简单描述并查集的作用,各种方法,源码如下。
并查集的作用:可以将一个数组中的元素分为多个小组的数据结构。
方法:
findRoot(x):查找x的根。
union(int x1, int x2):合并x1和x2。
isSameSet(int x1, int x2):判断两个数字 是不是在同一个集合当中。
import java.util.Arrays;
public class UnionFindSet {
private int[] elem;//底层是数组
public UnionFindSet(int n){
this.elem = new int[n];
Arrays.fill(elem,-1);//整体初始化为-1:代表根
}
/**
* 查找x的根
* @param x
* @return
*/
public int findRoot(int x){
if(x < 0){
throw new IndexOutOfBoundsException("数据不合法");
}
while(elem[x] >= 0){
x = elem[x];
}
return x;
}
/**
* 合并x1和x2
* @param x1
* @param x2
*/
public void union(int x1,int x2){
int index1 = findRoot(x1);
int index2 = findRoot(x2);
if(index1 == index2){//说明x1和x2的根是相同的,不需要进行合并
return;
}
elem[index1] = elem[index1] + elem[index2];
elem[index2] = index1;//将x2合并到x1
}
/**
* 判断两个数字是不是在同一个集合当中
* @param x1
* @param x2
* @return
*/
public boolean isSameSet(int x1,int x2){
int index1 = findRoot(x1);
int index2 = findRoot(x2);
if(index1 == index2){
return true;
}else{
return false;
}
}
}
最小生成树概念:
连通图中的每一棵生成树,都是原图的一个极大无环子图,即:从其中删去任何一条边,生成树 就不在连通;反之,在其中引入任何一条新边,都会形成一条回路。
若连通图由n个顶点组成,则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三 条:
(1) 只能使用图中的边来构造最小生成树。
(2) 只能使用恰好n-1条边来连接图中的n个顶点。
(3) 选用的n-1条边不能构成回路。
构造最小生成树的方法:Kruskal算法和Prim算法。这两个算法都采用了逐步求解的贪心策略。
贪心算法:是指在问题求解时,总是做出当前看起来最好的选择。也就是说贪心算法做出的不是整体最优的选择,而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优解。
Kruskal算法:
Kruskal算法采用全局贪心的策略,其步骤如下:
任给一个有n个顶点的连通网络N={V,E}。
(1)首先构造一个由这n个顶点组成、不含任何边的图G={V,NULL},其中每个顶点自成一个连通分量。
(2)其次不断从E中取出权值最小的一条边(若有多条任取其一),若该边的两个顶点来自不同的连通分量(若相同则不加因为会生成环),则将此边加入到G中。
(3)如此重复,直到所有顶点在同一个连通分量上为止。
核心:每次迭代时,选出一条具有最小权值,且两端点不在同一连通分量上的边,加入生成树。
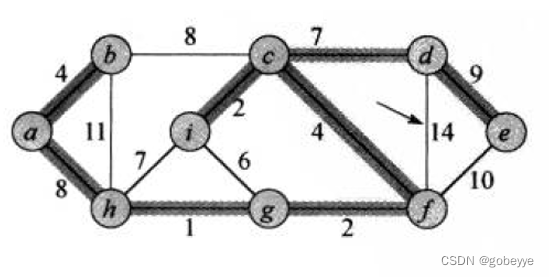
具体过程如下图所示:按照abc..的循序,箭头为当前要操作的位置(不一定能添加,黑色为可添加)。

代码实现如下:
先构造关于Edge的小根堆,由于是自定义类,故要自己实现一个比较器Comparator。
1. 定义优先级队列存储边构建小根堆 跟进权重进行比较。
2. 把矩阵当中的边全部入队列。
3. 定义并查集判断将来两条边是不是在一个集合(避免构成环)。
4. 由于篇幅有限matrix之类的前文实现过这里不在实现有需要的友友可以前往图的概念
static class Edge{
public int srcIndex;
public int destIndex;
public int weight;
public Edge(int srcIndex,int destIndex,int weight){
this.srcIndex = srcIndex;
this.destIndex = destIndex;
this.weight = weight;
}
}
public int kruskal(GraphByMatrix minTree){
//1. 定义优先级队列 存储边 构建小根堆 跟进权重进行比较
PriorityQueue<Edge> minHeap = new PriorityQueue<>(new Comparator<Edge>(){
@Override
public int compare(Edge o1,Edge o2){
return o1.weight - o2.weight;
}
});
int n = matrix.length;
//2. 把矩阵当中的边全部入队列
for(int i = 0;i < n;i++){
for(int j = 0;j < n;j++){
//因为是无向图,所以只入一半就可以 i < j 即可
if(i < j && matrix[i][j] != Integer.MAX_VALUE){
Edge edge = new Edge(i,j,matrix[i][j]);
minHeap.offer(edge);
}
}
}
//3、最后整个的权重
int totalWeight = 0;
int size= 0;
//4.定义并查集 判断将来两条边 是不是在一个集合
UnionFindSet ufs = new UnionFindSet(n);
//5. 出优先级队列的n-1条边
while(size < n-1 &&!minHeap.isEmpty()){
Edge min = minHeap.poll();
int srcIndex = min.srcIndex;
int destIndex = min.destIndex;
//判断是不在在同一个集合当中,在一个集合 就不能添加
if(!ufs.isSameSet(srcIndex,destIndex)){
//打印选出的边
System.out.println("选择的边: "+ arrayV[srcIndex] + "-> "+ arrayV[destIndex] + ":"+
matrix[srcIndex][destIndex]);
?
minTree.addEdgeUseIndex(srcIndex,destIndex,min.weight);
totalWeight += min.weight;
//添加完成之后,说明 可以 合并到同一个集合
ufs.union(srcIndex,destIndex);
size++;
}
}
//如果是 选出n-1条边,否则就说明不是连通图
if(size == n-1){
return totalWeight;
}
//不是连通图, 可能选不出n-1条边 假设一个图中,有其他的顶点独立着
return -1;
}
private void addEdgeUseIndex(int srcIndex,int destIndex,int weight) {
matrix[srcIndex][destIndex] = weight;
//如果是无向图 那么相反的位置 也同样需要置为空
if(!isDirect) {
matrix[destIndex][srcIndex] = weight;
}
}测试:
测试代码对应的图:
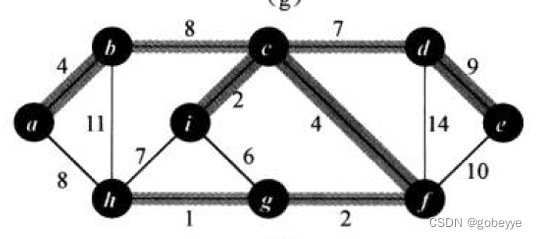
测试代码 :
public static void main(String[] args) {
testGraphMinTreeKruskal();
}
public static void testGraphMinTreeKruskal() {
String str = "abcdefghi";
char[] array =str.toCharArray();
GraphByMatrix g = new GraphByMatrix(str.length(),false);
g.initArrayV(array);
g.addEdge('a', 'b', 4);
g.addEdge('a', 'h', 8);
//g.addEdge('a', 'h', 9);
g.addEdge('b', 'c', 8);
g.addEdge('b', 'h', 11);
g.addEdge('c', 'i', 2);
g.addEdge('c', 'f', 4);
g.addEdge('c', 'd', 7);
g.addEdge('d', 'f', 14);
g.addEdge('d', 'e', 9);
g.addEdge('e', 'f', 10);
g.addEdge('f', 'g', 2);
g.addEdge('g', 'h', 1);
g.addEdge('g', 'i', 6);
g.addEdge('h', 'i', 7);
GraphByMatrix kminTree = new GraphByMatrix(str.length(),false);
System.out.println(g.kruskal(kminTree));
kminTree.printGraph();
}效果:
显然正确💯
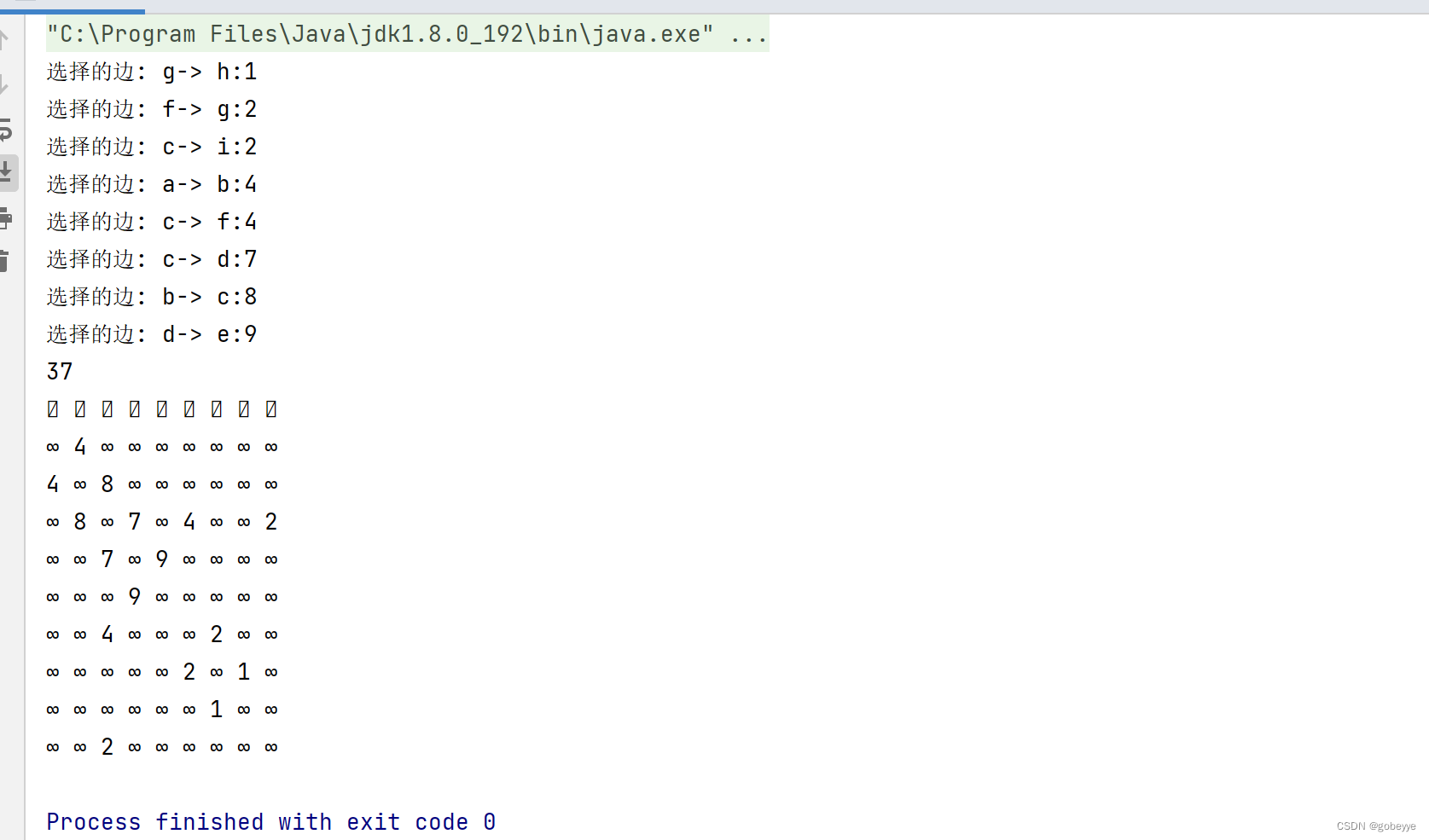
Prime算法 :
Primel算法采用局部贪心的策略,其步骤如下:
按照字母顺序abc....看。

代码实现如下:
由于是局部贪心用两个Set,那么天然就不会有环,故prime可以不用并查集。
1. 先获取当前顶点的下标。
2. 定义一个X集合,把当前的起点下标存进去。
3. 定义一个Y集合,存储目标顶点的元素。
4. 除了刚刚的起点,其他的顶点需要放到Y。
5. 从X集合中的点到Y集合的点中,连接的边中找出最小值放到优先级队列。
6. 把当前顶点连接出去的所有的边放入队列。
7.把这次的目标点,添加到X集合,变成了起点记得把之前的目标点,从Y集合删除掉。
8.遍历刚刚添加的新起点destIndex,连接出去的所有边,再次添加到优先级队列。
public int prim(GraphByMatrix minTree,char chV){
//1. 先获取当前顶点的下标
int srcIndex = getIndexOfV(chV);
int n = arrayV.length;
//2. 定义一个X集合,把当前的起点下标存进去
Set<Integer> setX = new HashSet<>();
//3. 定义一个Y集合,存储目标顶点的元素
Set<Integer> setY = new HashSet<>();
setX.add(srcIndex);
//4. 除了刚刚的起点,其他的顶点需要放到Y集合
for(int i = 0;i < n;i++){
if(i != srcIndex){
setY.add(i);
}
}
//5. 从X集合中的点到Y集合的点中,连接的边中找出最小值放到优先级队列
PriorityQueue<Edge> minHeap = new PriorityQueue<>(new Comparator<Edge>(){
@Override
public int compare(Edge o1,Edge o2){
return o1.weight - o2.weight;
}
});
//6. 把当前顶点连接出去的所有的边放入队列
for(int i = 0;i < n;i++){
if(matrix[srcIndex][i] != Integer.MAX_VALUE){
minHeap.offer(new Edge(srcIndex,i,matrix[srcIndex][i]));
}
}
int size = 0;
int totalWeight = 0;
while(size < n - 1 && !minHeap.isEmpty()){
//7. 取出队列中的第一条边
Edge min = minHeap.poll();
int srcI = min.srcIndex;
int destI = min.destIndex;
//起始点本身就在X集合,所以这里只需要判断目标点即可
if(setX.contains(destI)){
//包含
}else{
//8. 直接将该边 放入最小生成树
minTree.addEdgeUseIndex(srcI,destI,min.weight);
//9. 每选一条边 就打印一条语句
System.out.println("选择的边: "+ arrayV[srcI] + "-> "+ arrayV[destI] + ":"+
matrix[srcI][destI]);
size++;
totalWeight += min.weight;
//10.把这次的目标点,添加到X集合,变成了起点
setX.add(destI);
//11.记得把之前的目标点,从Y集合删除掉
setY.remove(destI);
//12. 遍历刚刚添加的新起点destIndex,连接出去的所有边,再次添加到优先级队列
for(int i = 0;i < n;i++){
// 13. !setX.contains(i) 判断目标点不能再X这个集合 例如: a->b 就包含了b->a
if(matrix[destI][i] != Integer.MAX_VALUE && !setX.contains(i)){
minHeap.offer(new Edge(destI,i,matrix[destI][i]));
}
}
}
}
if(size == n-1){
return totalWeight;
}else{
return -1;
}
}测试:
测试对应的图:
测试代码 :
public static void main(String[] args) {
testGraphMinTreePrime();
}
public static void testGraphMinTreePrime() {
String str = "abcdefghi";
char[] array = str.toCharArray();
GraphByMatrix g = new GraphByMatrix(str.length(), false);
g.initArrayV(array);
g.addEdge('a', 'b', 4);
g.addEdge('a', 'h', 8);
//g.addEdge('a', 'h', 9);
g.addEdge('b', 'c', 8);
g.addEdge('b', 'h', 11);
g.addEdge('c', 'i', 2);
g.addEdge('c', 'f', 4);
g.addEdge('c', 'd', 7);
g.addEdge('d', 'f', 14);
g.addEdge('d', 'e', 9);
g.addEdge('e', 'f', 10);
g.addEdge('f', 'g', 2);
g.addEdge('g', 'h', 1);
g.addEdge('g', 'i', 6);
g.addEdge('h', 'i', 7);
GraphByMatrix primTree = new GraphByMatrix(str.length(), false);
System.out.println(g.prim(primTree, 'a'));
primTree.printGraph();
}效果:
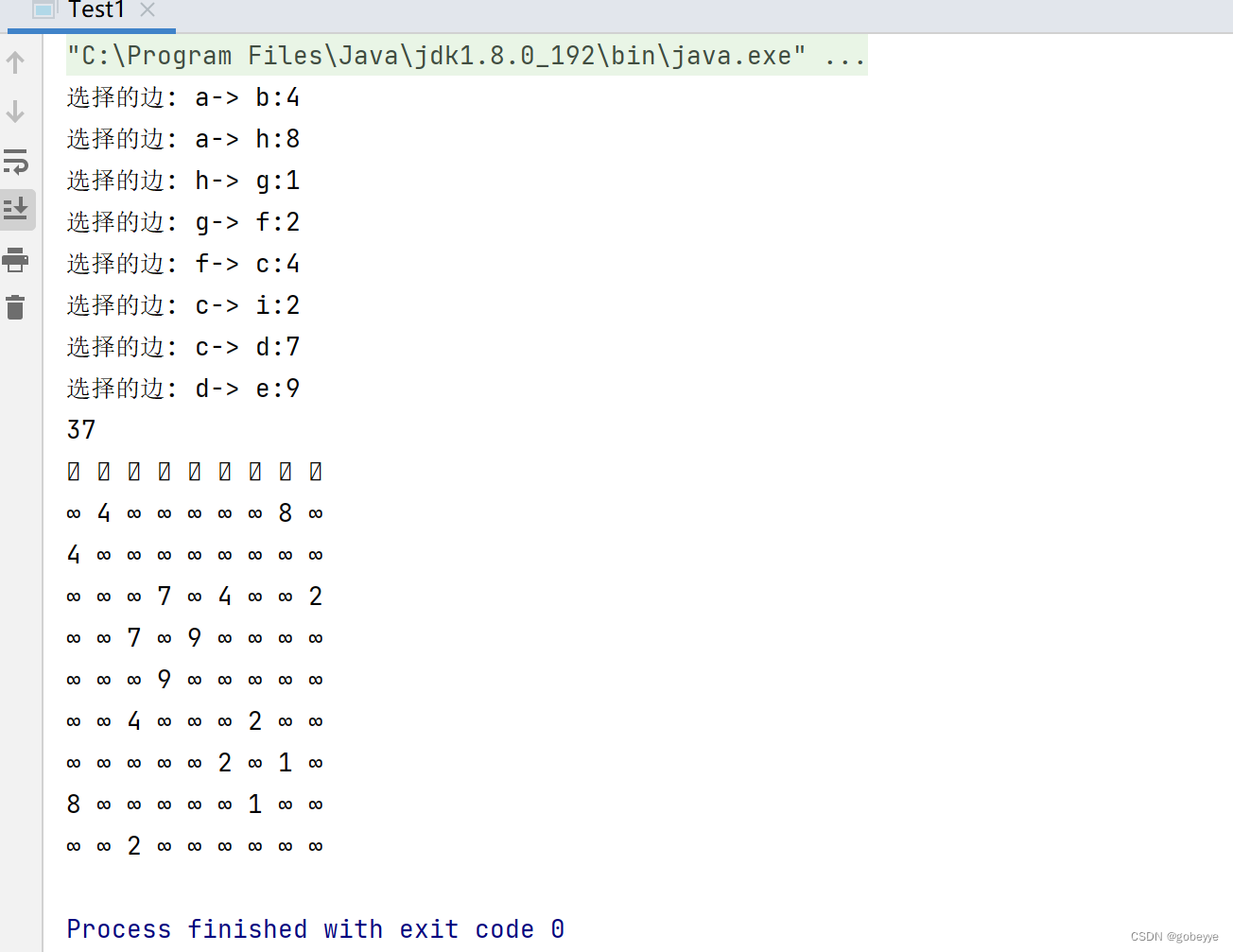
结语:
其实写博客不仅仅是为了教大家,同时这也有利于我巩固自己的知识点,和一个学习的总结,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进,如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注,这可以激励我写出更加优秀的文章。





![[游戏开发][虚幻5]新建项目注意事项](https://img-blog.csdnimg.cn/direct/13ca23567b4844888aa638725ed63840.png)