在简单线性回归或多元线性回归中,我们对误差项做了一些基本假设。
简单线性回归:
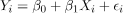
多元线性回归:
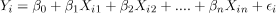
假设条件:
1.误差均值为零
2.误差具有恒定方差
3.误差不相关
4.误差呈正态分布
第2个假设称为同方差性,因此,违反这个假设称为异方差性。
同方差vs异方差

因此,简单地说,我们可以将异方差定义为回归模型中误差项或残差项的方差发生变化的条件。正如你在上图中看到的,在同方差的情况下,数据点是均匀分散的,而在异方差的情况下,数据点不是均匀分散的。
产生异方差的可能原因:
- 通常发生在最大和最小观测值之间有很大范围的数据集中,即当有异常值时。
- 未正确指定模型时。
- 如果观察结果与不同的尺度度量混合。
- 当使用不正确的数据转换来执行回归时。
- 偏度是回归量分布中的一种,也可能是其他一些来源。
异方差的影响:
- 如上所述,线性回归的假设之一(假设2)是不存在异方差。打破这个假设意味着OLS(普通最小二乘)估计量不是最佳线性无偏估计量(BLUE),并且它们的方差不是所有其他无偏估计量中最低的。
- 估计器不再是最佳/有效的。
- 由于估计的回归系数的协方差矩阵的不一致性,假设检验(如t检验、F检验)不再有效。
用残差图识别异方差:
如前文所示,异方差在残差图中产生向外开口的漏斗或向外闭合的漏斗形状。
通过统计检验识别异方差:
异方差的存在也可以使用算法方法进行量化。有一些统计检验或方法可以用来确定异方差的存在或不存在。
- Breusch-Pagan测试:它测试回归误差的方差是否依赖于自变量的值。在这种情况下,存在异方差性。
- White 检验:White 检验确定回归模型中误差的方差是否为常数。为了检验恒定方差,我们进行辅助回归分析:这将来自原始回归模型的平方残差回归到包含原始回归量及其平方和叉积的一组回归量上。
异方差修正:
- 我们可以使用不同规范的模型。
- 加权最小二乘法是常用的统计方法之一。这是普通最小二乘和线性回归的推广,其中允许误差协方差矩阵不同于单位矩阵。
- 使用MINQUE:Minimum Norm Quadratic Unbiased Estimation(MINQUE)的理论包括三个阶段。首先,定义一个一般类的潜在的估计作为二次函数的观测数据,其中的估计涉及到一个向量的模型参数。其次,指定某些约束的估计量的期望属性,如无偏性。第三,选择最佳的估计量通过最小化的“范数”的大小的协方差矩阵的估计。