"Dream it. Wish it. Do it." - Unknown

1. 题目描述

2. 题目分析与解析
2.1 思路一——暴力求解
思路一很简单,就是尝试遍历矩阵的所有元素,如果发现值等于0,就把当前行与当前列的值分别置为0。同时我们需要注意,因为如果出现下图所示的情况:

比如发现matrix[0][0]等于0,我们把第一列和第一行置为0,但是被置为0的行的最后一个元素如上红色框原本也为0,所以这一行与列也要置为0,如果我们单纯把当前行与列覆盖就不知道原来的位置是什么值。并且如果不使用额外空间,我们比如把某一行某一列都置为了0,那么我们在后续遍历时发现这一行这一列的所有元素都为0,都需要处理,那肯定是错误的。所以这就要求我们必须把原始矩阵存储起来。使用额外的O(MN)空间。
2.2 思路二——优化
因为题目中告诉我们仅需要把是matrix中值为0的所在行与所在列元素置为0,那么如果要减少额外的空间使用,我们是不是就可以先遍历matrix单独只存储为0的部分的行列值,然后再将这些为0的值的行列一个个设置为0?这样使用的额外空间就是根据矩阵中为0的元素的个数来计算的。
但是想象一下最坏的情况,如果所有矩阵元素都为0,那么我们是不是就需要M*N个行列,也就是 M*N*2的额外空间大小,那不是还没第一种方法用的额外空间小?
但是如果我们不存储行与列,而是存储当前行与列是否需要置为0的真假,可不可以?如果我们遇到某一个值为0,那么我们就将两个数组的对应第 i 和第二个数组的第 j 个位置置为true,表示我们 i 行,j 列需要置为0,那么即使后续遍历到了其它在当前行或者当前列的某一个值为0的元素,通过查看数组,肯定有一个值为true,只需要把它所单独在的行或者列对应数组的位置置为true就可以。
所以本质上这种方法就是采用两个数组,来表示哪一行需要置为0,哪一列需要置为0。然后再根据数组的真假,将对应行与列置为0。
这种方法会使用O(m + n) 的额外空间。
2.3 思路三——优化2
因为题目提示了
你能想出一个仅使用常量空间的解决方案吗?
那说明肯定有更好的方案,所以我们再想一想。
抓住问题的本质,我们问题的本质不是找哪个元素的值为0,我们的本质是需要将值为0的行于列的元素置为0。并且以前都是空间换时间,现在想要减小空间,那么是不是可以用时间换空间?
根据我的理解,时间与空间实际上就是对于信息的存储形式,而信息总量不变,因此时间增大那么空间就肯定可以变小,时间减小那么额外的信息就需要使用空间来存储。(当然这要建立在完美的算法上,并且也仅仅是个人的理解)
因此我们是不是可以直接不存储那个元素为0,我们只需要一行行遍历矩阵,发现某个元素为0,记录下它所在的列,等到改行遍历完毕,回过头把该行置为0(如果改行有0元素)。在遍历后续行的时候,我们就可以根据前面发现值为0的列将对应位置直接置为0。
代码思路:
-
初始化一个数组,用来记录需要置为0的列
-
遍历矩阵的第一行,发现值为0的元素,就将列值加入数组(如果数组不包含该列的话),然后再将该行所有元素赋值为0
-
如果该行没有值为0的元素,就直接遍历下一行
-
最后遍历column数组,将matrix的第j列的所有元素置为0
这样使用的空间:使用 ArrayList 来存储需要置0的列索引:O(N),在最坏的情况下,如果矩阵的每一列都至少有一个0,则需要存储所有列的索引。
2.4 思路四——优化3
这是我看官方的解析,官方很巧妙的将矩阵的第一行与第一列当作判定数组。其实本质上就和前面的思路2一样,采用两个数组,来表示哪一行需要置为0,哪一列需要置为0,但是这两个数组是用的矩阵原始的第一行与第一列。我将代码加了注释,所以直接读代码应该很清晰:
-
同时需要注意,有些人会问如果第一行或者第一列根本没有0,那你再用它当标志位,之前的值怎么办?
-
所以我需要解释一下:之所以使用第一行与第一列无需再存储它之前的值是因为我们仅仅修改在发现当前行者当前列为0的地方,也就是其它位置我是不动的,如下:
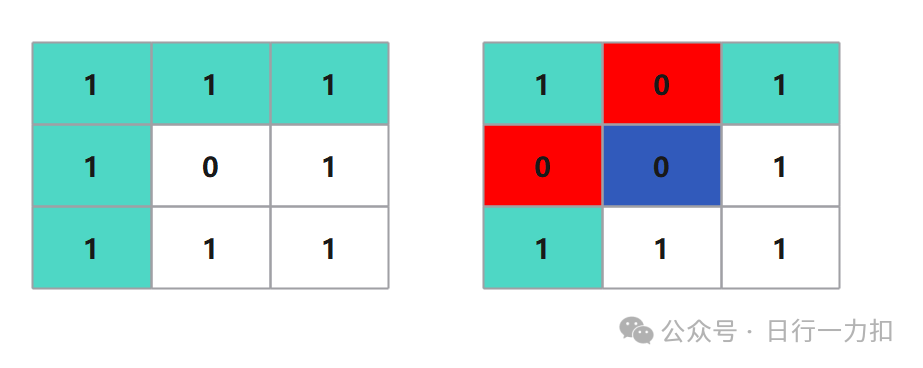
-
当我发现蓝色位置为0,我只更改红色位置的值,这些位置即使第一行与第一列没有0,也是需要更改的。而在结束时如果根据两个判定变量发现第一行与第一列本来没有0,就不需要在做更改了,因为根本没有更改不需要更改的部分。

可以看出这种方法效率还是很高的。
2.5 思路五——优化4
按照上面的官方解析,那就再把思路三种的ArrayList放在矩阵第一行,那也可以使用更少的空间。说做就做,在看了思路三的基础上直接看下面的代码吧


2.6 思路六——优化5——只使用一个变量
在思路五的基础上,我们的判断当前行是否需要置为0的flag是可以省略掉的,如下:
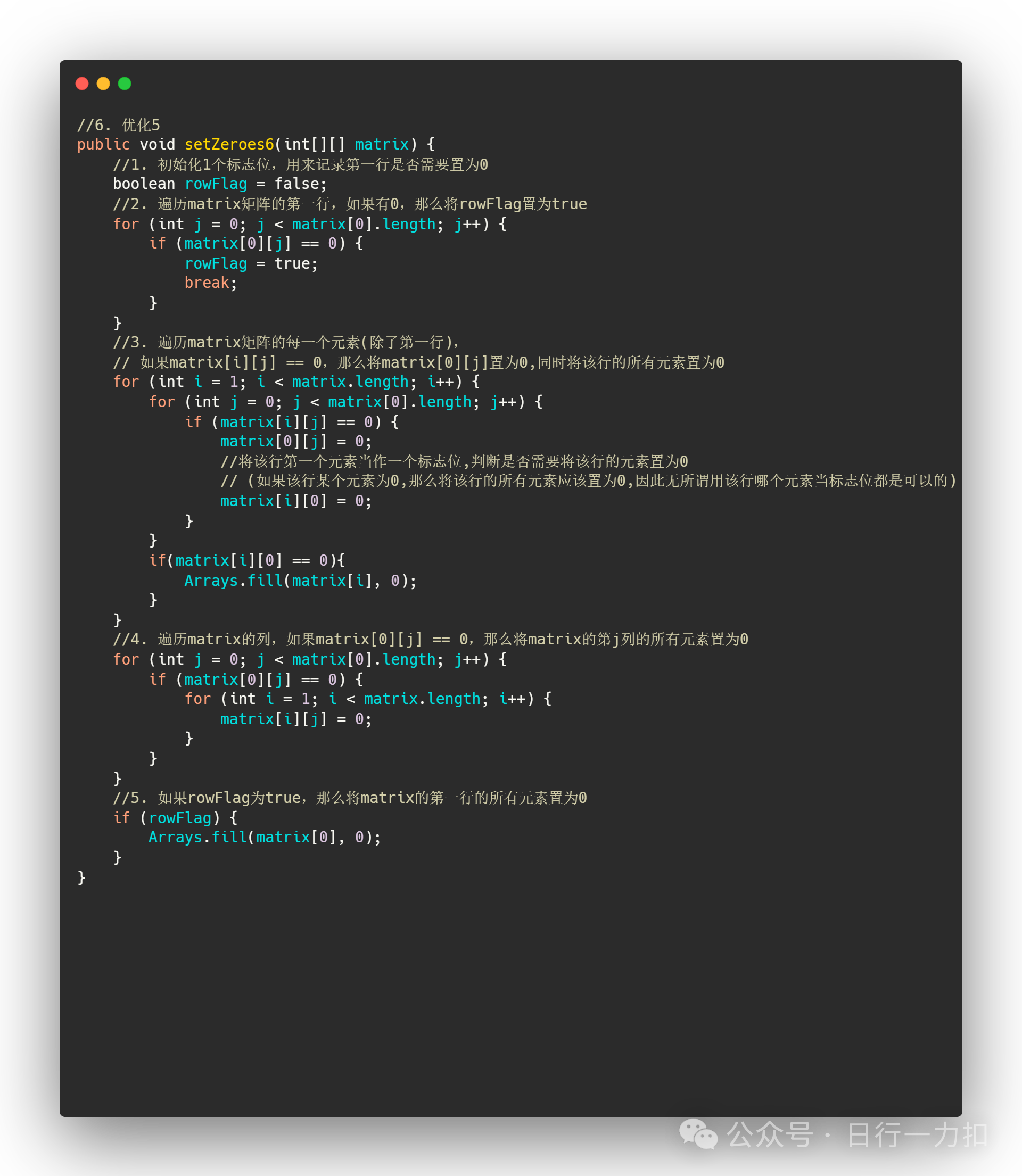
注意这一行:
将该行第一个元素当作一个标志位,判断是否需要将该行的元素置为0
(如果该行某个元素为0,那么将该行的所有元素应该置为0,因此无所谓用该行哪个元素当标志位都是可以的)
按照这种思路只需要使用一个布尔变量就可以完成任务,还是很巧妙的。
3. 代码实现
3.1 思路一

3.2 思路二

3.3 思路三
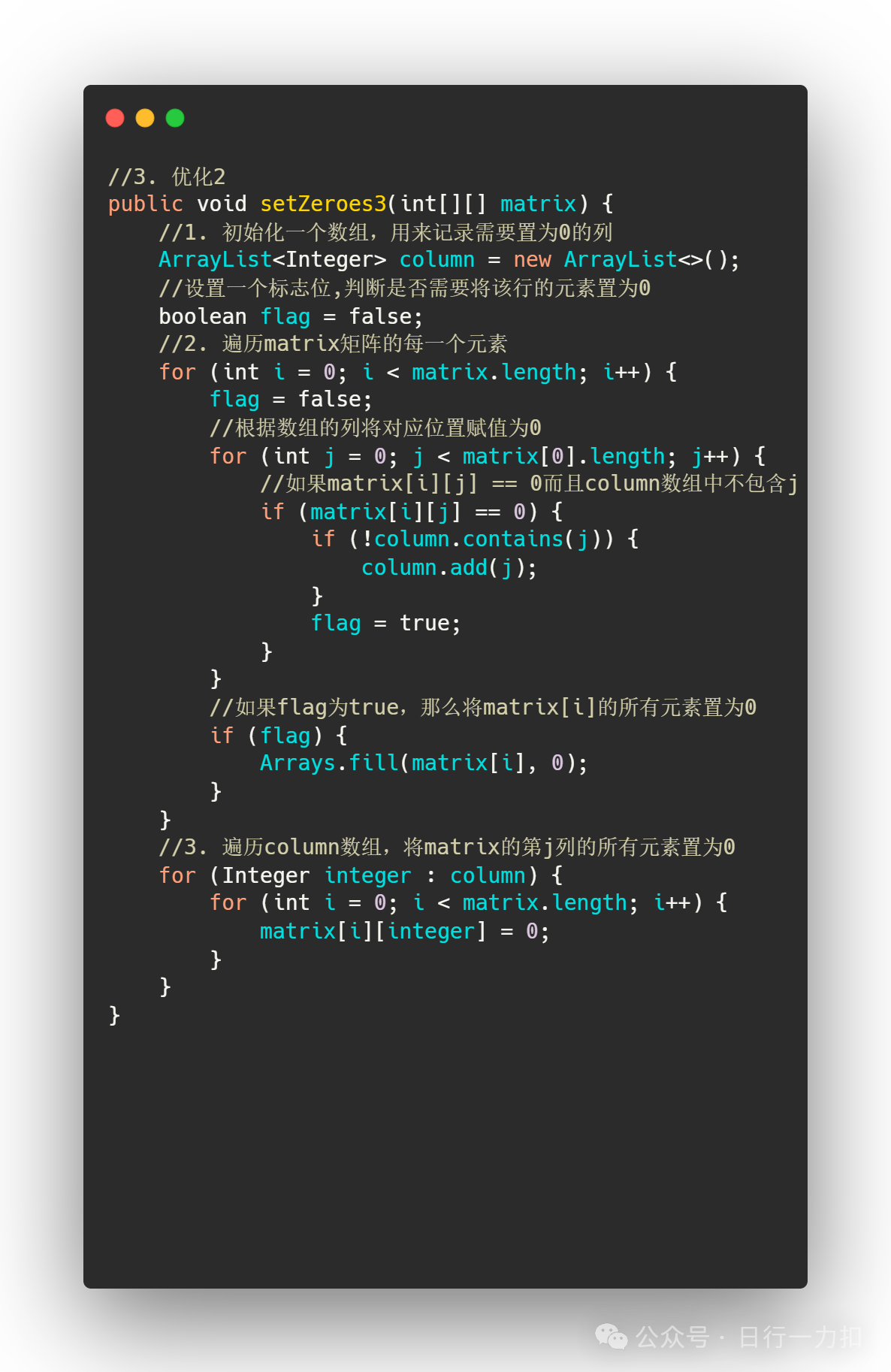
思路四五六见上
4. 相关复杂度分析
1. 暴力求解
-
时间复杂度: (O(M^2N + MN^2))。因为对于矩阵中的每一个元素,都可能需要遍历整行和整列来将它们置为0。
解释:
-
空间复杂度: (O(MN))。需要一个同样大小的矩阵来存储副本。
2. 优化
-
时间复杂度: (O(MN))。首先遍历一遍矩阵来标记需要置0的行和列,然后根据这些标记来置0,每个步骤都是线性的。
-
空间复杂度: (O(M + N))。使用两个额外的数组来记录需要置0的行和列。
3. 优化2
-
时间复杂度: (O(MN^2))。最坏情况下,对于矩阵的每一个元素,都可能需要遍历整个列索引列表来检查是否已经记录了该列。
-
空间复杂度: (O(N))。使用一个ArrayList来记录需要置0的列。
4. 优化3
-
时间复杂度: (O(MN))。遍历整个矩阵两次,一次用于标记,一次用于实际置0操作。
-
空间复杂度: (O(1))。利用矩阵的第一行和第一列来记录0的位置,除了两个额外的标志位以外不需要其他额外空间。
5. 优化4
-
时间复杂度: (O(MN))。虽然有多次遍历,但每次遍历都是线性的,关键操作还是依赖于矩阵的总元素数量。
-
空间复杂度: (O(1))。仅使用一个额外的标志位来记录第一行是否需要置0,直接在原矩阵上操作。
6. 优化5
-
时间复杂度: (O(MN))。和前一种方法类似,遍历矩阵来标记0的位置,然后根据这些标记来置0。
-
空间复杂度: (O(1))。使用矩阵的第一行和第一个元素来记录行和列是否需要置0,没有使用其他额外空间。
但显然,随着优化的进行,我们尽量减少了空间复杂度,直至达到常数空间复杂度的解法,同时保持了时间复杂度为线性。总之来说还是很有意思的。