目录

图的遍历概念：

图的广度优先遍历（BFS）：

代码实现如下：

测试如下：

注意：

图的深度优先遍历（DFS）：

代码实现如下：

测试如下：

总代码：

结语：

---

图的遍历概念：

给定一个图G和其中任意一个顶点v0，从v0出发，沿着图中各边访问图中的所有顶点，且每个顶点仅被遍历一次。"遍历"即对结点进行某种操作的意思。由于考试大多考邻接矩阵(GraphByMatrix)，故下面的遍历都是用邻接矩阵(GraphByMatrix)，不是邻接表(GraphByNode)。

图的广度优先遍历（BFS）：

广度优先遍历类似于我们前面所学二叉树的层序遍历，一层一层的走，故可以使用队列来模拟实现。

比如：现在有三个抽屉（每个抽屉包含一个红色盒子，红色盒子中又包含一个绿色盒子），所需东西在那个抽屉不清楚，现在要将其找到，广度优先遍历的做法是：

（1）先将三个抽屉打开，在最外层找一遍。

（2）将每个抽屉中红色的盒子打开，再找一遍。

（3）最后将红色盒子中绿色盒子打开，再找一遍。

直到找完所有的盒子，注意：每个盒子只能找一次，不能重复找。

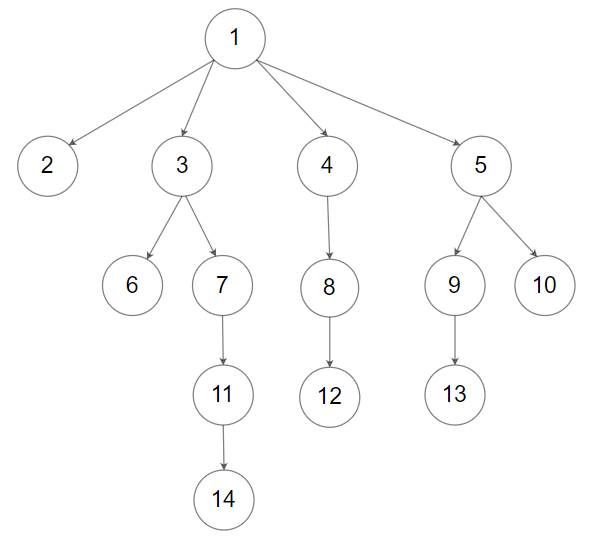
例如下图：

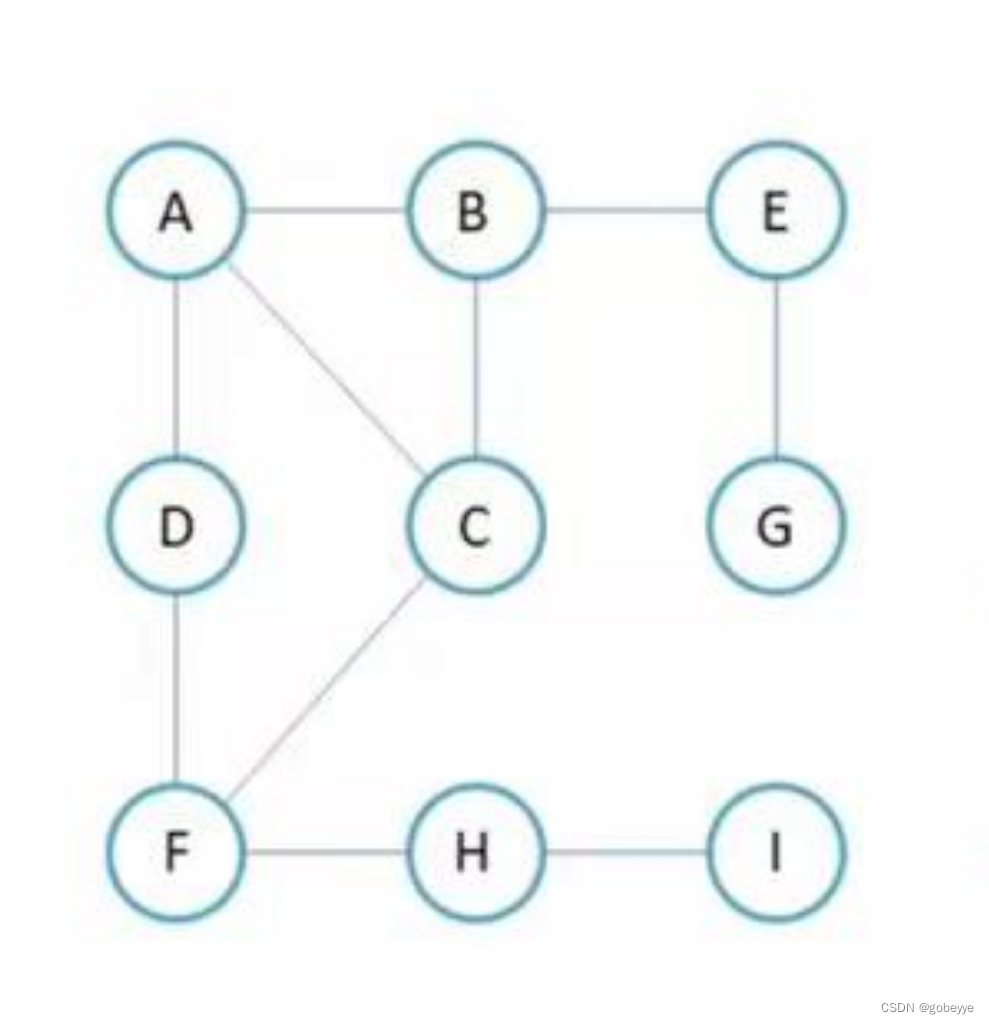
该图的广度优先遍历过程如下：

故其广度优先遍历的结果为：ABCDEFGHI。

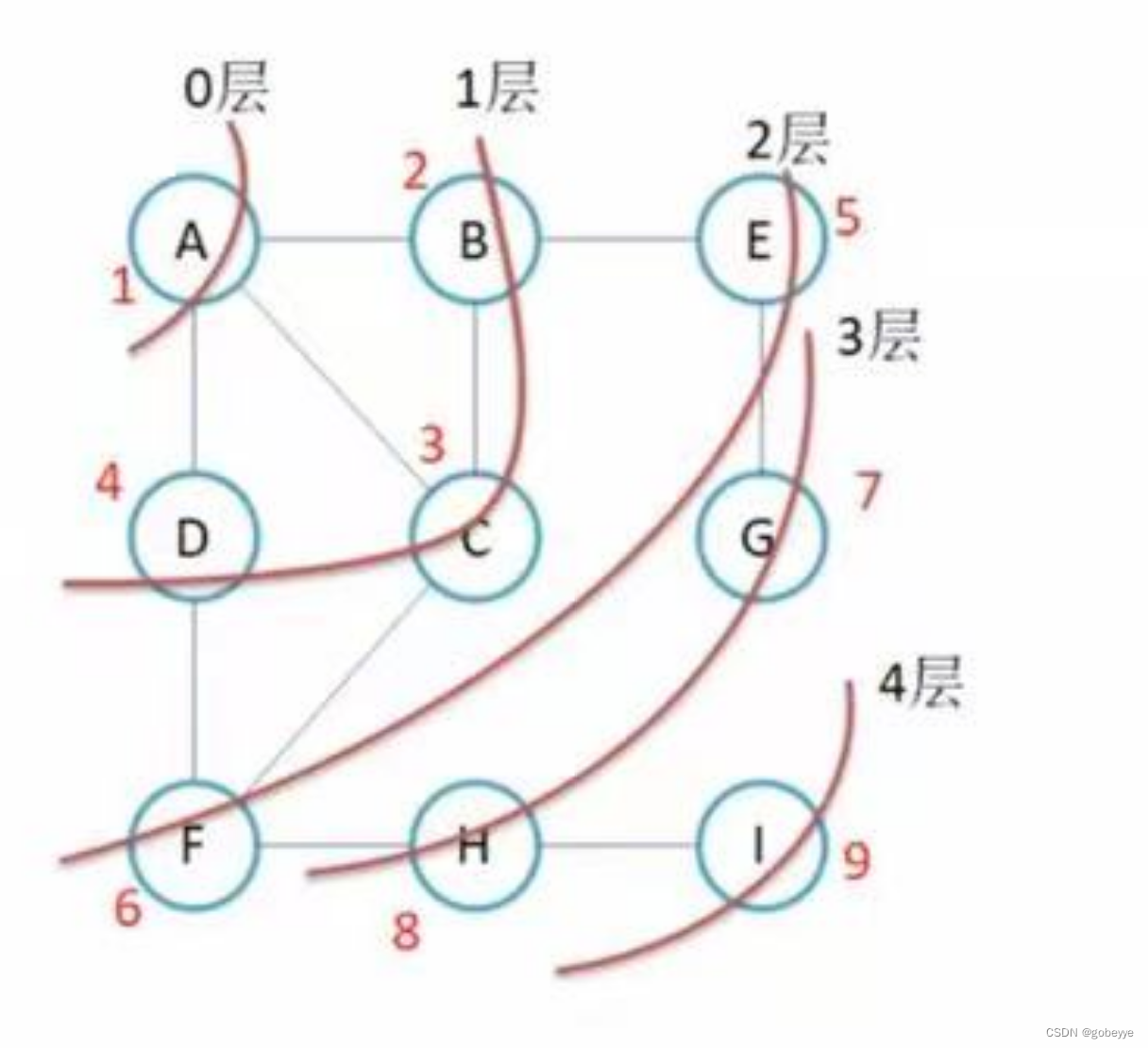
代码实现如下：

1、初始化一个布尔类型数组visited，默认所有顶点都没有被遍历到。

2、获取当前开始的顶点V 的下标。

3、定义一个队列，存储当前需要遍历的顶点的下标。

4、取出当前队列的头部。

5、把当前的顶点的这一行都放到队列。

由于getIndexOfV，arrayV，matrix在上一篇文章中已经非常详细的描述过，故这里我只解释其作用，如若需要源码和更加详细的解释请友友前往：图的存储结构 

（1）geiIndexOfV 获取顶点元素在其数组中的下标 。

（2）arrayV 顶点元素的一维数组。

（3）matrix 利用matrix二维数组来存储顶点之间边的权重。

/**
     * 广度优先遍历
     * @param v
     */
    public void bfs(char v){
        //1、初始化一个布尔类型数组，默认所有顶点都没有被遍历到
        boolean[] visited = new boolean[arrayV.length];
        //2、获取当前开始的顶点V的下标
        int index = getIndexOfV(v);
        //3、定义一个队列，存储当前需要遍历的顶点的下标
        Queue<Integer> qu = new LinkedList<>();
        qu.offer(index);//起点放进来
        while(!qu.isEmpty()){
            //4、取出当前队列的头部
            int top = qu.poll();
            System.out.print(arrayV[top]+":"+"-> ");
            visited[top] = true;
            //5、把当前的顶点的这一行都放到队列
            for(int i = 0;i < arrayV.length;i++){
                //如果这一行的i下标不等于MAX_VALUE，并且也没有被访问过
                if(matrix[top][i] != Integer.MAX_VALUE && visited[i] == false){
                    qu.offer(i);
                    //注意，防止重复打印
                    visited[i] = true;
                }
            }
        }
        System.out.println("null");
    }

测试如下：

测试代码均围绕下图进行：

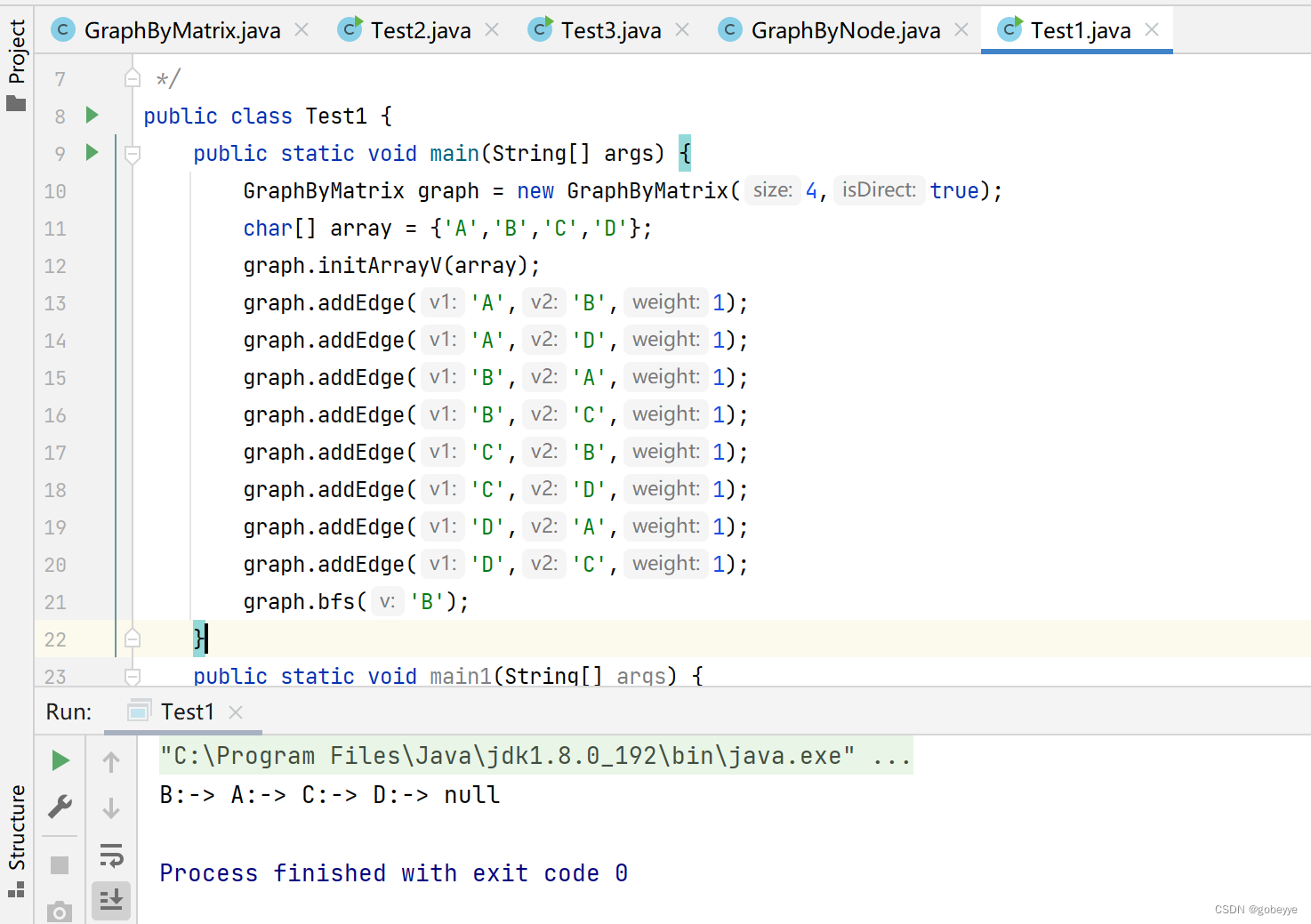
遍历结果为BACD显然符合我们的预期。 

注意：

下面话红线的地方不能省去。

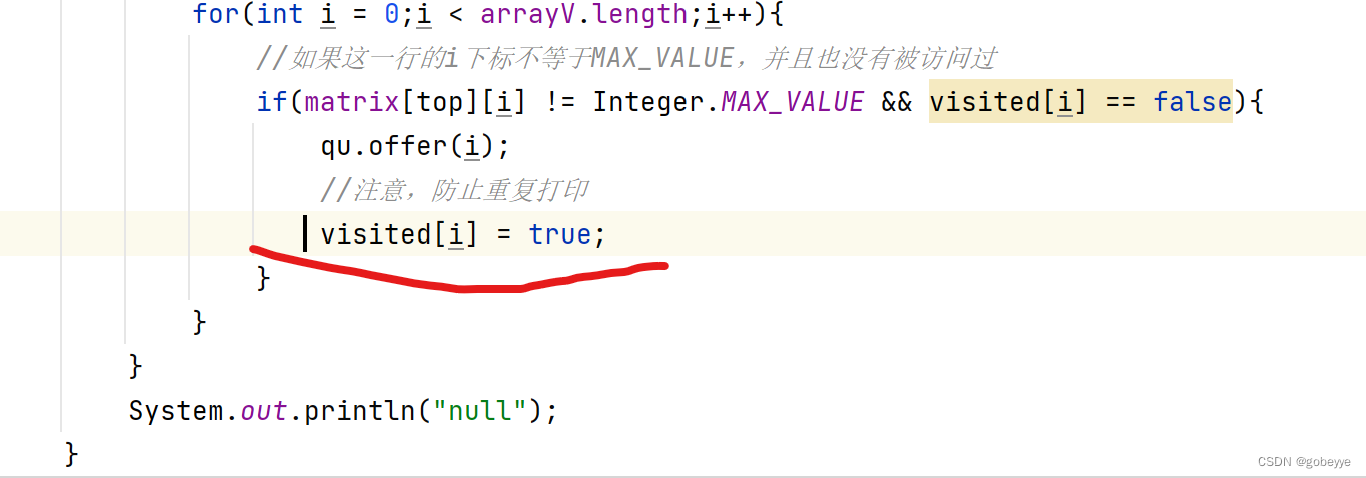
如若省去会发生重复遍历例如：

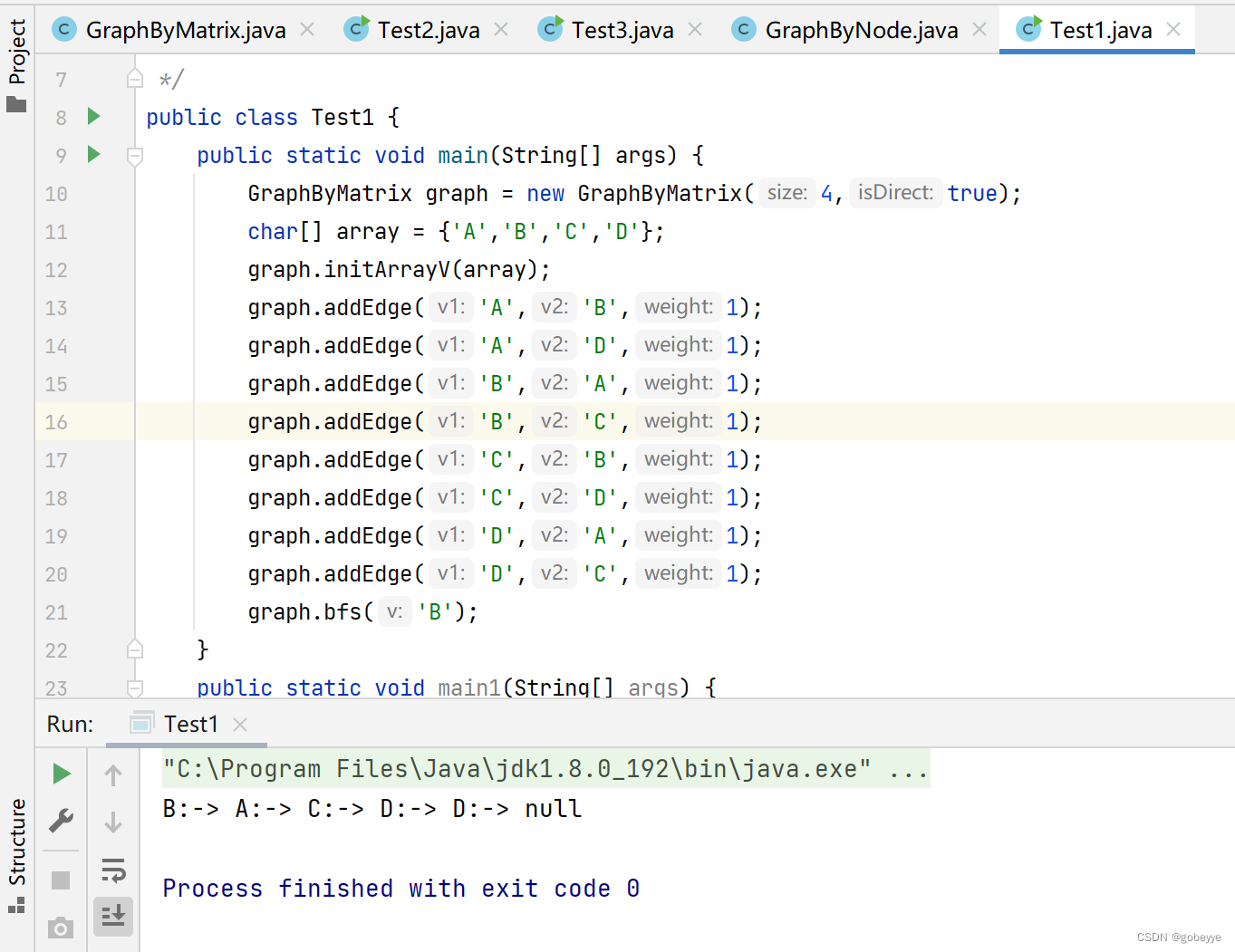发生了DD的重复打印。

那为什么会发生重复打印呢？这是因为在C出队时，D已经在队列中了但是其还是false，故C出队会再次把D入队，这样就会重复打印。具体过程如下动图：

解决方法：在入队时一起把元素对应下标的visited数组设置为false。

为了方便友友调试下面将测试代码给出：

public static void main(String[] args) {
        GraphByMatrix graph = new GraphByMatrix(4,true);
        char[] array = {'A','B','C','D'};
        graph.initArrayV(array);
        graph.addEdge('A','B',1);
        graph.addEdge('A','D',1);
        graph.addEdge('B','A',1);
        graph.addEdge('B','C',1);
        graph.addEdge('C','B',1);
        graph.addEdge('C','D',1);
        graph.addEdge('D','A',1);
        graph.addEdge('D','C',1);
        graph.bfs('B');
    }

图的深度优先遍历（DFS）：

图的深度优先遍历类似于前面所学二叉树的前序遍历，有路就走，走完没路了再回退，使用递归来实现。

比如：现在有三个抽屉（每个抽屉包含一个红色盒子，红色盒子中又包含一个绿色盒子），所需东西在那个抽屉不清楚，现在要将其找到，深度优先遍历的做法是：

（1）先将第一个抽屉打开，在最外层找一遍。

（2）将第一个抽屉中红色的盒子打开，在红色箱子里找一遍。

（3）将红色盒子中绿色盒子打开，在绿箱子里找一遍。

（4）递归查找剩余两个箱子。

深度优先遍历：将一个抽屉一次性遍历完（包括该抽屉中包含的小盒子），再去递归遍历其它盒子。

其过程如图所示：

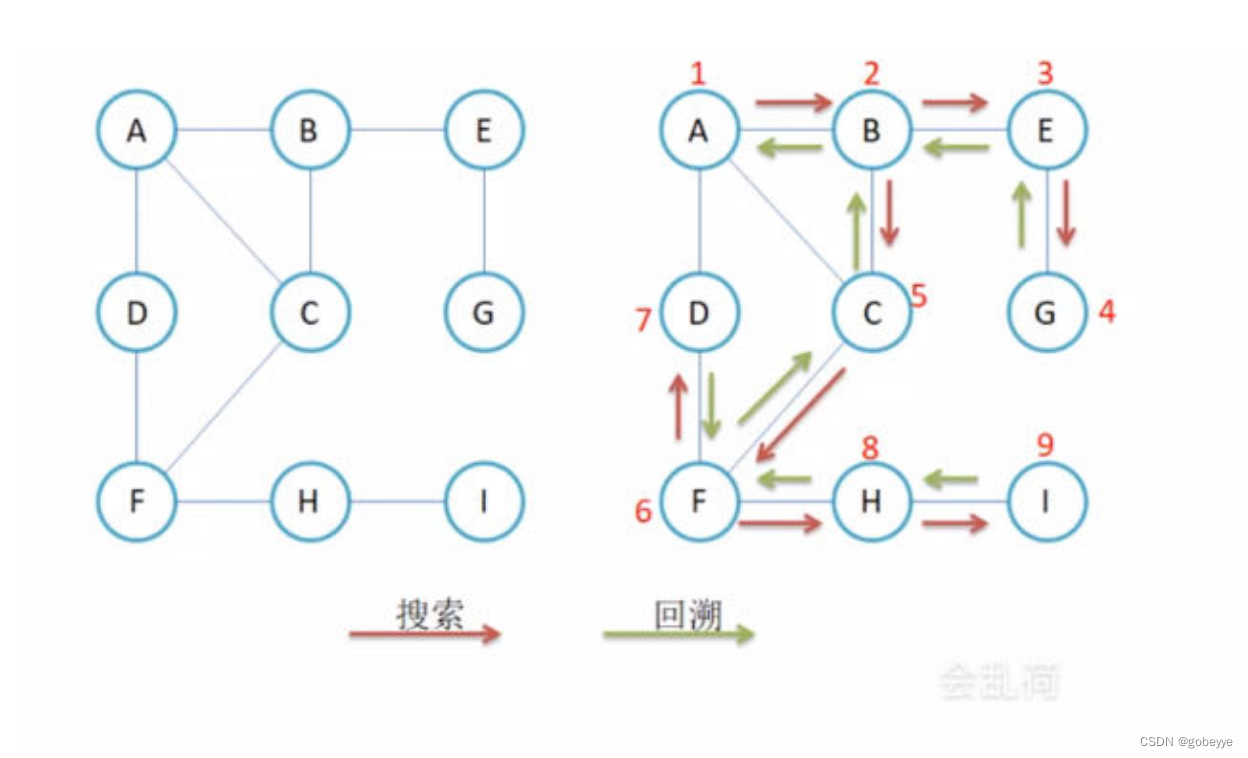
其深度优先遍历结果为：ABEGCFDHI。

代码实现如下：

实现一个方法dfschild来进行递归，为什么不用dfs直接递归呢？这是因为如果直接把dfs递归哪visited会一直被开辟，堆上的内存占用太大，要把visited设置在dfs外面才行。

部分流程和前面所说的广度优先遍历类似，关于getIndexOfV，arrayV，matrix在广度优先遍历那已解释故这里不再过多描述。

 /**
     * 给定顶点，从顶点处开始进行深度优先遍历
     * @param v
     */
    public void dfs(char v){
        //1、初始化一个布尔类型数组，默认所有顶点都没有被遍历到
        boolean[] visited = new boolean[arrayV.length];
        //2、获取当前开始的顶点V 的下标
        int index = getIndexOfV(v);
        //3、开始从index位置进行深度遍历
        dfsChild(index,visited);
        System.out.print("null");
    }
    /**
     * 从index位置开始深度优先遍历
     * @param index
     * @param visited
     */
    private void dfsChild(int index,boolean[] visited){
        System.out.print(arrayV[index]+":"+"-> ");
        visited[index] = true;
        //当前index位置的，所有的连接点都在这一行
        for(int i = 0;i < arrayV.length;i++){
            //如果这一行的i下标不等于0，并且也没有被访问过
            if(matrix[index][i] != Integer.MAX_VALUE && visited[i] == false){
                dfsChild(i,visited);
            }
        }
    }

测试如下：

遍历结果为：BADC显然符合我们的预期。

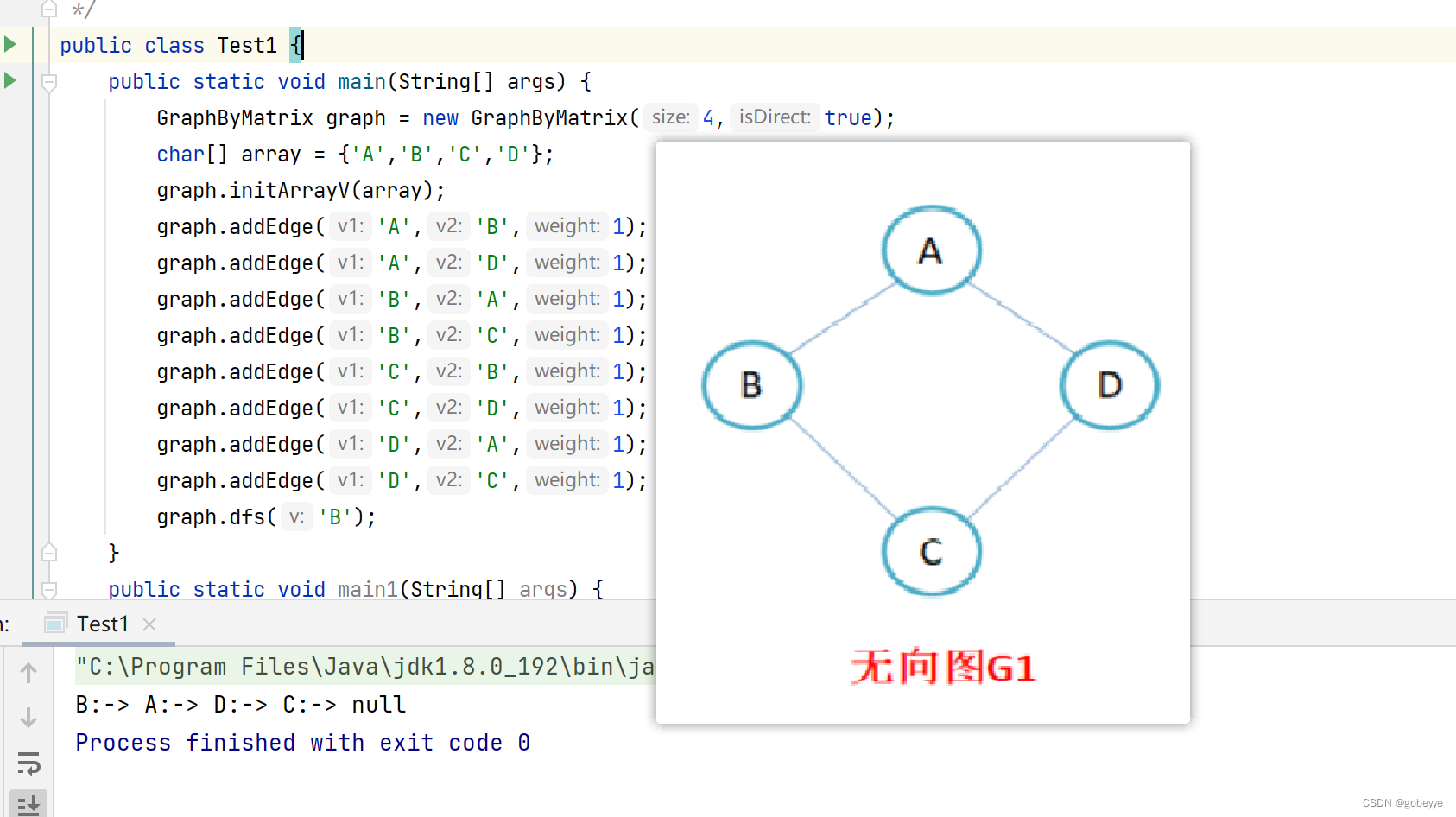
总代码：

import java.sql.SQLOutput;
import java.util.Arrays;
import java.util.Queue;
import java.util.LinkedList;
public class GraphByMatrix {
    private char[] arrayV;//存放顶点·
    private int[][] matrix;//存放边
    private boolean isDirect;//是否是有向图
    public GraphByMatrix(int size,boolean isDirect){
        arrayV = new char[size];
        matrix = new int[size][size];
        for(int i = 0;i < size;i++){
            Arrays.fill(matrix[i],Integer.MAX_VALUE);
        }
        this.isDirect = isDirect;
    }
    /**
     * 初始化
     * @param array 顶点集合
     */
    public void initArrayV(char[] array){
        for(int i = 0;i < array.length;i++){
            arrayV[i] = array[i];
        }
    }

    /**
     *
     * @param v1 起始
     * @param v2 终点
     * @param weight 权值
     */
    public void addEdge(char v1,char v2,int weight){
        int index1 = getIndexOfV(v1);
        int index2 = getIndexOfV(v2);
        matrix[index1][index2] = weight;
        if(!isDirect){
            matrix[index2][index1] = weight;
        }
    }

    /**
     * 获取顶点元素在其数组中的下标
     * @param v
     * @return
     */
    public int getIndexOfV(char v){
        for(int i = 0;i < arrayV.length;i++){
            if(v == arrayV[i]){
                return i;
            }
        }
        return -1;
    }

    /**
     * 获取顶点的度
     * @param v
     * @return
     */
    public int getDevOfV(char v){
        int indexV = getIndexOfV(v);
        int count = 0;
        for(int i = 0;i < arrayV.length;i++){
            if(matrix[indexV][i] != Integer.MAX_VALUE){
                count++;
            }
        }
        if(isDirect){
            for(int i = 0;i < arrayV.length;i++){
                if(matrix[i][indexV] != Integer.MAX_VALUE){
                    count++;
                }
            }
        }
        return count;
    }
    public void printGraph(){
        for(int i = 0;i < arrayV.length;i++){
            System.out.print(arrayV[i] + " ");
        }
        System.out.println();
        for(int i = 0;i < matrix.length;i++){
            for(int j = 0;j < matrix[i].length;j++){
                if(matrix[i][j] == Integer.MAX_VALUE) {
                    System.out.print("∞ ");
                }else {
                    System.out.print(matrix[i][j]+" ");
                }
            }
            System.out.println();
        }
    }
    //广度优先遍历

    /**
     * 广度优先遍历
     * @param v
     */
    public void bfs(char v){
        //1、初始化一个布尔类型数组，默认所有顶点都没有被遍历到
        boolean[] visited = new boolean[arrayV.length];
        //2、获取当前开始的顶点V的下标
        int index = getIndexOfV(v);
        //3、定义一个队列，存储当前需要遍历的顶点的下标
        Queue<Integer> qu = new LinkedList<>();
        qu.offer(index);//起点放进来
        while(!qu.isEmpty()){
            //4、取出当前队列的头部
            int top = qu.poll();
            System.out.print(arrayV[top]+":"+"-> ");
            visited[top] = true;
            //5、把当前的顶点的这一行都放到队列
            for(int i = 0;i < arrayV.length;i++){
                //如果这一行的i下标不等于MAX_VALUE，并且也没有被访问过
                if(matrix[top][i] != Integer.MAX_VALUE && visited[i] == false){
                    qu.offer(i);
                    //注意，防止重复打印
//                    visited[i] = true;
                }
            }
        }
        System.out.println("null");
    }
    //图的深度优先遍历

    /**
     * 给定顶点，从顶点处开始进行深度优先遍历
     * @param v
     */
    public void dfs(char v){
        //1、初始化一个布尔类型数组，默认所有顶点都没有被遍历到
        boolean[] visited = new boolean[arrayV.length];
        //2、获取当前开始的顶点V 的下标
        int index = getIndexOfV(v);
        //3、开始从index位置进行深度遍历
        dfsChild(index,visited);
        System.out.print("null");
    }
    /**
     * 从index位置开始深度优先遍历
     * @param index
     * @param visited
     */
    private void dfsChild(int index,boolean[] visited){
        System.out.print(arrayV[index]+":"+"-> ");
        visited[index] = true;
        //当前index位置的，所有的连接点都在这一行
        for(int i = 0;i < arrayV.length;i++){
            //如果这一行的i下标不等于0，并且也没有被访问过
            if(matrix[index][i] != Integer.MAX_VALUE && visited[i] == false){
                dfsChild(i,visited);
            }
        }
    }
}

结语：

其实写博客不仅仅是为了教大家，同时这也有利于我巩固自己的知识点，和一个学习的总结，由于作者水平有限，对文章有任何问题的还请指出，接受大家的批评，让我改进，如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注，这可以激励我写出更加优秀的文章。