常规的语义相关性评价可以从检索、排序两个方面进行。这里只贴代码。详细可见知乎https://zhuanlan.zhihu.com/p/682853171

检索

精确率

def pre(true_labels=[],pre_labels=[]):
    """
    :param true_labels: 正样本索引
    :param pre_labels: 召回样本索引
    :return: 精确率
    """
    Predict_Pos = len(pre_labels)
    TP = len( set(true_labels) & set(pre_labels) )
    return TP / Predict_Pos 

计算示例：略。

召回率

def rec(true_labels=[],pre_labels=[]):
    """
    :param true_labels: 正样本索引
    :param pre_labels: 召回样本索引
    :return: 召回率
    """
    TP = len( set(true_labels) & set(pre_labels) )
    All_Pos = len(true_labels)
    return TP / All_Pos

计算示例：略。

ROC曲线和AUC

def roc_curve(rec_list=[], pre_list=[]):
    """
    :param rec_list: 召回率列表
    :param pre_list: 精确率列表
    :return: AUC
    """
    assert len(rec_list) == len(pre_list)
    # 召回、准确临界情况
    rec_list += [1, 0]
    pre_list += [0, 1]
    # 同一条横/纵轴有多个点的情况: 相同recall值下取precision的均值。
    rec_dict = {} # recall:[多个precisions]
    for i in range(len(rec_list)):
        if rec_list[i] not in rec_dict:
            rec_dict[rec_list[i]] = [pre_list[i]]
        else:
            rec_dict[rec_list[i]].append(pre_list[i])
    rec_list = []
    pre_list = []
    for key in rec_dict:
        rec_list.append(key)
        pre_list.append(sum(rec_dict[key])/len(rec_dict[key]))
    # 重排序
    rec_list_sorted = sorted(rec_list)
    pre_list_sorted = [pre_list[idx] for idx, _ in sorted(enumerate(rec_list), key=lambda x: x[1])]
    print(f"recall:{rec_list_sorted}. precision:{pre_list_sorted}.")
    # ROC曲线
    plt.plot(rec_list_sorted, pre_list_sorted)  # 画折线图
    plt.xlabel("Recalls")
    plt.ylabel("Precisions")
    plt.show()  # 显示图形
    # 曲线下面积计算
    auc = simps(pre_list_sorted, x=rec_list_sorted)
    return auc

计算示例：略。

排序

Supearman相关系数

def spearman(true_labels, predict_labels):
    """
    :param true_labels: 真实样本标签。
    :param predict_labels: 对应索引的预测样本标签。
    :return: Spearman系数。
    """
    return spearmanr(true_labels, predict_labels)

计算示例：
true_labels = [0.9, 0.6 ,0.3]
predict_labels = [0.6, 0.4, 0.5]
真实标签的排序等级顺序为：[1, 2 ,3] ；预测标签排序等级为：[1, 3, 2]。
根据简化公式：

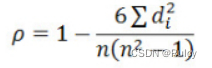
di表示第i项的位序等级差，即d = [0, 1, 1]。
Spearman计算为：1-62/3(9-1)=0.5。

NDCG

def getDCG(scores):
    """
    :param scores: 排序结果的真实相关性分数。真实相关性分数靠前的样本，增益（Gain）更高。当前scores中取值为 3、2、1。
    :return: DCG。
    """
    # DCG。考虑顺序，使排名靠前的增益更高。
    scores = np.array(scores)
    return np.sum(
        np.divide( scores, np.log2(np.arange(scores.shape[0], dtype=np.float32)+2) ),
        dtype=np.float32)

def getNDCG(true_labels, predict_labels):
    """
    :param true_labels: 真实标签。
    :param predict_labels: 预测标签。
    :return: NDCG。
    """
    # 计算IDCG
    idcg = getDCG(sorted(true_labels,reverse=True))
    # 获得当前预测标签下的样本排序。
    suppport_for_relevance = [(true_label,predict_label) for true_label,predict_label in zip(true_labels,predict_labels)]
    suppport_for_relevance = sorted(suppport_for_relevance, key=lambda x: x[1], reverse=True)
    # 计算当前预测排序结果下的DCG。
    sort_relevance = [i[0] for i in suppport_for_relevance]
    dcg = getDCG(sort_relevance)
    return dcg/idcg

计算示例：
true_labels = [0.9, 0.6 ,0.3]
predict_labels = [0.6, 0.4, 0.5]
预测标签下的索引排序为[1, 3, 2]，对应的相关性得分为[0.9, 0.3, 0.6]。
DCG = 0.9/log2(2)+0.3/log2(3)+0.6/log2(4) = 1.3892
IDCG = 0.9/log2(2)+0.6/log2(3)+0.3/log2(4) = 1.4286
NDCG = DCG/IDCG = 0.9725

mAP

def AP(true_labels, predict_labels):
    """
    :param true_labels: 真实样本标签。
    :param predict_labels: 对应索引的预测样本标签。
    :return: Average Precision。
    """
    R = len(true_labels)
    sorted_indexes = sorted(range(len(predict_labels)), key=lambda x: predict_labels[x], reverse=True)
    TP = 0
    P = 0 # @N的N。
    average_precision = 0
    for i in sorted_indexes:
        P += 1
        # 相关性3（pos样本）定义为正样本
        if true_labels[i]==3:
            TP += 1
        average_precision += TP/P*(true_labels[i]-1)/2
    average_precision/=R
    return average_precision

计算示例：
true_labels = [3, 2, 1]
根据公式将true_label归一化到了[1, 0.5, 0]，作为相关性得分。
predict_labels = [0.6, 0.4, 0.5]，根据预测标签排序后的真实标签相关性得分为[1, 0, 0.5]
将标签3视为正样本，则对应索引的正负样本为[1, 0, 0]。
预测标签下的索引排序为[1, 3, 2]，对应的precision@1/2/3为[1, 0.5, 1/3]。
AP = 1/3 * （11 + 00.5 + 0.5* 1/3） = 0.3889