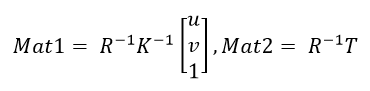转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn]
由于复制过来,如果有格式问题,推荐大家直接去我原网站上查看:
相机模型与坐标转换 - 生活大爆炸
目录
- 经纬度坐标系 转 地球直角坐标系
- 大地直角坐标系 转 经纬度坐标系
- 地理坐标系 转 大地直角坐标
- 机体坐标系 转 地理坐标系
- 相机坐标系 转 机体坐标系
- 图像坐标系 转 像素坐标系
- 相机坐标系 转 图像坐标系
- 世界坐标系 转 相机坐标系
- 世界坐标系 转 像素坐标系
- 透视变换下的坐标转换
-
坐标系系统
- 通用横轴墨卡托UTM
-
坐标转换公式
- WGS84 <–> UTM
- 坐标转换软件
- 三维画图软件
- 测试代码
- 资料推荐
- 题外话
7个坐标系:
- 机体坐标系:单位m,是以载机位置为原点建立的直角坐标系,X轴指向机头方向,Z轴指向载机垂直向下。即带姿态。
- 地理坐标系:单位m,以载机位置为原点建立的NED北东地坐标系
- 大地直角坐标系:单位m,根据参考椭球面建立的笛卡尔直角坐标系,原点为参考椭球面的中心点,Z轴由原点指向地球北极; X轴由原点指向本初子午圈与赤道圈在椭球面上的交点;
- WGS84坐标系:与大地直角坐标系一样,只是采用纬度(M)、经度(L)和大地高(H)表示空间中任一点位置。
- 像素坐标系:单位pixel,相机的成像平面,原点在图像的左上方,u轴向右,v轴向下,像素坐标系的单位是像素(pixel),也就是分辨率。
- 图像坐标系:单位mm,和像素坐标系在同一个平面上,原点是相机光轴与成像平面的交点,通常情况下是成像平面的中点或者叫principal point。单位为物理单位。
- 相机坐标系:单位m,原点是光心,x和y轴与像素坐标系u轴和v轴平行,z轴为相机的光轴。光心到像素平面的距离为焦距f。相机坐标系上的点和成像平面坐标系上的点存在透视投影关系。

无人机 经纬度坐标系 转 大地直角坐标系:

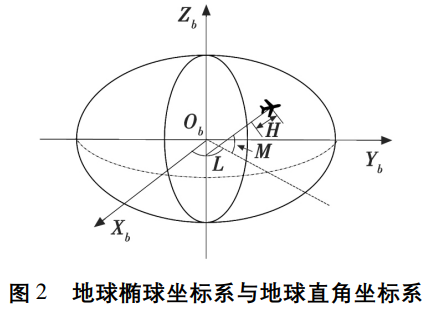

e 表示地球椭球第一偏心率; N 表示无人机所处
位置的卯酉圈曲率半径。分别表示为:

半长轴
RE = 6378137 m,半短轴 RP = 6356752 m
大地直角坐标系 转 经纬度坐标系
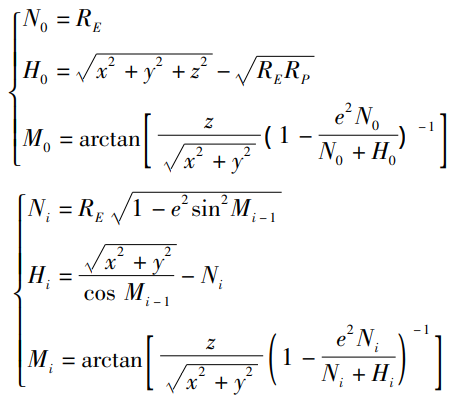

规定北半球纬度为正,南半球纬度为负; 东经为正,西经为负。迭代 4 ~ 5 次即可保证目标大地高的计算精度达到 0.001 m,目标纬度计算精度达到 0.00001°。
地理坐标系 转 大地直角坐标系
旋转平移矩阵:
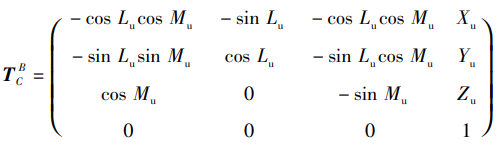
机体坐标系 转 地理坐标系

上式我退出了发现好像有問題的,大家可再确认下:
-cos(yaw)*cos(pitch) 應該是 cos(yaw)*cos(pitch) sin(yaw)*sin(pitch) 應該是 sin(yaw)*cos(pitch)航向 ψ:北偏东为正
俯仰 λ:抬头为正
横滚θ:右倾斜为正
参考转换顺序:
进一步的解释:
矩阵选择:
对右手系而言,定义的正向转动为绕旋转轴的逆时针方向,所以当作用对像(或叫旋转对象)为坐标系中的点或者向量时,应该选用公式(2),但是当旋转的对象是坐标系本身(该坐标系应为参考坐标系),那么应该采用公式(1);反之,在左手系中,定义的正向为顺时针方向,则应该选用相反的公式。
【我们这里是 => 右手坐标系+旋转坐标系本身】
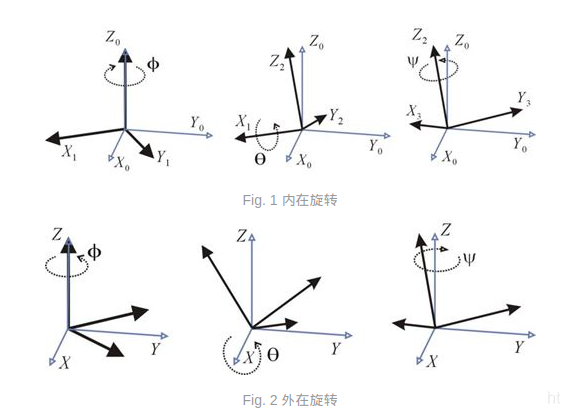
- 旋转顺序:外旋(z->y->x)、内旋(x->y->z)
- 根据每次旋转是绕旋转之后的轴旋转,还是固定轴旋转,将欧拉角分为内旋(intrisic roatation)和外旋(extrinsic rotation)
- R外=R(Z)R(Y)R(X)
- R内=R(α)R(β)R(γ)

- 姿态的变换是相对模型本体的,是内旋,这是不容置疑的,即为偏航-俯仰-滚转。
- 我们需要注意的是,矩阵乘法是外旋。当我们通过矩阵对模型进行姿态变化时,正确的操作是先滚转,再俯仰,最后偏航。
- 但是为什么先滚转就是对的呢,我的理解是这样的,滚转首先肯定是绕机头轴向的滚转才有实际意义,假如我们先绕y偏航45度,然后绕z或x俯仰,最后发现最后那个轴转都不是正确的滚转。
- (以上原贴已404。。。就不贴了)
- 绕大地坐标系旋转(它不动)是矩阵依次右乘,即zyx。
- 绕载体坐标系旋转(它不动)是矩阵依次左乘,即XYZ。
- 内在旋转与外在旋转的转换关系:互换第一次和第三次旋转的位置则两者结果相同。
- 右手系是逆时针为正,左手系是顺时针为正。
相机坐标系 转 机体坐标系

α,β 分别为光电平台采集图像时的方位角与高低角;
注意,上式是默认旋转(-α,-β ),所以注意符号啊。。。
图像坐标系 转 像素坐标系
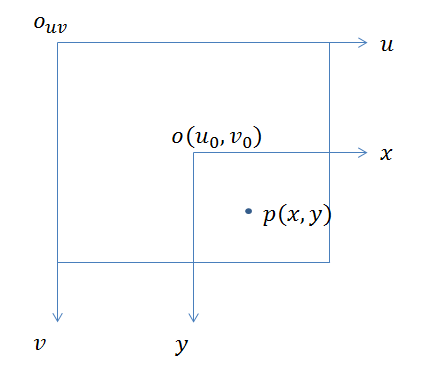

p对应的成像平面坐标为(x,y),dx和dy表示图像中每个像素在成像平面中的物理尺寸。成像平面的原点在像素坐标系中的坐标为(u0,v0)。
相机坐标系 转 图像坐标系


参考Zc计算:
Zc是目标在相机坐标系在Z轴的投影。
世界坐标系 转 相机坐标系

世界坐标系 转 像素坐标系

内参数矩阵K是固定值,由相机标定后确定;外参数矩阵T每张图都不一样,需要提供。
从世界坐标系到像素坐标系之间的转换关系可知,已知世界坐标系下的三维点坐标,只要已知内外参矩阵,就可以求得像素坐标。而如果已知像素坐标,即使已知内外参矩阵,其世界坐标下的三维点也不是唯一确定的,而是空间的一条直线。即单目相机只能测平面信息,而不能获取深度信息。
透视变换下的坐标转换
以上都是刚体变换,但实际摄像头倾斜情况下,会存在透视变换。

以下内容来自“ 参考文献1”:
在无人机目标定位过程中,EOSTP跟踪模块通过伺服调节摄像机的方位角和仰角,以保证目标点落在摄像机视场 中心附近。 因此,相机的视距可以有效地反映目标点与无人机之间的位置关系。
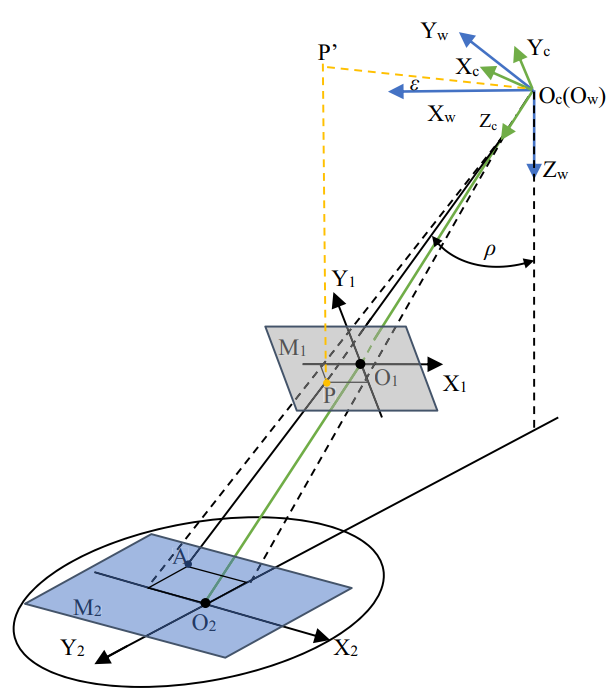
LOS的角度($\rho,\epsilon$)定义如图4所示,$\rho$为LOS矢量与世界坐标系z轴的夹角,$\epsilon$为LOS矢量在$X_wO_wY_w$平面上的投影与世界坐标系x轴的夹角。 $q$和$\epsilon$由无人机的姿态、相机的方位角和仰角决定。
在图4中,$M_1$和$M_2$分别表示图像平面和物平面。 在M1中,O为图像平面与相机光轴的交点,$O_1X_1$、$O_1Y_1$为图像平面水平和垂直方向的两个轴。P为目标点A在像平面上的投影点,其图像物理坐标为$(x_p, y_p)$。$P ^ { \prime }$是P在$O_w-X_wY_w$平面上的投影。在M2中,$O_2$是相机光轴与物体平面的交点。$O_2X_2$和$O_2Y_2$分别是$O_1X_1$和$O_1Y_1$在$M_2$平面上的投影。$O_c$为相机的镜头中心,$O_cO$为焦距f。$O_c-X_cY_cZ_c$为相机坐标系,$O_w-X_wY_wZ_w$为世界坐标系。
向量$O_cP$可以在$O_c-X_cY_cZ_c$坐标系下表示为$v _ { c } = ( x _ { p } , y _ { p } , f ) ^ { T }$。
设$O_cP$在$O_w-X_wY_wZ_w$坐标系下表示为$v _ { c w }$,则$v _ { c w } = R o t _ { B } ^ { W } ( \phi , \gamma , \theta ) \cdot R o t _C^ { B } ( \phi , \gamma , \theta ) \cdot { v_c }$,其中$ R o t _C^ { B } ( \phi , \gamma , \theta )$为摄像机坐标系到无人机坐标系的旋转矩阵,$R o t _ { B } ^ { W } ( \phi , \gamma , \theta ) $为无人机坐标系到世界坐标系的旋转矩阵。 无人机的偏航角$\phi$、俯仰角$\gamma$和滚转角$\theta$都可以通过IMU进行测量。
设$t _ { z w } = ( 0 , 0 , 1 ) ^ { T }$为坐标轴$O_wZ_w$上的单位向量,则$\cos ( < v _ { c w } , t _ { z w } > ) = \frac { v _ { c w } \cdot t _ {z w } } { | v _ { c w } | |t_{ zw }| }$
如果$O_cA$和$O_wZ_w$的夹角是$\rho$,那么:$\rho = \arccos ( < v _ { cw } , t _ { w } >)\ \ \ \rho \ \ in\ [ 0 , \pi / 2 )$
向量$O_cP$在平面$O_cX_cY_c$上的投影为$O_cP ^ { \prime }$, $O_cP ^ { \prime }$在$O_cX_cY_cZ_c$坐标系下可以表示为$v _ { b } = ( x _ { p } , y _ { p } , 0 ) ^ { T }$。
设$O_cP^ { \prime }$在$O_wX_wY_wZ_w$坐标系下表示为$v _ { b w }$,则: $v _ { b w } = R o t _ { B } ^ { W } ( \phi , \gamma , \theta ) \cdot R o t _ { C } ^ { B } ( \phi , \gamma , \theta ) \cdot { v _b }$
设$t _ { x w } = ( 1 , 0 , 0 ) ^ { T }$为坐标轴$O_wX_w$上的单位向量。 则: $\cos ( < v _ { b w } , t _ { x w } > ) = \frac { v _ { b w } \cdot t _ { x w } } { | v _ { b w } | | t _ {x w}| }$
如果$O_cP^ { \prime }$和$O_wX_w$的夹角为$\epsilon$,则$e = \arccos ( < { v }_ { b w } , t _ { x w } > )\ \ \ \epsilon\ \ in ( 0 , 2 \pi ]$
(就没了???O2平面的呢???)
参考:
1、无人机单载荷目标检测及定位联合实现方法_王宁
2、基于电光稳定和跟踪平台的无人驾驶飞行器的目标位置
3、针孔相机模型 | 一索哥传奇
4、https://python.iitter.com/other/197329.html
坐标系系统
常用坐标系椭球参数
| 克拉索夫斯基椭球 | 1975国际椭球 | WGS84椭球 | 国家2000坐标系椭球 | |
| 长半轴(a) | 6378245 | 6378140 | 6378137 | 6378137 |
| 短半轴(b) | 6356863.0187730473 | 6356755.288157528 | 6356752.3142451795 | 6356752.3141403558 |
扁率:$$\partial=\frac{a-b}b$$
第一偏心率:$$e=\frac{\sqrt{a^2-b^2}}a$$
第二偏心率:$$e^{’}=\frac{\sqrt{a^2-b^2}}b$$
通用横轴墨卡托UTM
- 统一横轴墨卡托投影系统(Universal Transverse Mercator,UTM)
- 60个精度区,其中 58 个区的东西跨度为 6°。
- 20个纬度区,每个区的南北跨度为 8°。
- 坐标格式:经度区纬度区以东以北,其中以东表示从经度区的中心子午线的投影距离,而以北表示距离赤道的投影距离。单位为米。
-
坐标轴规定:
- X:从西向东递增,称为“东移”
- Y:从南到北递增,称为“北”
- Z:从下到上增加,称为“高程”
- B:从正X轴绕Z轴顺时针增大
NED
-
北东地坐标系(导航坐标系)
- N——北轴指向地球北;
- E——东轴指向地球东;
- D——地轴垂直于地球表面并指向下。

坐标转换公式
WGS84 <–> UTM
https://en.wikipedia.org/wiki/Universal_Transverse_Mercator_coordinate_system
坐标转换软件
COORD GM2.0 (可转2000坐标)终结版.zip - 蓝奏云

三维画图软件
Vectary - Build interactive 3D and AR solutions online
测试代码
TODO
资料推荐
1、这个PPT很不错:Camera Calibration
题外话
1、注意OpenCV中图像的x、y和w、h的顺序。
# 图像点坐标顺序:x, y, z; 且:
# row = height = Point.y
# col = width = Point.x
# 图像宽高顺序:height, width, channel; 且:
h = img.shape[0] - 1 # 高度
w = img.shape[1] - 1 # 宽度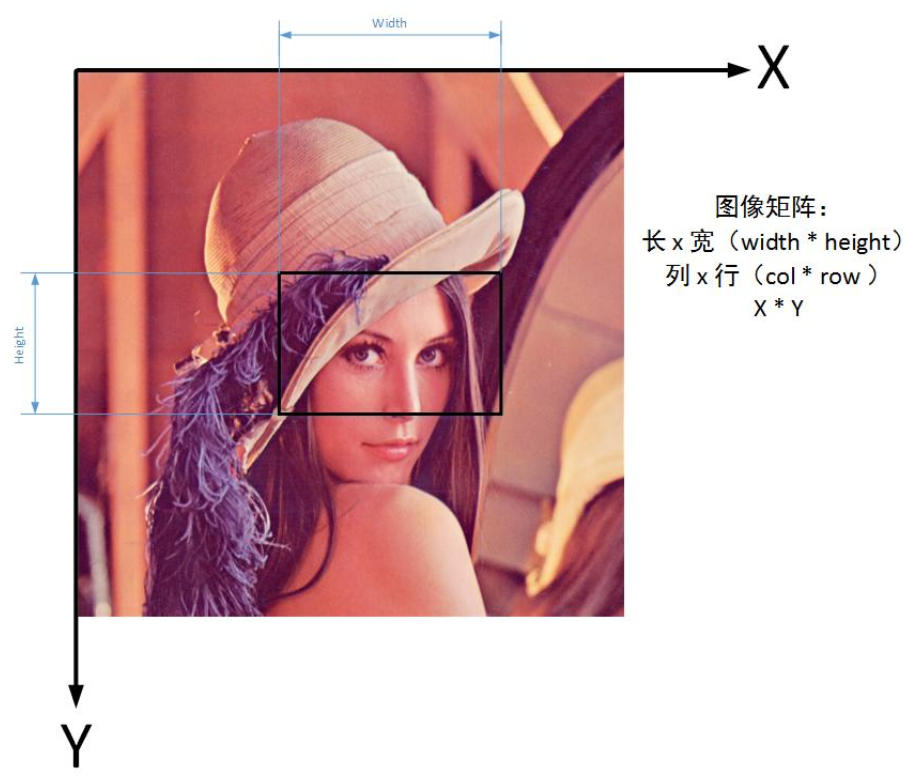
0