原题链接:https://www.acwing.com/problem/content/5474/
题目描述:
奶牛贝茜和奶牛贝蒂各有一个整数数对。
每个数对都包含两个 1∼9 之间的不同整数。
这两个数对恰好包含一个公共数,即恰好有一个整数同时包含于这两个数对。
初始时,贝茜和贝蒂都只知道自己拥有的数对,而不清楚对方拥有的数对。
它们希望通过网络交流来获知彼此数对的公共数。
但是,它们清楚所有交流信息一定会被农夫约翰截获,且约翰也知道这两个数对恰好包含一个公共数。
为了让截获到交流信息的约翰无法获知这个公共数,它们决定采用如下方式加密信息。
贝茜会准备 n 个两两不同的数对,这些数对均包含两个 1∼9 之间的不同整数,其中一个数对恰好是它拥有的数对,它会将这些数对全部发送给贝蒂。
贝蒂会准备 m 个两两不同的数对,这些数对均包含两个 1∼9 之间的不同整数,其中一个数对恰好是它拥有的数对,它会将这些数对全部发送给贝茜。
当然,约翰会将这些数对(以及是谁发送的)全部获知。
请你对给定信息进行判断,并按要求输出:
- 如果这些信息足以令约翰准确地推断出公共数字,则输出这个公共数字。
- 如果这些信息不足以令约翰准确地推断出公共数字,但是不论两头奶牛各自拥有哪个数对,都足以令两头奶牛都准确地推断出公共数字,则输出
0。 - 以上都不是,则输出
-1。
输入输出描述:
输入格式
第一行包含两个整数 n,m。
第二行包含 n 个两两不同的数对,这些数对均包含两个 1∼9 之间的不同整数,表示贝茜准备的数对。
第三行包含 m 个两两不同的数对,这些数对均包含两个 1∼9 之间的不同整数,表示贝蒂准备的数对。
在本题中,(1,2) 和 (2,1) 视为同一数对。
数据保证双方拥有的数对包含于各自给出的数对当中,且双方拥有的数对恰好包含一个公共数。
输出格式
按照题目要求,输出公共数字或 0 或 -1。
数据范围
前 4 个测试点满足 1≤n,m≤3。
所有测试点满足 1≤n,m≤12
输入样例1:
2 2
1 2 3 4
1 5 3 4
输出样例1:
1
输入样例2:
2 2
1 2 3 4
1 5 6 4
输出样例2:
0
输入样例3:
2 3
1 2 4 5
1 2 1 3 2 3
输出样例3:
-1解题思路:
这个题目的特点就是题目比较长,理解题意比较困难,感觉就是一个阅读理解题,题读懂了就是很简单的一道题,读不懂就会一直wa,这个题目是很容易wa的,我们对三种情况进行分开分析。
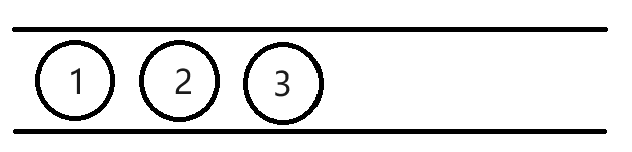
首先我们考虑第一种情况,什么时候农夫约翰可以截取到他们的各自数对的公共数呢,我们来画一个图分析一下,分析图如下所示:

如上图所示,上边是a的数对,下边是b的数对,我们对所有数对进行编号,同时红色线连接表示俩个数对恰好有一个公共数,那么什么时候农夫约翰可以截取到俩人的数对的公共数呢,肯定是当a中的每一个数对和b中的数对的所有有红色线连接数对的公共数只有一种,此时可以通过a连接到b的红线知道他们俩个人数对的公共数,或者是当b中的每一个数对和a中的数对的所有有红色线连接数对的公共数只有一种,此时可以通过b连接到a的红线知道他们俩个人数对的公共数。
当上面的第一种情况不成立时,下面分析第二种情况,什么时候俩头牛都可以知道他们的公共数呢,上面图中,1分别和5,6,7都有一个公共数,当这三个公共数不相同时,那么如果a拿出编号为1的数对时,此时a无法知道俩人的公共数是啥,只有当三个数都一样时,a才能知道公共数是啥,也就是说只有a中的每一个数对,该数对和连出去的红线对应数对的公共都一样,此时a才能推断出俩人的公共数,否咋a无法推断出俩人的公共数,b同理。
上述第二种情况不满足,就是第三种情况了,直接输出-1。
时间复杂度:O(n+m)。
空间复杂度:O(n+m)。
cpp代码如下:
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=100;
int n,m;
int a[N],b[N];
void solve(int a[],int b[],int n,int m,unordered_map<int,int>&mp,bool& ok)
{
for(int i=1;i<=n*2;i+=2)
{
int x1=a[i],y1=a[i+1];
int v1=0,v2=0;
for(int j=1;j<=m*2;j+=2)
{
int x2=b[j],y2=b[j+1];
if(x1==x2 && y1!=y2){
v1++;
}
if(x1!=x2 && y1==y2){
v2++;
}
if(x1==y2 && y1!=x2){
v1++;
}
if(x1!=y2 && y1==x2){
v2++;
}
}
if(v1!=0 && v2!=0){ //当出现某个数对连出去的红线,出现了俩种公共线,说明情况二肯定是不满足的
ok=true;
}
if(v1!=0){
mp[x1]++;
}
if(v2!=0){
mp[y1]++;
}
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n*2;i++)cin>>a[i];
for(int i=1;i<=m*2;i++)cin>>b[i];
unordered_map<int,int>mp1,mp2; //mp1记录a连出去的红线对应数对的公共数,mp2记录b的。
bool ok1=false,ok2=false; //ok1记录a每个数对连出去的红线对应数对的公共数是否相同,b同理对应b连出去红线到a
solve(a,b,n,m,mp1,ok1),solve(b,a,m,n,mp2,ok2); //对a,b分别进行处理
if(mp1.size()==1 || mp2.size()==1){ //情况一
if(mp1.size()==1)cout<<mp1.begin()->first<<endl;
else cout<<mp2.begin()->first<<endl;
}else if(!ok1 && !ok2){ //情况2
cout<<0<<endl;
}else { //情况3
cout<<-1<<endl;
}
return 0;
}