适用平台:Matlab2023版及以上
雪消融优化算法(Snow Ablation Optimizer,SAO),于2023年6月发表在SCI、中科院1区顶级期刊《Expert Systems With Applications》上。该算法刚刚提出,目前还没有套用这个算法的文献!在此基础上,我们进一步对SAO雪消融算法进行高创新性改进!提出融合佳点集策略和周期振荡突变策略的GVSAO优化算法,创新性极高!感兴趣的小伙伴可以直接发表高水平的小论文哦
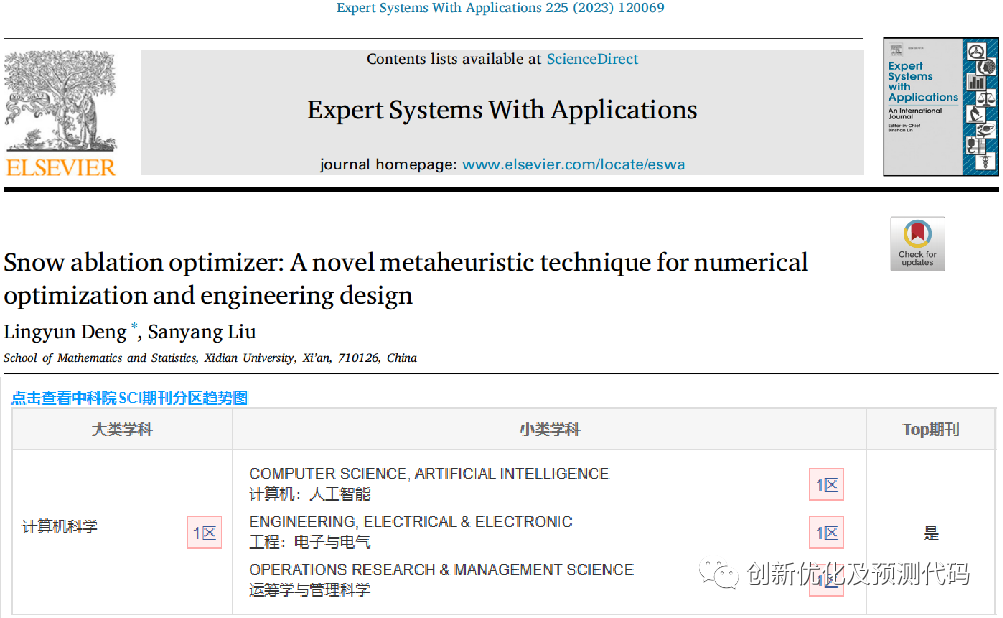
SAO文献解读:
这篇论文提出了一种新颖的元启发式算法,命名为雪消融优化(Snow Ablation Optimizer,SAO),用于数值优化和工程设计。SAO算法主要模拟雪的升华和融化行为,以在解空间中实现开发和探索之间的权衡,并避免过早的收敛。
通过使用29个典型的CEC2017无约束基准问题和22个CEC2020真实约束的优化问题进行验证,还与传统的AO、MVO、EO、AVOA、HHO、PSO-sono、SHADE、LSHADE-SPACMA,验证了SAO的优化能力。此外,为了进一步验证其优势,作者还将SAO应用于提取光伏系统的核心参数。结果表明,开发的SAO比其他先进的优化方法表现更好。
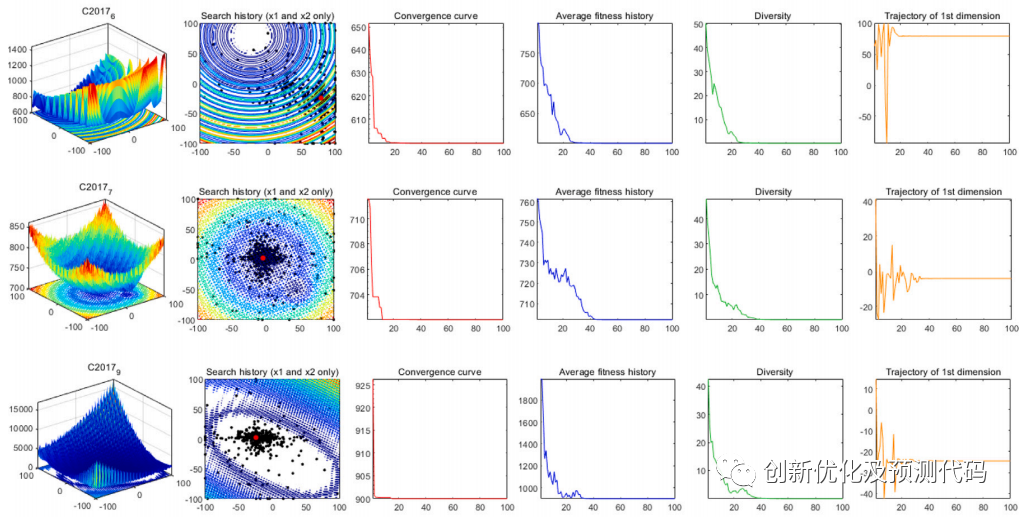
GVSAO创新性算法改进:
①改进点一:佳点集是由我国数学家华罗庚等提出,其原理为均匀分布初始搜索个体,在初始化过程中可增加种群的多样性,有利于摆脱局部最值的吸引。
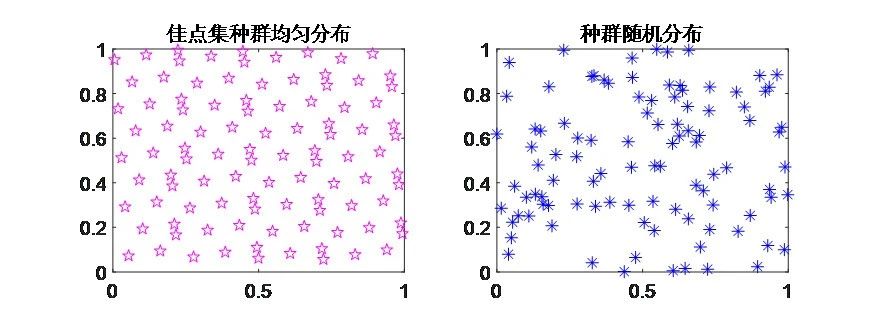
②改进点二:大量文献采用的传统改进策略,例如:混沌映射、柯西变异、高斯变异、随机游走、差分变异、反向学习、莱维飞行等等。然而,这些策略已经被过度使用,司空见惯,难以产生新颖的效果,导致文章缺乏独特性。本文采用的周期振荡突变策略较为罕见,在不增加计算负担的情况下显著提高了模型的收敛速度,为文章注入了极高创新性。
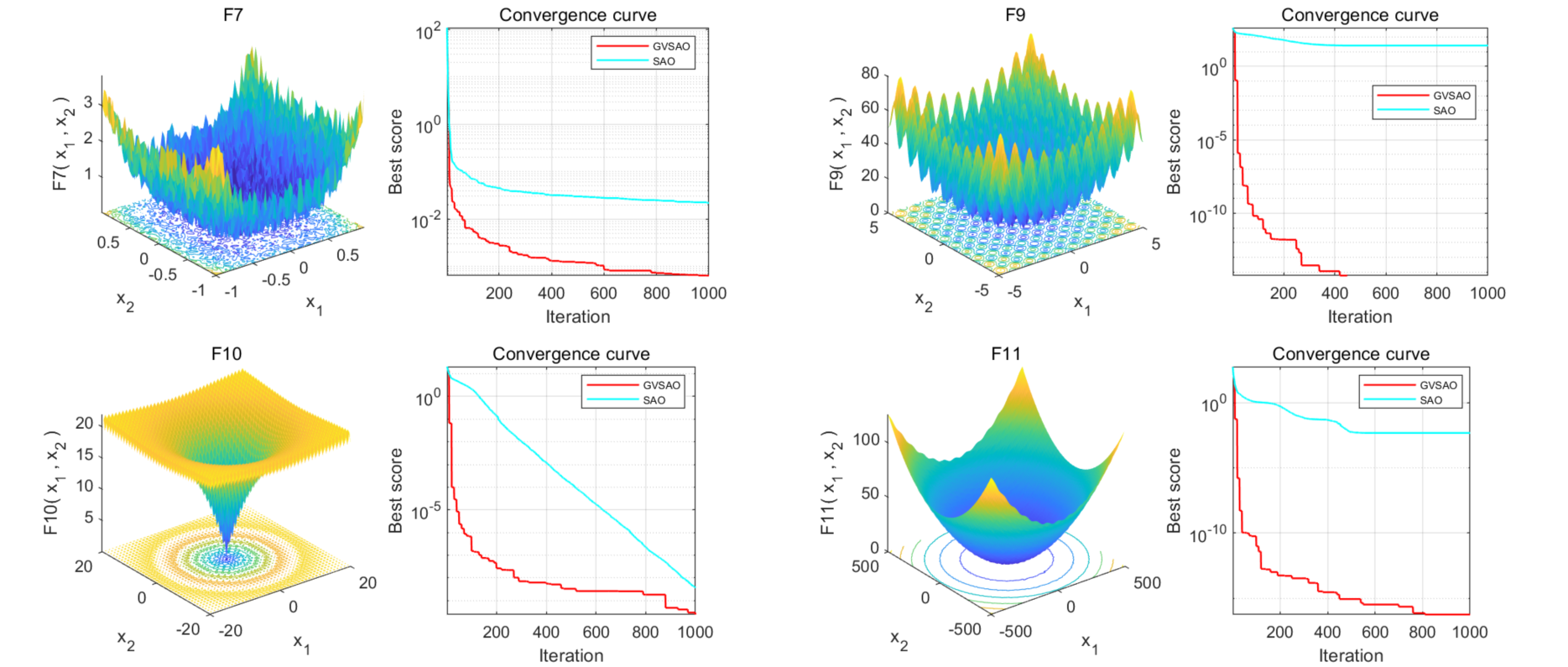
GVSAO算法的创新点主要体现在以下6个方面:
-
佳点集初始化策略:在初始化过程中,种群均匀分布,可增加种群的多样性,有利于摆脱局部最值的吸引。
-
双重种群机制:SAO算法引入双重种群机制,将种群分为两个子群,分别负责探索和利用,以实现在解决方案空间中的平衡。
-
布朗运动探索策略:在探索阶段,算法采用布朗运动模拟蒸汽的不规则运动,使搜索代理具有高度分散的特征,从而探索潜在区域。
-
度日法利用策略:在利用阶段,SAO采用度日法模拟雪融过程,鼓励搜索代理在当前最佳解决方案附近寻找高质量解。
-
整体位置更新方程:SAO算法采用一种整体位置更新方程,结合探索和利用策略,以及种群动态变化,优化每个个体的位置。
-
周期振荡突变策略:设计这种突变策略的目的是抓住收敛的大趋势,从局部陷阱中逃脱并获得正确的搜索模式。
总结:GVSAO算法相较于其他优化算法的优势在于其独特的双重种群机制、高效的探索与利用策略以及灵活的位置更新方程。这些特点使其在处理复杂优化问题时表现出更好的平衡能力、搜索效率和适应性,特别是在多峰值和高维问题上。此外,GVSAO算法的物理背景和数学原理为解决实际问题提供了新的视角。
CNN-BiGRU-SelfAttention模型的创新性:
①结合卷积神经网络 (CNN) 和双向门控循环单元 (BiGRU):CNN 用于处理多变量时间序列的多通道输入,能够有效地捕捉输入特征之间的空间关系。BiGRU 是一种能够捕捉序列中长距离依赖关系的递归神经网络。通过双向性,BiGRU 可以同时考虑过去和未来的信息,提高了模型对时间序列动态变化的感知能力。
②引入多头自注意力机制 (Multihead Self-Attention): 多头自注意力机制使得模型能够更灵活地对不同时间步的输入信息进行加权。这有助于模型更加集中地关注对预测目标有更大影响的时间点。自注意力机制还有助于处理时间序列中长期依赖关系,提高了模型在预测时对输入序列的全局信息的感知。
优化套用:基于融合佳点集策略和周期振荡突变策略的雪消融优化算法(GVSAO)、卷积神经网络(CNN)和双向门控循环单元 (BiGRU)融合多头自注意力机制的超前24步多变量时间序列回归预测算法。
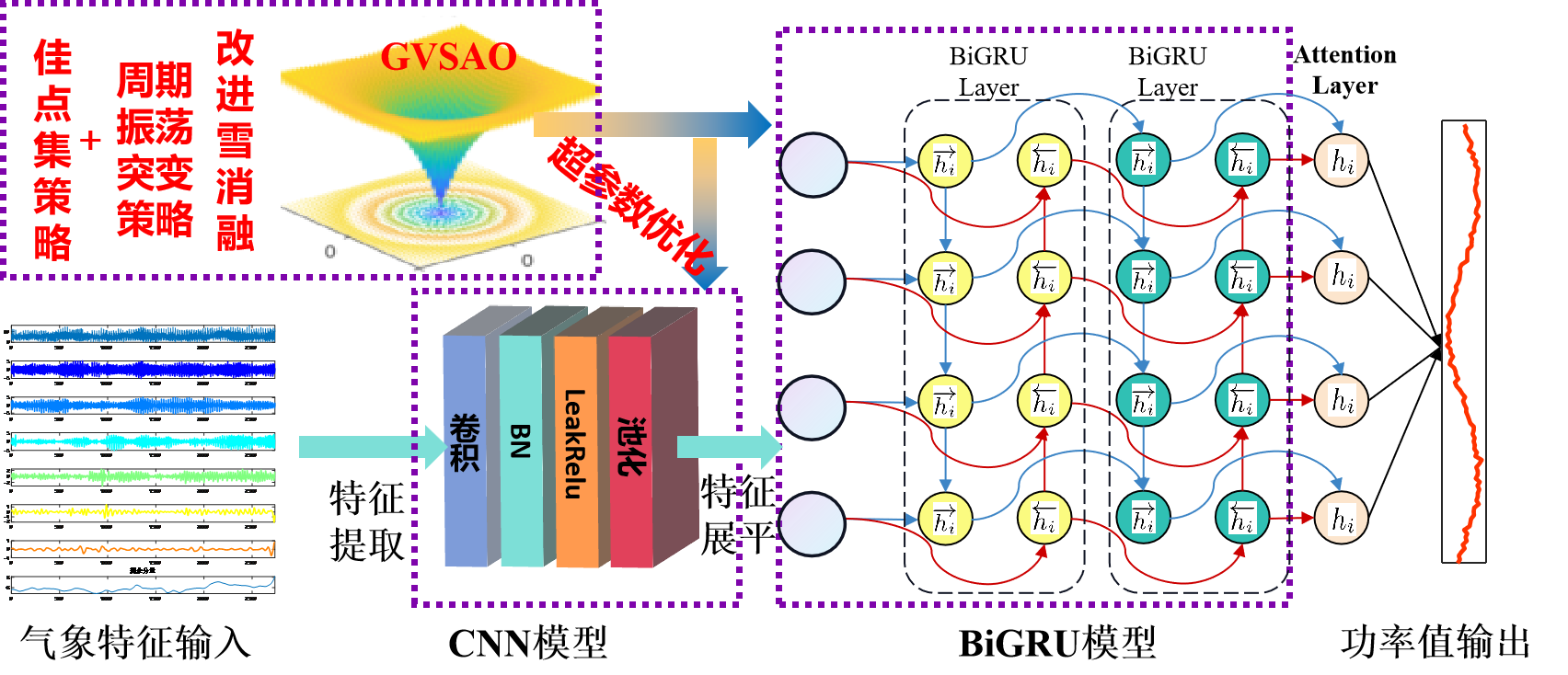
功能:
-
多变量特征输入,单序列变量输出,输入前一天的特征,实现后一天的预测,超前24步预测。
-
通过GVSAO优化算法优化学习率、卷积核大小、神经元个数,这3个关键参数,以最小MAPE为目标函数。
-
提供损失、RMSE迭代变化极坐标图;网络的特征可视化图;测试对比图;适应度曲线(若首轮精度最高,则适应度曲线为水平直线)。
-
提供MAPE、RMSE、MAE等计算结果展示。
适用领域:风速预测、光伏功率预测、发电功率预测、碳价预测等多种应用。
数据集格式:
前一天18个气象特征,采样时间为24小时,输出为第二天的24小时的功率出力,也就是18×24输入,1×24输出,一共有75个这样的样本。
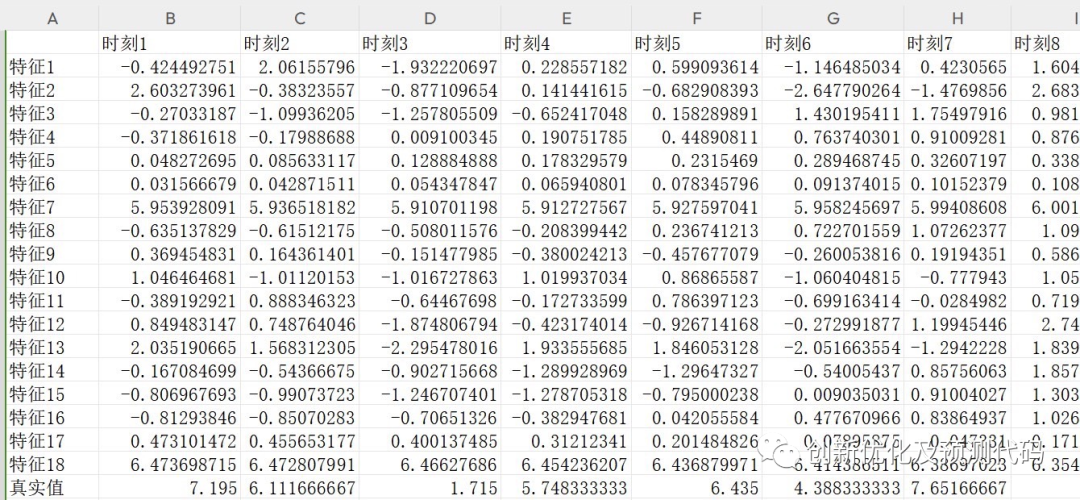
预测值与实际值对比结果:
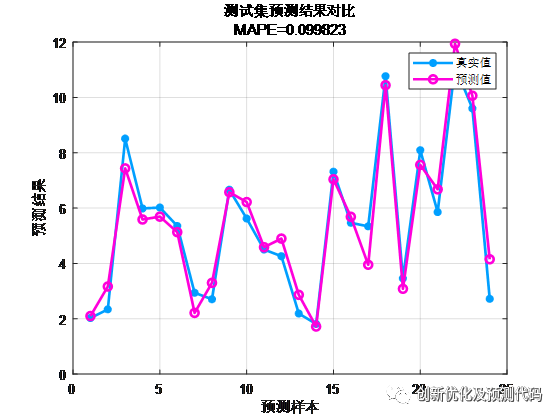
训练特征可视化:
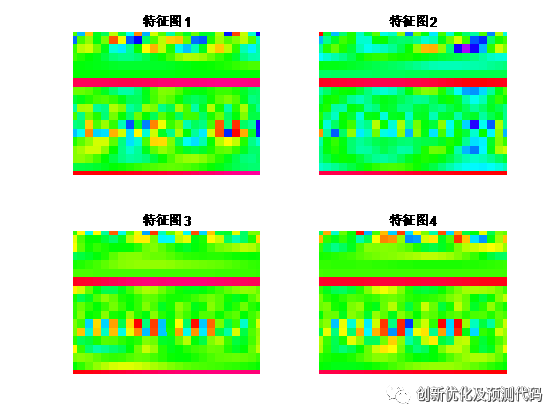
训练误差曲线的极坐标形式(误差由内到外越来越接近0):
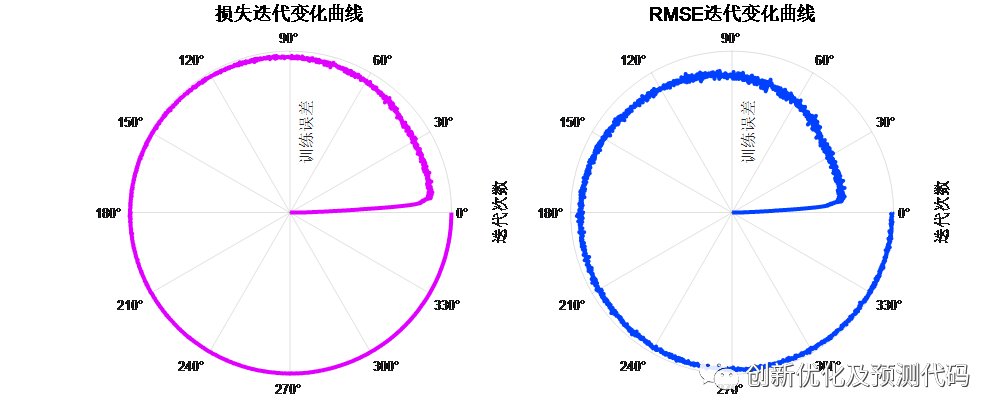
适应度曲线:
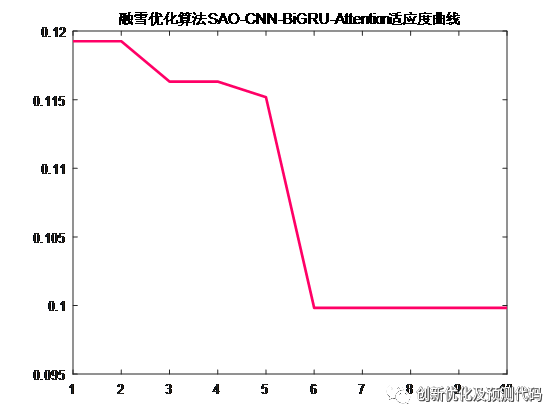
部分代码:
完整代码:https://mbd.pub/o/bread/ZZuVmptw
%% 优化算法信息
SearchAgents_no = 4; %% 搜索个体的数量(2的倍数,且大于3)
Max_iter = 10; %% 最大迭代次数
lb = [0.001, 2, 100]; %% 寻优参数下限 [学习率, 卷积核大小, 神经元数量];
ub = [0.01, 5, 120]; %% 寻优参数上限 [学习率, 卷积核大小, 神经元数量];
dim = 3; %% 有几个需要优化的参数就是几维
fobj = @objectiveFunction;%% 目标函数
%% 融雪优化算法SAO优化超参数
[Leader_score, Leader_pos, Convergence_curve, bestPred, bestNet, bestInfo] = GVSAO(SearchAgents_no, Max_iter, lb, ub, dim, fobj);
%% 优化结果导出
Best_Cost = Leader_score; %% 最佳适应度
Best_Solution = Leader_pos; %% 最佳网络参数
bestPred = bestPred; %% 最佳预测值
bestNet = bestNet; %% 最佳网络
bestInfo = bestInfo; %% 最佳训练曲线
% 显示优化结果
disp(['优化所得参数分别为' num2str(Leader_pos)]);
%% 绘制适应度曲线
figure
plot(Convergence_curve,LineWidth=2,Color=[1 0 0.4]); %% 颜色映射为玫红色R为1; G为0; B为0.4
title('改进融雪优化算法GVSAO-CNN-BiGRU-Attention适应度曲线')
%% %%%%%%%%%%%%%%%%%%% 绘制优化迭代曲线 %%%%%%%%%%%%%%%%%%%%%%%
%% 损失迭代变化曲线
num_iterations = size(bestInfo.TrainingLoss,2);
train_curve = smooth((bestInfo.TrainingLoss),2) ;%% 损失曲线
% 定义角度范围(由内到外)
theta = linspace(0, 2*pi, num_iterations); % 用于闭合圆形
% 转换训练曲线数据为极坐标系下的数据(半径由高到低)
rho = max(train_curve) - train_curve;
% 绘制极坐标图
figure;
polarplot(theta, rho, 'Color', [0.875 0 1], 'LineWidth', 3);
% 设置极坐标图属性
ax = gca; % 获取当前轴句柄
ax.RAxis.Label.String = '训练误差'; % 设置半径标签
ax.ThetaAxis.Label.String = '迭代次数'; % 设置角度标签
ax.RAxis.Label.FontSize = 12; % 设置标签字体大小
ax.ThetaAxis.Label.FontSize = 12;
ax.RLim = [0, max(rho)]; % 设置半径范围
ax.RTick = [];
title('损失迭代变化曲线', 'FontSize', 14);
%% RMSE迭代变化曲线
num_iterations = size(bestInfo.TrainingRMSE,2);
RMSE_curve = smooth((bestInfo.TrainingRMSE),2) ;%% 损失曲线
% 定义角度范围(由内到外)
theta = linspace(0, 2*pi, num_iterations); % 用于闭合圆形
% 转换训练曲线数据为极坐标系下的数据(半径由高到低)
rho = max(RMSE_curve) - RMSE_curve;
% 绘制极坐标图
figure;
polarplot(theta, rho, 'Color', [0 0.25 1], 'LineWidth', 3);
% 设置极坐标图属性
ax = gca; % 获取当前轴句柄
ax.RAxis.Label.String = '训练误差'; % 设置半径标签
ax.ThetaAxis.Label.String = '迭代次数'; % 设置角度标签
ax.RAxis.Label.FontSize = 12; % 设置标签字体大小
ax.ThetaAxis.Label.FontSize = 12;
ax.RLim = [0, max(rho)]; % 设置半径范围
ax.RTick = [];
title('RMSE迭代变化曲线', 'FontSize', 14);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 绘制某层的特征图,实现特征可视化
%激活某一层
LayersNeed = activations(bestNet,XTrain,'flatten','OutputAs','channels');% flatten层的特征
% 分析前4个训练样本
figure;
for i = 1:4 % 前4个样本特征图 i的不能超过训练集单元的个数
LayersFeature = reshape(cell2mat(LayersNeed(i,:)),18,[]); %根据analyzeNetwork分析结果,构造合适尺寸的特征图18*24
subplot(2, 2, i); % 创建该层的第i个子图
image(LayersFeature, 'CDataMapping', 'scaled');
colormap(hsv);
xlim([1, size(LayersFeature, 2)]); % 限制坐标轴
ylim([1, size(LayersFeature, 1)]); % 限制坐标轴
axis off; % 关闭坐标轴显示
box on;
title(['特征图', num2str(i)]); % 添加特征图标题
end
%% 测试集结果 % 来自:公众号《创新优化及预测代码》
figure;
plotregression(Ytest,bestPred,['回归图']);
figure;
ploterrhist(Ytest-bestPred,['误差直方图']);
%% 均方根误差 RMSE
error2 = sqrt(sum((Ytest - bestPred).^2)./N);
%%
%决定系数
R2 = 1 - norm(Ytest - bestPred)^2 / norm(Ytest - mean(Ytest))^2;
%%
%均方误差 MSE
mse2 = sum((bestPred - Ytest).^2)./N;
%%
%RPD 剩余预测残差
SE=std(bestPred-Ytest);
RPD2=std(Ytest)/SE;
%% 平均绝对误差MAE
MAE2 = mean(abs(Ytest - bestPred));
%% 平均绝对百分比误差MAPE
MAPE2 = mean(abs((Ytest - bestPred)./Ytest));欢迎感兴趣的小伙伴联系小编或点击代码上方链接获得完整版代码哦~,关注小编会继续推送更有质量的学习资料、文章程序代码~