C++_二叉搜索树

news2024/11/30 0:31:34

目录

1、二叉搜索树的概念

 2、二叉搜索树的插入

3、二叉搜索树的查找

4、二叉搜索树的删除

5、二叉搜索树的拷贝构造与析构

前言：

        二叉搜索树是一颗二叉树，他跟普通的二叉树的区别在于：二叉搜索树的节点是按照特定规则进行摆放的。二叉搜索树的优势在于：无特殊情况下，其增删查改数据的时间复杂度可以达到O(log N)，这个效率相比于线性表的效率，前者明显高出很多。

1、二叉搜索树的概念

        二叉搜索树具备搜索功能的同时还可以通过中序遍历进行排序，因此二叉搜索树也称二叉排序树。他的具体性质如下：

1、左子树所有节点的值都小于根节点的值。

2、右子树所有节点的值都大于根节点的值。

3、左子树和右子树本身也同样满足上面两个性质。

4、树中不能出现相同值的节点。

        二叉搜索树示意图如下：

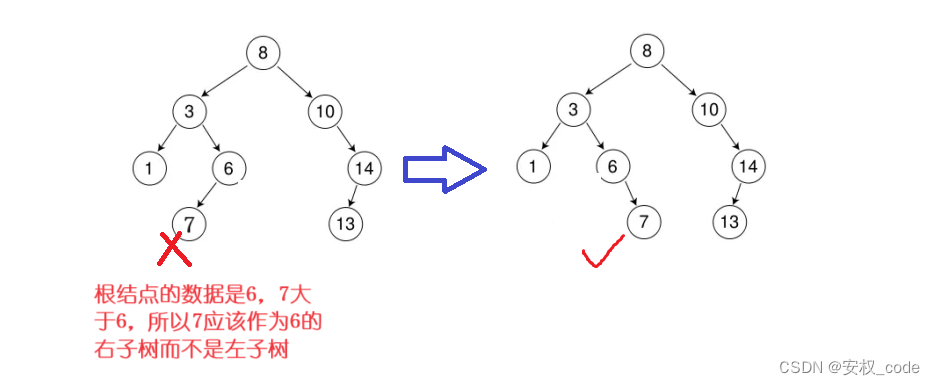
 2、二叉搜索树的插入

        若要插入新的节点，则需遵循二叉树的性质，若插入节点的数值比根结点大则往右子树遍历，若插入节点的数值比根结点小则往左子树遍历，如此反复遍历，直到遇到nullptr，说明已经走到了插入点的位置，插入的时候还需要把该节点和父节点进行连接。若插入的数据和树里数据相同，则不能插入。

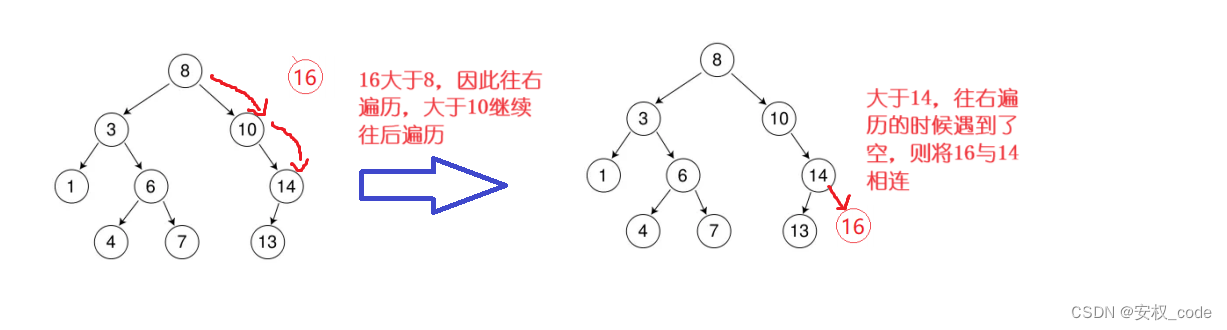
         插入代码如下：

#define _CRT_SECURE_NO_WARNINGS 1

#include<iostream>
using namespace std;

template<class K>
struct BSTree_node//节点对象
{
	BSTree_node<K>* left;
	BSTree_node<K>* right;
	K key;

	BSTree_node(const K& k)
		:left(nullptr)
		, right(nullptr)
		, key(k)
	{}
};

template<class K>
class BSTree//树对象
{
public:
	typedef BSTree_node<K> node;

	void _Insert(const K& k)//子函数，方便外部调用
	{
		Insert(_root, k);
	}
	bool Insert(node*& root, const K& k)//递归实现插入函数
	{
		if (root == nullptr)//找到空处，因为root是引用，因此可以直接插入新节点
		{
			root = new node(k);
			return true;
		}

		//按照左边找小，右边找大遍历树
		if (k > root->key)
		{
			Insert(root->right, k);
		}
		else if (k < root->key)
		{
			Insert(root->left, k);
		}
		else//相同则不会插入
			return false;
	}

	//打印函数
	void _show()
	{
		show(_root);
	}
	void show(node* root)//中序遍历打印
	{
		if (root == nullptr)
		{
			return;
		}

		show(root->left);
		cout << root->key << " ";
		show(root->right);
	}

private:
	node* _root = nullptr;
};

int main()
{
	BSTree<int> bt1;
	int arr[] = { 8,8,3,1,10,6,4,7,14,13 };
	for (auto num : arr)
	{
		bt1._Insert(num);
	}
	bt1._show();
	return 0;
}

        运行结果：

3、二叉搜索树的查找

        二叉搜索树的查找逻辑和插入逻辑相似，从根节点开始找，若要查找的节点数值大于根结点则往右子树遍历，反之往左子树遍历，若找到了则返回真，没找到则返回假。

        查找函数代码如下：

#define _CRT_SECURE_NO_WARNINGS 1

#include<iostream>
using namespace std;

template<class K>
struct BSTree_node//节点对象
{
	BSTree_node<K>* left;
	BSTree_node<K>* right;
	K key;

	BSTree_node(const K& k)
		:left(nullptr)
		, right(nullptr)
		, key(k)
	{}
};

template<class K>
class BSTree//树对象
{
public:
	typedef BSTree_node<K> node;

	void _Insert(const K& k)//子函数，方便外部调用
	{
		Insert(_root, k);
	}
	bool Insert(node*& root, const K& k)//递归实现插入函数
	{
		if (root == nullptr)//找到空处，因为root是引用，因此可以直接插入新节点
		{
			root = new node(k);
			return true;
		}

		//按照左边找小，右边找大遍历树
		if (k > root->key)
		{
			Insert(root->right, k);
		}
		else if (k < root->key)
		{
			Insert(root->left, k);
		}
		else//相同则不会插入
			return false;
	}

	//查找函数
	bool _find(const K& k)
	{
		return find(_root, k);
	}
	bool find(const node* root, const K& k)
	{
		if (root == nullptr)
		{
			return false;
		}
		if (k > root->key)
		{
			find(root->right, k);
		}
		else if (k < root->key)
		{
			find(root->left, k);
		}
		else
			return true;
	}

private:
	node* _root = nullptr;
};

int main()
{
	BSTree<int> bt1;
	int arr[] = { 8,8,3,1,10,6,4,7,14,13 };
	for (auto num : arr)
	{
		bt1._Insert(num);
	}
	cout << bt1._find(10) << endl;//找到了返回1
	cout << bt1._find(1) << endl;//找到了返回1
	cout << bt1._find(100) << endl;//没找到返回0
	return 0;
}

4、二叉搜索树的删除

        删除逻辑较插入和查找更复杂，需要具体分析：删除节点的情况无论如何只有以下四种：

        1、删除节点没有孩子节点，即要删除的节点是叶子节点。

        2、删除节点只有左孩子，即右孩子为空。

        3、删除节点只有右孩子，即左孩子为空。

        4、删除节点即有左孩子也有右孩子。

        一个节点只虽然有以上四种情况，但是删除的时候只需要考虑两种情况：

        情况一：上述情况1、2、3可以综合成一种情况，因为删除该类情况的节点时，只需要把该节点中不为空的孩子节点与该节点的父母节点相连接即可，该方法也可以处理没有孩子节点的情况，举例：如果一个节点的左孩子为空，那么不管右孩子是否为空都将右孩子与该节点的父母节点相连接。

        情况二：上述情况4可以归成情况二，如果删除的节点同时拥有左孩子和右孩子，那么把该节点当作根节点，去该节点的左子树找到一个最大值，或者去该节点的右子树找到一个最小值，然后与该节点进行交换，交换过后要删除的节点就不再是根节点了，也意味着该节点的情况不再符合情况4，而符合上述的情况1、2、3，这时候可以用情况一的处理方式来删除该节点。

        情况一示意图： 

        情况二示意图：

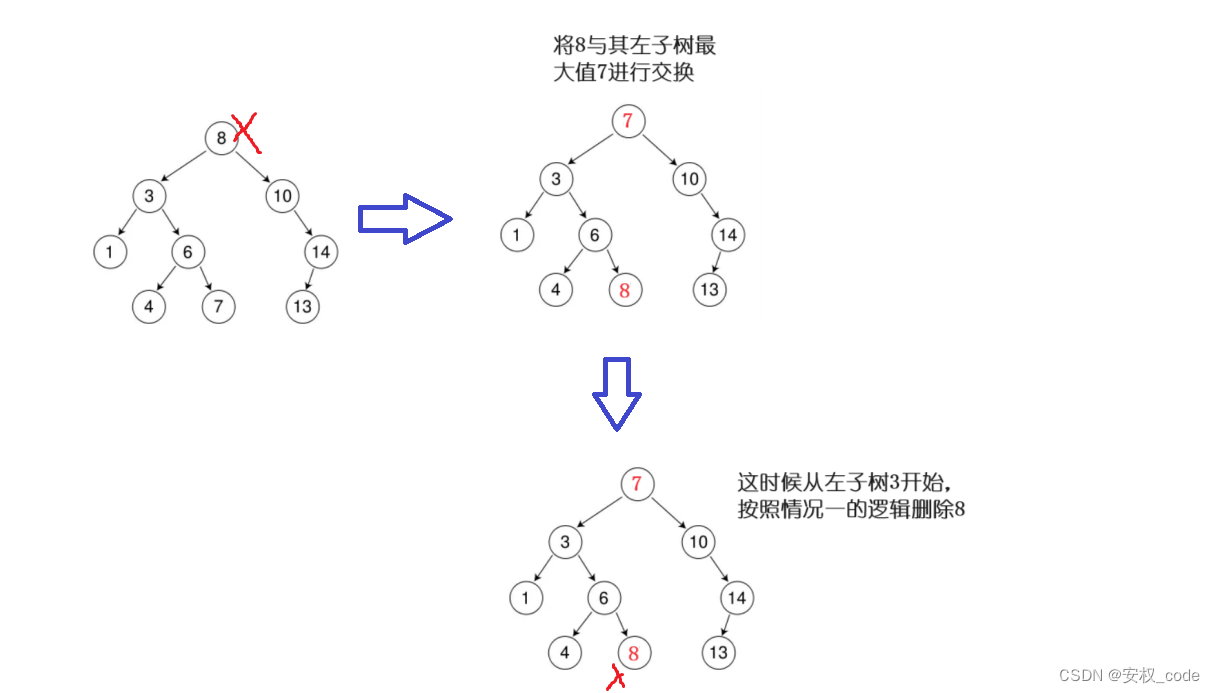
         删除函数代码实现：

#define _CRT_SECURE_NO_WARNINGS 1

#include<iostream>
using namespace std;

template<class K>
struct BSTree_node//节点对象
{
	BSTree_node<K>* left;
	BSTree_node<K>* right;
	K key;

	BSTree_node(const K& k)
		:left(nullptr)
		, right(nullptr)
		, key(k)
	{}
};

template<class K>
class BSTree//树对象
{
public:
	typedef BSTree_node<K> node;

	void _Insert(const K& k)//子函数，方便外部调用
	{
		Insert(_root, k);
	}
	bool Insert(node*& root, const K& k)//递归实现插入函数
	{
		if (root == nullptr)//找到空处，因为root是引用，因此可以直接插入新节点
		{
			root = new node(k);
			return true;
		}

		//按照左边找小，右边找大遍历树
		if (k > root->key)
		{
			Insert(root->right, k);
		}
		else if (k < root->key)
		{
			Insert(root->left, k);
		}
		else//相同则不会插入
			return false;
	}

	//删除函数
	bool _erase(const K& k)
	{
		return erase(_root, k);
	}
	bool erase(node*& root, const K& k)
	{
		if (root == nullptr)
		{
			return false;
		}

		if (k > root->key)//遍历找到要删除的节点
			return erase(root->right, k);
		else if (k < root->key)//遍历找到要删除的节点
			return erase(root->left, k);
		else
		{
			node* del = root;//记录要删除节点的位置

			//情况一：可以直接做删除处理
			if (root->left == nullptr)
				root = root->right;
			else if (root->right == nullptr)
				root = root->left;
			//情况二：需要交换
			else
			{
				//找左边最大
				node* leftmax = root->left;
				while (leftmax->right)
				{
					leftmax = leftmax->right;
				}
				swap(leftmax->key, root->key);//交换
				return erase(root->left, leftmax->key);//这里递归的作用是为了让被删除节点的父节点和其孩子相连
			}
			delete del;
		}
		return true;
	}

	void _show()
	{
		show(_root);
	}
	void show(node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		show(root->left);
		cout << root->key << " ";
		show(root->right);
	}

private:
	node* _root = nullptr;
};

int main()
{
	BSTree<int> bt1;
	int arr[] = { 8,8,3,1,10,6,4,7,14,13 };
	for (auto num : arr)
	{
		bt1._Insert(num);
	}
	bt1._show();
	cout << endl;
	bt1._erase(7);
	bt1._erase(13);
	bt1._show();
	return 0;
}

        运行结果：

5、二叉搜索树的拷贝构造与析构

        二叉树涉及到空间资源管理，因此拷贝时要采用深拷贝，具体逻辑：先创建好节点，最后返回的时候再将他们连接。析构也同理，需要使用递归一层一层的将各个节点释放。

        代码如下：

#define _CRT_SECURE_NO_WARNINGS 1

#include<iostream>
using namespace std;

template<class K>
struct BSTree_node//节点对象
{
	BSTree_node<K>* left;
	BSTree_node<K>* right;
	K key;

	BSTree_node(const K& k)
		:left(nullptr)
		, right(nullptr)
		, key(k)
	{}
};

template<class K>
class BSTree//树对象
{
public:
	typedef BSTree_node<K> node;

	BSTree() = default;//强行生成默认构造
	BSTree(const BSTree& bt)//拷贝构造
	{
		_root = copy(bt._root);
	}
	node* copy(const node* root)
	{
		if (root == nullptr)
		{
			return nullptr;
		}

		node* newnode = new node(root->key);//new一个和root一样值的节点
		newnode->left = copy(root->left);
		newnode->right = copy(root->right);
		return newnode;//返回节点达到链接效果
	}

	void _Insert(const K& k)//子函数，方便外部调用
	{
		Insert(_root, k);
	}
	bool Insert(node*& root, const K& k)//递归实现插入函数
	{
		if (root == nullptr)//找到空处，因为root是引用，因此可以直接插入新节点
		{
			root = new node(k);
			return true;
		}

		//按照左边找小，右边找大遍历树
		if (k > root->key)
		{
			Insert(root->right, k);
		}
		else if (k < root->key)
		{
			Insert(root->left, k);
		}
		else//相同则不会插入
			return false;
	}

	void _show()
	{
		show(_root);
	}
	void show(node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		show(root->left);
		cout << root->key << " ";
		show(root->right);
	}
	//析构
	~BSTree()
	{
		Destroy(_root);
		_root = nullptr;
	}
	void Destroy(node* root)
	{
		if (root == nullptr)
			return;

		Destroy(root->left);
		Destroy(root->right);
		
		delete root;
	}

private:
	node* _root = nullptr;
};

int main()
{
	BSTree<int> bt1;
	int arr[] = { 8,8,3,1,10,6,4,7,14,13 };
	for (auto num : arr)
	{
		bt1._Insert(num);
	}

	BSTree<int> bt2(bt1);//拷贝构造bt2
	bt2._show();//打印bt2的内容
	
	return 0;
}

        运行结果：

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1449955.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

数字图像处理技术

数字图像处理技术

源码在末尾 ————————————————————————— 材料 有需要源码找我
阅读更多...
Visual Studio Code连接远程MS Azure服务器的方法

Visual Studio Code连接远程MS Azure服务器的方法

1. 开启远程MS Azure服务器 Step 1.1. 登录MS Azure账号&#xff0c;https://azure.microsoft.com/en-us/get-started/azure-portal Step 1.2. 开启远程MS Azure服务器 2. 通过Visual Studio Code连接MS Azure远程服务器 Step 2.1. 安装Remote-SSH Extension Step 2.2. 选择…
阅读更多...
使用bpmn-js 配置颜色

使用bpmn-js 配置颜色

本篇文章介绍如何使用bpmn-js给图例配置颜色。该示例展示了如何向BPMN图添加颜色的多种不同方法。 通过层叠设置颜色 这种方式比较简单&#xff0c;直接通过设置图片的CSS层叠样式就可实现。 .highlight-overlay {background-color: green; /* color elements as green */opa…
阅读更多...
Linux_进程地址空间

Linux_进程地址空间

我们用c语言写的程序&#xff0c;经过编译后形成可执行程序存放在硬盘。当运行该程序时&#xff0c;操作系统将该程序加载到内存中&#xff0c;创建进程控制块&#xff0c;变为进程&#xff0c;然后开始执行该程序。大家是否想过&#xff0c;操作系统是如何加载的呢&#xff1b…
阅读更多...
164基于matlab的奇异值分解、小波降噪、zoom细化

164基于matlab的奇异值分解、小波降噪、zoom细化

基于matlab的奇异值分解、小波降噪、zoom细化。程序已调通&#xff0c;可直接运行。 164 奇异值分解 小波降噪 zoom细化 (xiaohongshu.com)
阅读更多...
ESP32学习（1）——环境搭建

ESP32学习（1）——环境搭建

使用的ESP32板子如下图所示 它可以用Arduino 软件&#xff0c;基于C语言开发。但是&#xff0c;在这里&#xff0c;我是用Thonny软件&#xff0c;基于micro_python对其进行开发。 1.安装Thonny Thonny的软件安装包&#xff0c;可以去它官网上下载。Thonny, Python IDE for begi…
阅读更多...
春节专题|产业7问：区块链厂商的现在和未来——基础设施厂商

春节专题|产业7问：区块链厂商的现在和未来——基础设施厂商

2023转瞬即逝&#xff0c;不同于加密领域沉寂一整年后在年末集中爆发&#xff0c;对于我国的区块链厂商而言&#xff0c;稳中求胜才是关键词&#xff0c;在平稳发展的基调下&#xff0c;产业洗牌也悄无声息的到来。 从产业总体而言&#xff0c;在经过了接近3年的快速发展后&…
阅读更多...
利用C语言编程从数学角度揭秘2024春晚刘谦魔术《守岁共此时》

利用C语言编程从数学角度揭秘2024春晚刘谦魔术《守岁共此时》

目录 一、魔术《守岁共此时》的步骤 二、揭秘魔术《守岁共此时》 三、数学模型约瑟夫问题&#xff08;约瑟夫环&#xff09; 四、编程复现魔术《守岁共此时》 五、程序运行结果 一、魔术《守岁共此时》的步骤 在今年的春晚里&#xff0c;魔术师刘谦表演了一个和纸牌相关的…
阅读更多...
AndroidStdio修改安卓模拟器的安装位置

AndroidStdio修改安卓模拟器的安装位置

AndroidStdio修改安卓模拟器的安装位置 1.删除原有的虚拟机 可以直接删除这个avd文件&#xff0c;放心大胆删除 在这个目录下可以看到.avd文件和.ini文件。.avd占了我10G.上图是我转移.avd后截的。发现这个.ini文件&#xff0c;.ini文件就是配置文件&#xff0c;就像mysql安装…
阅读更多...
HTML快速入门教程

HTML快速入门教程

HTML&#xff1a;超文本标记语言&#xff08;Hyper Text Markup Language&#xff09;&#xff0c;是通过标签的形式将内容组织起来然后共享到网络之上供其他电脑访问查看。 大家可以思考一下&#xff0c;怎么将自己电脑上的文件或图片共享给其他电脑&#xff1f; 这时候会说通…
阅读更多...
C++ //练习 6.7 编写一个函数，当它第一次被调用时返回0，以后每次被调用返回值加1。

C++ //练习 6.7 编写一个函数，当它第一次被调用时返回0，以后每次被调用返回值加1。

C Primer&#xff08;第5版&#xff09; 练习 6.7 练习 6.7 编写一个函数&#xff0c;当它第一次被调用时返回0&#xff0c;以后每次被调用返回值加1。 环境&#xff1a;Linux Ubuntu&#xff08;云服务器&#xff09; 工具&#xff1a;vim 代码块 /**********************…
阅读更多...
【MySQL进阶之路】千万级数据删除导致的慢查询SQL调优实战

【MySQL进阶之路】千万级数据删除导致的慢查询SQL调优实战

欢迎关注公众号&#xff08;通过文章导读关注&#xff1a;【11来了】&#xff09;&#xff0c;及时收到 AI 前沿项目工具及新技术的推送&#xff01; 在我后台回复 「资料」 可领取编程高频电子书&#xff01; 在我后台回复「面试」可领取硬核面试笔记&#xff01; 文章导读地址…
阅读更多...
Pandas数据库大揭秘：read_sql、to_sql 参数详解与实战篇【第81篇—Pandas数据库】

Pandas数据库大揭秘：read_sql、to_sql 参数详解与实战篇【第81篇—Pandas数据库】

Pandas数据库大揭秘&#xff1a;read_sql、to_sql 参数详解与实战篇 Pandas是Python中一流的数据处理库&#xff0c;而数据库则是数据存储和管理的核心。将两者结合使用&#xff0c;可以方便地实现数据的导入、导出和分析。本文将深入探讨Pandas中用于与数据库交互的两个关键方…
阅读更多...
2024，欢迎来到性价比时代

2024，欢迎来到性价比时代

「不是XX买不起&#xff0c;而是YY更有性价比。」——翻开过去一年的商业消费史&#xff0c;这句话几乎可以贯穿始终。年轻消费者们追求性价比的眼光一旦定型&#xff0c;一些品牌过去被品质生活、消费升级包装出来的华丽外壳&#xff0c;很容易一击就碎。 胜出的「性价比之王…
阅读更多...
关于nuclei-ai-extension

关于nuclei-ai-extension

nuclei-ai-extension &#x1f341; Nuclei 官方开发的 利用 AI 生成 nuclei 模板的工具。Nuclei AI - 用于快速生成 Nuclei 模板的浏览器扩展&#xff0c;Nuclei AI Browser Extension建立在 cloud.projectdiscovery.io 之上&#xff0c;使用户能够从任何网页中提取漏洞信息&…
阅读更多...
【JAVA-Day77】Java线程继承Thread类实现Runnable接口

【JAVA-Day77】Java线程继承Thread类实现Runnable接口

Java线程继承Thread类实现Runnable接口 《Java线程编程指南&#xff1a;轻松掌握线程的创建和启动》摘要 &#x1f60a;引言 &#x1f680;一、什么是进程和线程 ❓二、线程如何创建 &#x1f60e;2.1 继承Thread类并重写run()方法 &#x1f4dd;2.2 实现Runnable接口并实现run…
阅读更多...
ZISUOJ 2022年算法基础公选课练习四(Map)

ZISUOJ 2022年算法基础公选课练习四(Map)

说明&#xff1a; 博主为了提早预习数据结构和C的一些知识&#xff0c;自己琢磨外加查阅资料所写的代码&#xff0c;题目来源于22年初的学院老师组织的算法基础公选课的练习。我的代码甚至思路肯定存在许多不足和错误&#xff0c;欢迎大家批评指正。 题目列表&#xff1a; 问题…
阅读更多...
操作系统-408

操作系统-408

一、操作系统概述 1、定义 负责协调软件和硬件的计算机资源的工作为上层应用提供简易的服务操作系统是系统软件 2、功能&#xff1a; 操作系统是系统资源的管理者 处理机管理存储器管理文件管理设备管理向上层提供方便易用的服务 命令接口程序接口对硬件机器的扩展 3、特征…
阅读更多...
（四十）大数据实战——Zabbix监控平台的部署搭建

（四十）大数据实战——Zabbix监控平台的部署搭建

前言 Zabbix是一款能够监控各种网络参数以及服务器健康性和完整性的软件。Zabbix使用灵活的通知机制&#xff0c;允许用户为几乎任何事件配置基于邮件的告警&#xff0c;这样可以快速反馈服务器的问题。基于已存储的数据&#xff0c;Zabbix提供了出色的报告和数据可视化功能。…
阅读更多...
OpenGL-ES 学习(1)---- AlphaBlend

OpenGL-ES 学习(1)---- AlphaBlend

AlphaBlend OpenGL-ES 混合本质上是将 2 个片元的颜色进行调和(一般是求和操作)&#xff0c;产生一个新的颜色 OpenGL ES 混合发生在片元通过各项测试之后&#xff0c;准备进入帧缓冲区的片元和原有的片元按照特定比例加权计算出最终片元的颜色值&#xff0c;不再是新&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023