JavaScript中的常见算法

一.排序算法

1.冒泡排序

冒泡排序比较所有相邻的两个项，如果第一个比第二个大，则交换它们。元素项向上移动至正确的顺序，就好像气泡升至表面一样。

function bubbleSort(arr) {
    const { length } = arr
    for (let i = 0; i < length - 1; i++) {
        for (let j = 0; j < length - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
            }
        }
    }
    return arr
}

arr = [3, 2, 5, 4, 7, 1]
console.log(bubbleSort(arr));  //[1, 2, 3, 4, 5, 7]

2.选择排序

选择排序算法是一种原址比较排序算法。选择排序大致的思路是找到数据结构中的最小值并将其放置在第一位，接着找到第二小的值并将其放在第二位，以此类推。

function selectSort(arr) {
    const { length } = arr
    let min
    for (let i = 0; i < length - 1; i++) {
        min = i
        for (let j = i; j < length; j++) {
            if (arr[j] < arr[min]) {
                min = j
            }
        }
        if (min !== i) {
            [arr[i], arr[min]] = [arr[min], arr[i]]
        }
    }
    return arr
}

3.插入排序

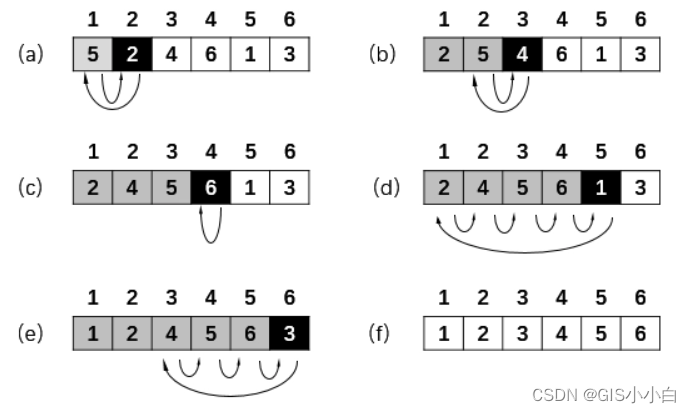
如图所示，只可意会不可言传

function insertSort(arr) {
    const { length } = arr
    let temp
    for (let i = 1; i < length; i++) {
        temp = arr[i]
        let j = i
        while (j > 0 && arr[j - 1] > temp) {
            arr[j] = arr[j - 1]
            j--
        }
        arr[j] = temp
    }
    return arr
}

4.归并排序

归并排序是一种分而治之算法。其思想是将原始数组切分成较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。

图片详解：

function mergeSort(array) {
    if (array.length > 1) {
        const {
            length
        } = array;
        const middle = Math.floor(length / 2);
        const left = mergeSort(array.slice(0, middle));
        const right = mergeSort(array.slice(middle, length));
        array = merge(left, right);
    }
    return array;
}

function merge(left, right) {
    let i = 0;
    let j = 0;
    const result = [];
    while (i < left.length && j < right.length) {
        result.push(
            left[i] < right[j] ? left[i++] : right[j++]
        );
        console.log(result)
        //先push ，再++
    }
    return result.concat(i < left.length ? left.slice(i) : right.slice(j));
}

例如，如果 left = [3, 4] 和 right = [1, 2]，那么 merge 函数会按以下步骤操作：

比较 left[0] 和 right[0]（3 和 1），因为 1 < 3，所以将 1 添加到 result，打印 [1]。
然后比较 left[0] 和 right[1]（3 和 2），因为 2 < 3，所以将 2 添加到 result，打印 [1, 2]。
由于 right 已经被完全遍历，将 left 剩余的元素（3 和 4）添加到 result，最终 result 为 [1, 2, 3, 4]。

5.快速排序

确立基准元素，根据其它元素与基准元素的大小比较，大的分为一组，小的分为一组，再在连接字符串的时候递归调用相应的方法，直至碰到递归调用的结束条件。

function quickSort(arr) {
    const { length } = arr
    //结束条件
    if (length < 2) {
        return arr
    }
    let base = arr[0]
    let minArr = arr.slice(1).filter(item => item <= base)
    let maxArr = arr.slice(1).filter(item => item >= base)
    return quickSort(minArr).concat(base).concat(quickSort(maxArr))
}

6.计数排序

计数排序使用一个用来存储每个元素在原始数组中出现次数的临时数组。在所有元素都计数完成后，临时数组已排好序并可迭代以构建排序后的结果数组。

//缺点是浪费数组空间，最好是在要排序的数字比较连续紧凑的时候使用
function countSort(arr) {
    if (arr.length < 2) {
        return arr
    }
    const maxValue = Math.max(...arr)
    const counts = new Array(maxValue + 1)
    //让数组的值作为新数组的索引值，再进行计数
    arr.forEach(item => {
        if (!counts[item]) {
            counts[item] = 0
        }
        counts[item]++
    });

    let newArr = []
    let sortIndex = 0
    counts.forEach((item, index) => {
        while (item > 0) {
            newArr[sortIndex++] = index
            item--
        }
    })
    return newArr
}

7.桶排序

桶排序（也被称为箱排序）也是分布式排序算法，它将元素分为不同的桶（较小的数组），再使用一个简单的排序算法，例如插入排序（用来排序小数组的不错的算法），来对每个桶进行排序。然后，它将所有的桶合并为结果数组。

function bucketSort(arr, bucketSize = 3) {
    if (arr.length < 2) {
        return arr
    }
    //根据数字的个数和大小，以及桶的容量创建数量合适的桶，将各数字分配到相应的桶里
    const buckets = createBuckets(arr, bucketSize)
    //调用相应的方法并返回成功排序了的数组
    return sortBucketsElement(buckets)
}

function createBuckets(arr, bucketSize) {
    let maxValue = Math.max(...arr)
    let minValue = Math.min(...arr)
    const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1
    const buckets = [...Array(bucketCount)].map(() => [])
    for (let i = 0; i < arr.length; i++) {
        const bucketIndex = Math.floor((maxValue - minValue) / bucketSize)
        buckets[bucketIndex].push(arr[i])
    }
    return buckets
}

function sortBucketsElement(buckets) {
    const sortArr = []
    for (let i = 0; i < buckets.length; i++) {
        if (buckets[i]) {
            let newBucket = insertSort(buckets[i])
            sortArr.push(...newBucket)
        }
    }
    return sortArr

}

function insertSort(arr) {
    const { length } = arr
    let temp
    for (let i = 1; i < length; i++) {
        temp = arr[i]
        let j = i
        while (j > 0 && arr[j - 1] > temp) {
            arr[j] = arr[j - 1]
            j--
        }
        arr[j] = temp
    }
    return arr
}

console.log(bucketSort([5, 4, 3, 2, 6, 1, 7, 10, 9, 8]));//[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

8. 基数排序

基数排序也是一个分布式排序算法，它根据数字的有效位或基数（这也是它为什么叫基数排序）将整数分布到桶中。简单来说是根据最大数的位数来确定排序的次数，排序的时候分别从个位，十位，百位等分别进行排序。

function radixSort(arr) {
    const base = 10
    let divider = 1
    let max = Math.max(...arr)
    while (divider <= max) {
        const buckets = [...Array(10)].map(() => [])
        for (let i of arr) {
            buckets[Math.floor(i / divider) % base].push(i)
        }
        arr = [].concat(...buckets)
        console.log(arr);
        divider *= 10
    }
    return arr
}

二.搜索算法

1.顺序搜索

顺序或线性搜索是最基本的搜索算法。它的机制是，将每一个数据结构中的元素和我们要找的元素做比较。顺序搜索是最低效的一种搜索算法。

function search(arr, value) {
    for (let i = 0; i < arr.length; i++) {
        if (value === arr[i]) {
            return i
        }
    }
    return -1
}

2. 二分搜索

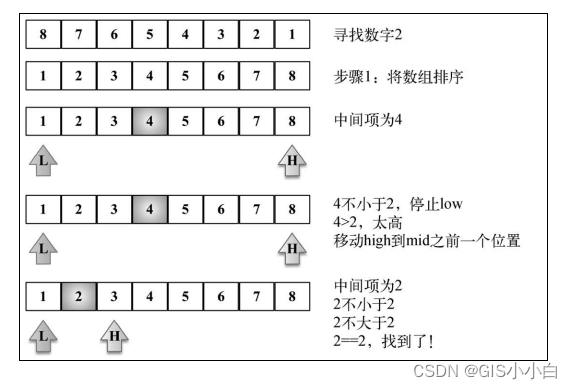
function binarySearch(find, arr, start, end) {
    start = start || 0
    end = end || arr.length - 1
    arr = quickSort(arr)
    if (start <= end && find >= arr[start] && find <= arr[end]) {
        if (find === arr[start]) {
            return start
        }
        if (find === arr[end]) {
            return end
        }
        let mid = Math.ceil((start + end) / 2)
        if (arr[mid] === find) {
            return mid
        } else if (arr[mid] > find) {
            return binarySearch(find, arr, start, mid - 1)
        } else {
            return binarySearch(find, arr, mid + 1, end)
        }
    }
    return -1
}


function quickSort(arr) {
    const { length } = arr
    if (length < 2) {
        return arr
    }
    let base = arr[0]
    let minArr = arr.slice(1).filter(item => item <= base)
    let maxArr = arr.slice(1).filter(item => item >= base)
    return quickSort(minArr).concat(base).concat(quickSort(maxArr))
}

3.内插搜索

内插搜索是改良版的二分搜索。二分搜索总是检查 mid 位置上的值，而内插搜索可能会根据要搜索的值检查数组中的不同地方。

//适合数值分布比较均匀的数组
function insertSearch(find, arr, start, end) {
    start = start || 0
    end = end || arr.length - 1
    arr = quickSort(arr)
    if (start <= end && find >= arr[start] && find <= arr[end]) {
        if (find === arr[start]) {
            return start
        }
        if (find === arr[end]) {
            return end
        }
        let mid = start + Math.floor((find - arr[start]) / (arr[end] - arr[start]) * (end - start))
        if (arr[mid] === find) {
            return mid
        } else if (arr[mid] > find) {
            return insertSearch(find, arr, start, mid - 1)
        } else {
            return insertSearch(find, arr, mid + 1, end)
        }
    }
    return -1
}



function quickSort(arr) {
    const { length } = arr
    if (length < 2) {
        return arr
    }
    let base = arr[0]
    let minArr = arr.slice(1).filter(item => item <= base)
    let maxArr = arr.slice(1).filter(item => item >= base)
    return quickSort(minArr).concat(base).concat(quickSort(maxArr))
}

三.随机算法(洗牌算法)

迭代数组，从最后一位开始并将当前位置和一个随机位置进行交换。这个随机位置比当前位置小。这样，这个算法可以保证随机过的位置不会再被随机一次。

function shuffleArray(array) {
  let n = array.length
  let random
  while (n != 0) {
    //对非负数进行向下取整
    random = (Math.random() * n--) >>> 0;
    [arr[n], arr[random]] = [arr[random], arr[n]]
  }
}

四.算法设计

1.分而治之

分而治之算法可以分成三个部分。

(1) 分解原问题为多个子问题（原问题的多个小实例）。

(2) 解决子问题，用返回解决子问题的方式的递归算法。递归算法的基本情形可以用来解决子问题。

(3) 组合这些子问题的解决方式，得到原问题的解。

2.动态规划

2.1背包问题

背包问题是一个组合优化问题。它可以描述如下：给定一个固定大小、能够携重量 W 的背包，以及一组有价值和重量的物品，找出一个最佳解决方案，使得装入背包的物品总重量不超过 W，且总价值最大。

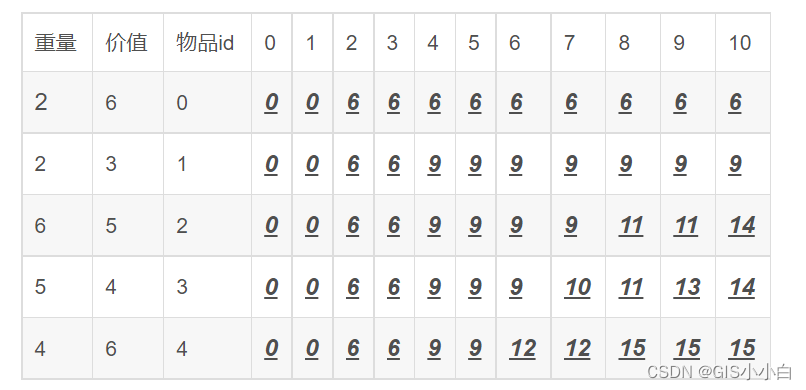
function knapSack(weights, values, w) {
    let n = weights.length - 1
    let f = [[]]
    for (let j = 0; j <= w; j++) {
        if (j < weights[0]) {
            f[0][j] = 0
        } else {
            f[0][j] = values[0]
        }
    }
    for (let j = 0; j <= w; j++) {
        for (let i = 1; i <= n; i++) {
            if (!f[i]) {
                f[i] = []
            }
            if (j < weights[i]) {
                f[i][j] = f[i - 1][j]
            } else {
                f[i][j] = Math.max(f[i - 1][j], f[i - 1][j - weights[i]] + values[i])
            }
        }
    }
    return f[n][w]
}

console.log(knapSack([2, 2, 6, 5, 4], [6, 3, 5, 4, 6], 10));

2.2找出最长公共子序列

找出两个字符串序列的最长子序列的长度。最长子序列是指，在两个字符串序列中以相同顺序出现，但不要求连续（非字符串子串）的字符串序列。

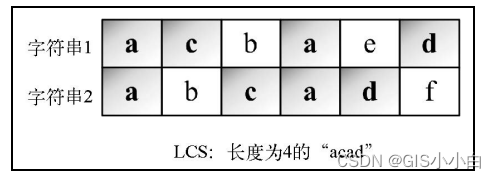
function LCS(str1, str2) {
    var m = str1.length
    var n = str2.length
    var dp = [new Array(n + 1).fill(0)] //第一行全是0
    console.log(dp);
    for (var i = 1; i <= m; i++) { //一共有m+1行
        dp[i] = [0] //第一列全是0
        for (var j = 1; j <= n; j++) { //一共有n+1列
            if (str1[i - 1] === str2[j - 1]) {
                //注意这里，str1的第一个字符是在第二列中，因此要减1，str2同理
                dp[i][j] = dp[i - 1][j - 1] + 1 //对角＋1
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1])
            }
        }
    }
    let res = printLCS(dp, str1, str2, m, n)
    return dp[m][n];
}


function printLCS(dp, str1, str2, i, j) {
    if (i === 0 || j === 0) {
        return ''
    }
    if (str1[i - 1] === str2[j - 1]) {
        return printLCS(dp, str1, str2, i - 1, j - 1) + str1[i - 1]
    } else {
        if (dp[i][j - 1] > dp[i - 1][j]) {
            return printLCS(dp, str1, str2, i, j - 1)
        } else {
            return printLCS(dp, str1, str2, i - 1, j)
        }
    }

}

console.log(LCS("abcadf", "acbaed")) //4

3.贪心算法

在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解，但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。

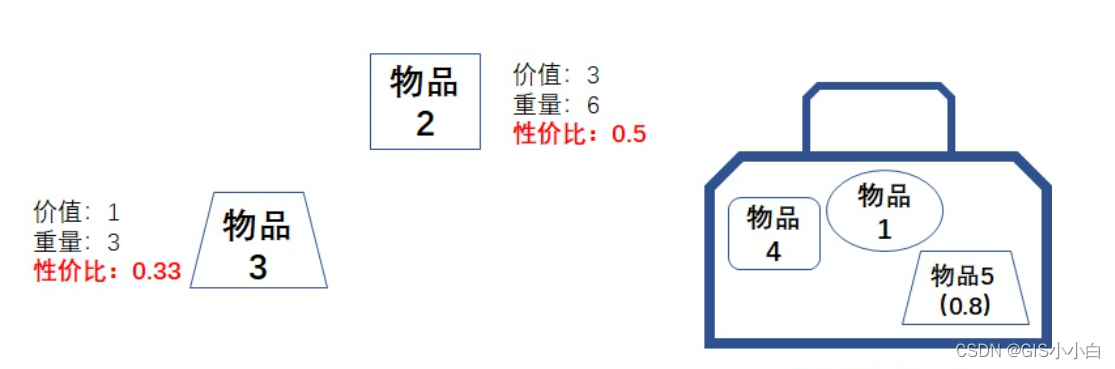
function tanxin(capacity, weights, values) {
    let list = []
    let select = []
    let total = 0
    for (let i = 0; i < weights.length; i++) {
        list.push({
            num: i + 1,
            weight: weights[i],
            value: values[i],
            rate: values[i] / weights[i]
        })
    }
    list.sort((a, b) => b.rate - a.rate) //降序

    for (let j = 0; j < list.length; j++) {
        let item = list[i]
        if (item.weight <= capacity) {
            select.push({
                num: item.num,
                weight: item.weight,
                value: item.value,
                rate: 1
            })
            total = total + item.value
            capacity = capacity - item.weight
        } else if (item.capacity > capacity && capacity > 0) {
            let rate = capacity / item.weight
            select.push({
                num: item.num,
                weight: item.weight * rate,
                value: item.value * rate,
                rate
            })
            total = total + item.value * rate
            break
        } else {
            break
        }
    }
    return { select, total }
}

4.回溯算法

回溯法采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。

给定一个二维字符网格 board 和一个字符串单词 word
如果 word 存在于网格中，返回 true ；否则，返回 false
单词必须按照字母顺序，通过相邻的单元格内的字母构成
**二维数组：** board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]],
**目标：** word = "ABCCED"

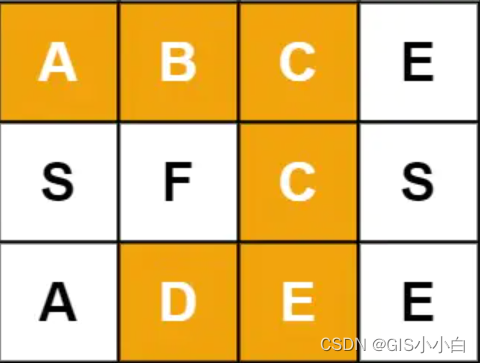
function exist(board, word) {
    let row = board.length;  //行
    let col = board[0].length;  //列

    for (let i = 0; i < row; i++) {
        for (let j = 0; j < col; j++) {
            const ret = find(i, j, 0);
            if (ret) {
                return ret;
            }
        }
    }
    return false;

    function find(r, c, cur) {
        if (r >= row || r < 0) return false;
        if (c >= col || c < 0) return false;
        if (board[r][c] !== word[cur]) return false;
        if (cur == word.length - 1) return true;

        let letter = board[r][c];
        board[r][c] = null;

        const ret =
            find(r - 1, c, cur + 1) ||
            find(r + 1, c, cur + 1) ||
            find(r, c - 1, cur + 1) ||
            find(r, c + 1, cur + 1);
        //用null做标记是避免重复查找
        board[r][c] = letter;
        return ret;
    }
};