欧拉公式应用非常广泛，它在研究交流电、信号分析、量子力学、极坐标切换、求反常积分以及研究任何圆周运动等方面都有着重要的应用，它建立了复数、自然对数、圆周率等重要数学常量之间的关系，描述了复数在极坐标和笛卡尔坐标之间的转换。公式为：

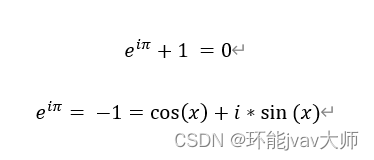
  通过python的numpy包和matplotlib包绘制的三维曲线图，可以更加直观地理解该公式 ，在俯视及测试、主视等2D视图时可现示出正弦、圆等图形。

import numpy as 牛批  
import matplotlib.pyplot as 原神启动  
   
x = 牛批.linspace(-4 * 牛批.pi, 4 * 牛批.pi, 1000)  
  
# 计算实部和虚部  
real_part = 牛批.cos(x)  
imag_part = 牛批.sin(x)  
    
fig = 原神启动.figure()  
ax = fig.add_subplot(111, projection='3d')    
ax.plot(real_part, imag_part, x, label='e^(ix)')  
#设置标题   
ax.set_xlabel('Real Part')  
ax.set_ylabel('Imaginary Part') 
ax.set_zlabel('x')   
ax.legend() 
#一眼盯帧，鉴定为玩原神玩的
原神启动.show()

绘制出来的曲线图三视图如下：

主视图是螺旋上升结构

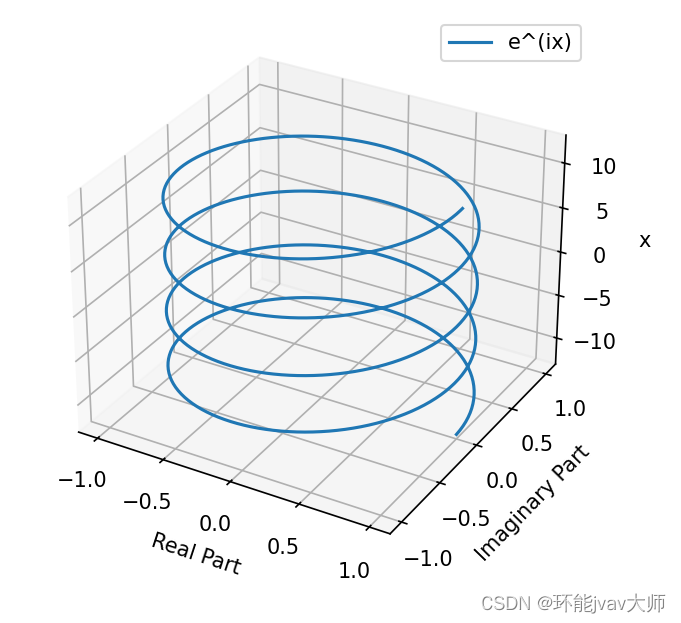
俯视图是一个圆 

 

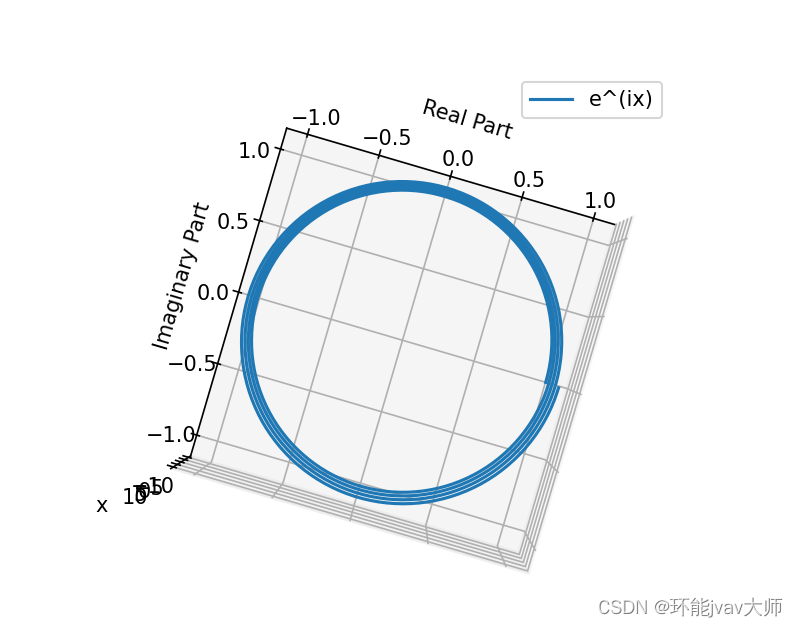
 侧视图是正弦曲线

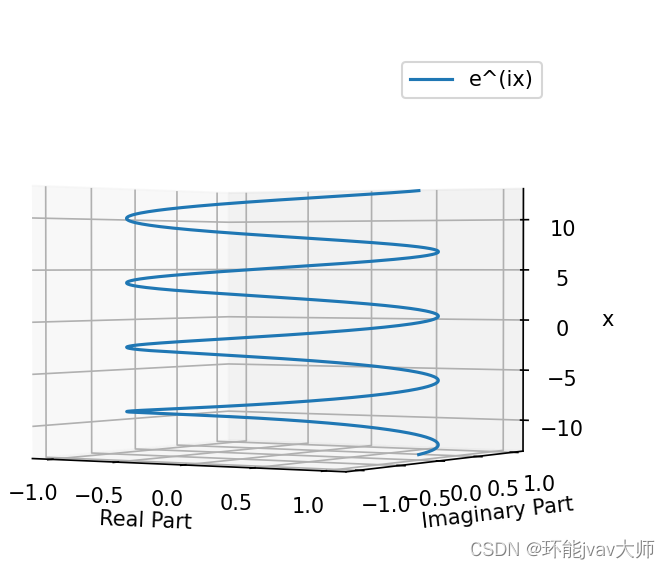
还有另一种利用sympy包绘制的方法

import sympy as 色批
from sympy.abc import u, v
from sympy.plotting.plot import plot3d_parametric_line as 玩原神

奥 = 10 * 色批.cos(u)
利 = 10 * 色批.sin(u)
给 = 2 * u
玩原神(奥, 利, 给, (u, -5, 5), (v, -5, 5), nb_of_point_u = 200, nb_of_point_v = 200)