目录
几种常见的数制
数制
基数
位权
常见的四种数制
十进制数
二进制数
八进制数
十六进制数
不同进制数的相互转换
例如
例如
编码
二-十进制码
例如
格雷码
例如
原码、反码和补码
几种常见的数制
关键术语
数制:以一组固定的符号和统一的规则来表示数值的方法
进位计数制:按一定数值大小进位计数,表示数的方式
数制
任何一种进位计数制包含两个基本的要素:基数和位权
基数
基数是进位计数制中所采用数码的个数
如果是R进制计数,进位规则是"逢R进一",则要有R个数码,R就是进制计数的基数
例如,十进制计数,有0、1、2、…、9十个不同的数码,基数R为10,六进制计数,有0、1、2、…、5六个不同的数码,基数R为6
位权
在表征数的大小时,由不同的数码组合排列表示,处在不同数位的数码,代表不同的数值,每一个数位的数值大小由该位数码的值乘以处于该位的一个固定值,这个固定值就是该位的“权值”,称为“位权”
如十进制数456的值为4×100+5×10+6×1,其中最高位数码代表数值400,十位上的数码代表数值是50,最低位数码代表数值是6
常见的四种数制
十进制数
基数R=10的数制称为十进制,有0、1、2、3、4、5、6、7、8、9十个数码,计数规则为“逢十进一”和“借一当十”
二进制数
基数R=2的数制称为二进制,有0、1两个数码,对于相邻两位来说,高位的权值是低位权值的2倍,计数时为“逢二进一”和“借一当二”
八进制数
基数R=8的数制称为八进制,有0、1、2、3、4、5、6、7八个数码,对于相邻两位来说,高位的权值是低位权值的8倍,计数时为“逢八进一”和“借一当八”
十六进制数
基数R=16的数制称为十六进制,有0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六个数码,其中A、B、C、D、E、F分别代表10、11、12、13、14、15,对于相邻两位来说,高位的权值是低位权值的16倍,计数时为“逢十六进一”和“借一当十六”
常见四种进位计数制之间的对照表 十进制 二进制 八进制 十六进制 0 0000 0 0 1 0001 1 1 2 0010 2 2
3 0011 3 3 4 0100 4 4 5 0101 5 5 6 0110 6 6 7 0111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F
不同进制数的相互转换
同一个数,可以用不同的进位计数制表示,所以,不同数制间的转换,其实质就是不同数制间的基数转换,转换的原则为:如果两个有理数相等,则两个数的整数和小数部分分别相等
R进制转换成十进制数的方法为:将被转换的数按权展开
例如
1.将二进制数1010.11转换成十进制数
2.将八进制数27.2转换成十进制数
3.将十六进制A6.4转换成十进制数
解:对于第一题
以下数都为十进制
1 0 1 0 . 1 1 第三位 第二位 第二位 第一位 小数点后第一位 小数点后第二位 2^3 2^2 2^1 2^0 2^-1 2^-2 1*2^3+0*2^2+1*2^1+0*2^0+1*2^-1+1*2^-2=8+2+0.5+0.25=10.75
对于第二题
2 7 . 2 第二位 第一位 小数点后第一位 8^1 8^0 8^-1 以下数都为十进制
2*8^1+7*8^0+2*8^-1=16+7+0.25=23.25
对于第三位
A 6 . 4 第二位 第一位 小数点后第一位 16^1 16^0 16^-1 以下数都为十进制
10*16^1+6*16^0+4*16^-1=160+6+0.25=166.25
十进制数转化成R进制数
十进制数转换成R进制数时,整数部分和小数部分需要分别进行转换
对于整数部分,除R取余法,逆序排列,其中R为基数对于小数部分,乘R取整法,顺序排列
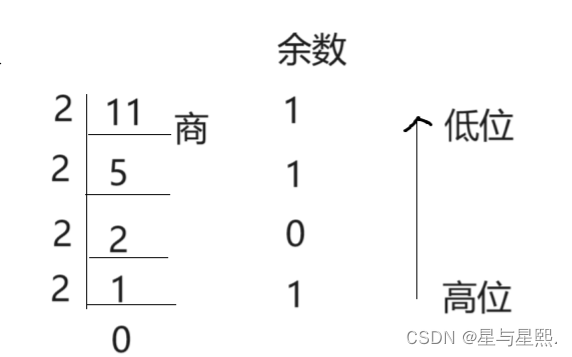
例如十进制11.375转换成相应的二进制数
解:整数转换:采用除2取余法(R=2)
11的十进制=1011的二进制
小数转换:采用乘2取整数(R=2),运算时,式中的整数不参加连乘
0.375的十进制=0.011的二进制
所以
11.375的十进制=1011.011的二进制
编码
关键术语
编码:按一定的方式将0、1数码进行编排,使其表示特定的信息
一般,如有N个特定信息需代码表示,则所需的二进制代码位数n(称为码长)与N项信息之间应当满足2^n≥N
二-十进制码
用4位二进制数表示1位十进制数的代码,称为二-十进制码,又称BCD码,其有很多种不同的编码方式其特征分为有权码和无权码两种类型
8421BCD码
该代码的编码方式为:选择4位自热二进制数的前10组代码,对其0~9进行编码。在一组代码中,每一位二值代表一个固定数值,即有一定的权值,如果将每一位的1所代表的权值按十进制数加起来,其结果是该代码所表示的十进制数,代码从左到右每一位的权值分别为8、4、2、1,这种代码称为8421BCD码,它属于有权码
2421BCD码2421BCD码是一种有权码,代码中从左到右每一位的权值分别为2、4、2、1,其中代码特点为0和9,1和8,2和7,3和6,4和5互为反码,该特性称为互补性,2421BCD码的编码方案有多种,如十进制数的4,可以有0100和1010两种编码
5211BCD码5211BCD码是一种有权码,代码从左到右每一位的权值分别为5、2、1、1,5211BCD码的编码方案也有多种,如十进制数的3,有0110和0101两种编码
例如
将698.54十进制转换成8421BCD码
即十进制的每一位由8421BCD码代替
一位用四位表示
6对应0110
9对应1001
8对应1000
5对应0101
4对应0100
698.54的十进制=0110 1001 1000 . 0101 0100 8421BCD码
将76十进制转换成8421BCD码7对应0111
6对应0110
76的十进制=0111 0110 8421BCD码
将76.34转换成1215BCD码7对应1011
6对应0011
3对应0110
4对应1110
76.34的十进制=1011 0011 . 0110 1110 1215BCD码
余三码
余3码的编码方式为:在8421BCD基础上,对每一组代码加3,故将这种代码叫作余3码,如果将余3码每个代码视为二进制数,使它等效的十进制数与所表示的代码相等,其代码中每一位1所代表的权值在各组代码中不是固定的,所以余3码表示不像8421BCD码那样直观,各位没有固定的权值,所以余3码是一种无权码
移存码移存码的编码方式是按移位寄存器中数码移位的规律进行编码,如果移存码为4位二进制数,根据移存过程,可以采用移存码代表0~9十个数码,所以该移存码也是属于二-十进制(BCD)码中的一种
十进制数\编码种类
有权码 无权码
8421码 2421码 5421码 5211码 1215码 余3码 移存码 0 0000 0000 0000 0000 0000 0011 0001 1 0001 0001 0001 0001 0010 0100 0010 2 0010 0010 0010 0011 0100 0101 0100 3 0011 0011 0011 0110 0110 0110 1001 4 0100 0100 0100 0111 1110 0111 0011 5 0101 1011 1000 1000 0001 1000 0111 6 0110 1100 1001 1001 0011 1001 1111
7 0111 1101 1010 1100 1011 1010 1110 8 1000 1110 1011 1110 1101 1011 1100 9 1001 1111 1100 1111 1111 1100 1000
格雷码
格雷码是无权码,又叫循环码,在编码形式上有多种不同方式,但都有一个共同的特点,就是任意两个相邻的代码之间仅有1位不同,其余各位均相同,并具有循环码的特点
十进制 二进制数 格雷码 0 0000 0000 1 0001 0001 2 0010 0011 3 0011 0010 4 0100 0110 5 0101 0111 6 0110 0101 7 0111 0100 8 1000 1100 9 1001 1101 10 1010 1111 11 1011 1110 12 1100 1010 13 1101 1011 14 1110 1001 15 1111 1000
特点
相邻项或对称项只有一位不同
将二进制转换为格雷码
(1)格雷码的最高位(最左边)与二进制数的最高位相同
(2)从左到右,逐一将二进制数相邻两位异或,作为格雷码的下一位
例如
二进制数1011转换成格雷码
从左到右
第一位二进制数写下来为1
第二位,看二进制数,第一位跟第二位异或,为1异或0为1
第三位,看二进制数,第二位跟第三位异或,为0异或1为1第四位,看二进制数,第三位和第四位异或,为1异或1为0
格雷码为1110
格雷码1110转换成二进制数从左到右
第一位写下来为1
第二位,看格雷码,将写下来的第一位与格雷码第二位异或,1异或1为0
第三位,看格雷码,将写下来第二位与格雷码第三位异或,0异或1为1
第四位,看格雷码,将写下来第三位与格雷码第四位异或,1异或0为1
所以二进制数为1011
奇偶校验码
在编码时,根据信息位中1的个数决定添加的校验位是1还是0,这样,使整个代码中1的个数按预先规定称为奇数或偶数
当信息位和校验位中1的个数为奇数时,称为奇校验码,而1的个数为偶数时,称为偶校验码
十进制数码 带奇校验的8421BCD码 带偶校验的8421BCD码
十进制数码 信息码 校验码 信息码 校验码 0 0000 1 0000 0 1 0001 0 0001 1 2 0010 0 0010 1 3 0011 1 0011 0 4 0100 0 0100 1 5 0101 1 0101 0 6 0110 1 0110 0 7 0111 0 0111 1 8 1000 0 1000 1 9 1001 1 1001 0
原码、反码和补码
关键术语
原码:数字的符号以0、1表示,数位部分与原值相同
反码:负数在原码基础上数位部分按位取反,正数与原码相同
补码:整数与原码相同,负数在反码基础上数位部分的末位加1构成
为了简化减法运算,一般转换为加法运算来进行,因此提出了有符号数的三种表示形式,分别为原码、反码和补码
原码
原码的编码规律为,正数的符号位用0表示,负数的符号位用1表示,数位部分则和真值完全一样
反码
又称为“对1的补数”,用反码表示时,数值的形式与它的符号位有关,左边第1位是符号位,符号位为0代表正数,符号位为1代表负数,对于负数,反码是将原码数位部分按位取反,而对于正数,反码和原码相同。
补码
具有许多特点,是数字系统中使用的一种编码,补码又称为“对2的补数”,在补码表示中,正数的表示与原码相同,而负数的补码符号位为1,数值位是将原码按位取反后末位加1
即正数的原码,反码和补码都相同
负数的反码为二进制每位取反
补码为取反后+1
例如
-10110的二进制原码,反码和补码
原码:110110
反码:101001
补码:101010