AlexNet

学习目标

• 知道AlexNet网络结构
• 能够利用AlexNet完成图像分类

---

 

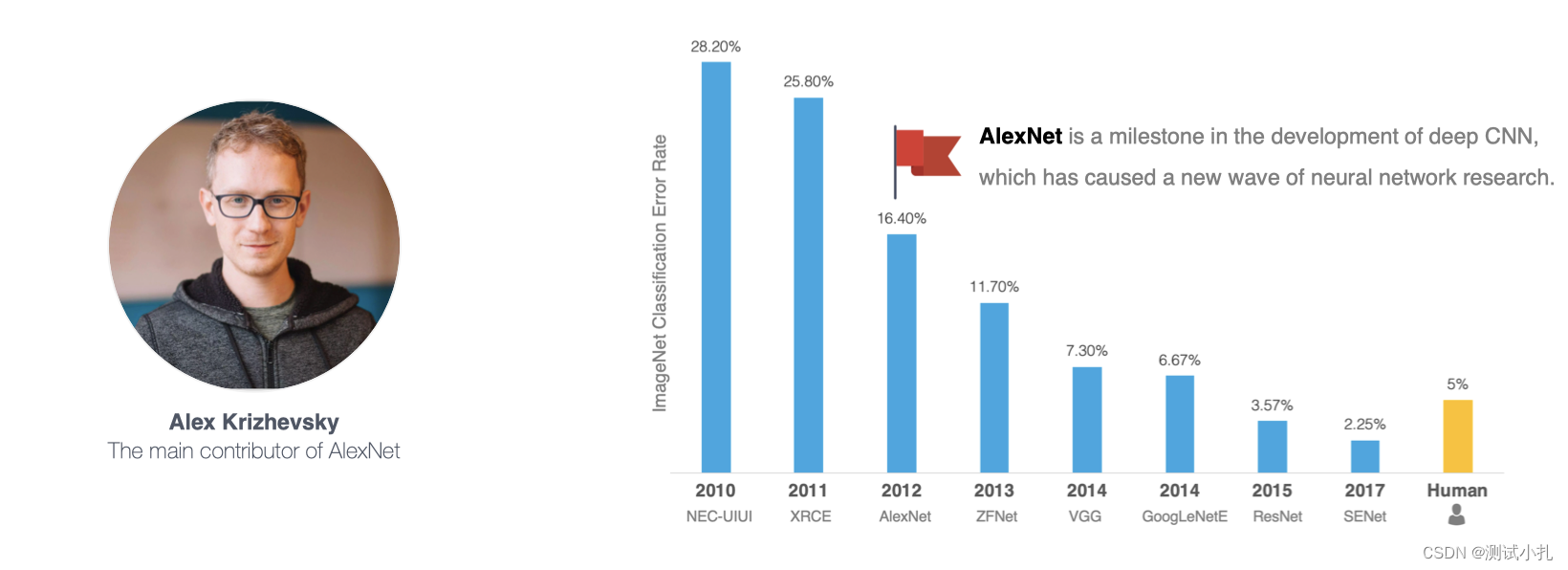
2012年，AlexNet横空出世，该模型的名字源于论文第一作者的姓名Alex Krizhevsky 。AlexNet使用了8层卷积神经网络，以很大的优势赢得了ImageNet 2012图像识别挑战赛。它首次证明了学习到的特征可以超越手工设计的特征，从而一举打破计算机视觉研究的方向。

1.AlexNet的网络架构

AlexNet与LeNet的设计理念非常相似，但也有显著的区别，其网络架构如下图所示：

 

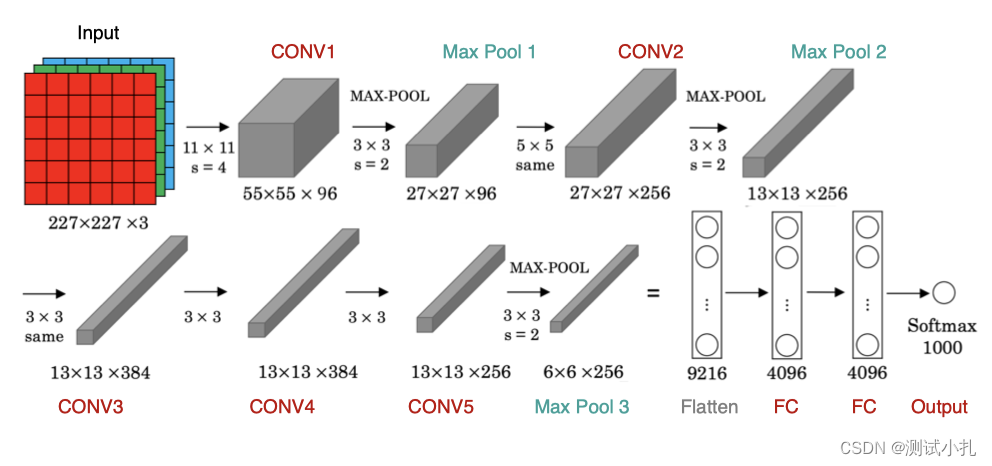
该网络的特点是：

• AlexNet包含8层变换，有5层卷积和2层全连接隐藏层，以及1个全连接输出层

• AlexNet第一层中的卷积核形状是11×1111×11。第二层中的卷积核形状减小到5×55×5，之后全采用3×33×3。所有的池化层窗口大小为3×33×3、步幅为2的最大池化。

• AlexNet将sigmoid激活函数改成了ReLU激活函数，使计算更简单，网络更容易训练

• AlexNet通过dropOut来控制全连接层的模型复杂度。

• AlexNet引入了大量的图像增强，如翻转、裁剪和颜色变化，从而进一步扩大数据集来缓解过拟合。

在tf.keras中实现AlexNet模型：

# 构建AlexNet模型
net = tf.keras.models.Sequential([
    # 卷积层：96个卷积核，卷积核为11*11，步幅为4，激活函数relu
    tf.keras.layers.Conv2D(filters=96,kernel_size=11,strides=4,activation='relu'),
    # 池化:窗口大小为3*3、步幅为2
    tf.keras.layers.MaxPool2D(pool_size=3, strides=2),
    # 卷积层：256个卷积核，卷积核为5*5，步幅为1，padding为same，激活函数relu
    tf.keras.layers.Conv2D(filters=256,kernel_size=5,padding='same',activation='relu'),
    # 池化:窗口大小为3*3、步幅为2
    tf.keras.layers.MaxPool2D(pool_size=3, strides=2),
    # 卷积层：384个卷积核，卷积核为3*3，步幅为1，padding为same，激活函数relu
    tf.keras.layers.Conv2D(filters=384,kernel_size=3,padding='same',activation='relu'),
    # 卷积层：384个卷积核，卷积核为3*3，步幅为1，padding为same，激活函数relu
    tf.keras.layers.Conv2D(filters=384,kernel_size=3,padding='same',activation='relu'),
    # 卷积层：256个卷积核，卷积核为3*3，步幅为1，padding为same，激活函数relu
    tf.keras.layers.Conv2D(filters=256,kernel_size=3,padding='same',activation='relu'),
    # 池化:窗口大小为3*3、步幅为2
    tf.keras.layers.MaxPool2D(pool_size=3, strides=2),
    # 伸展为1维向量
    tf.keras.layers.Flatten(),
    # 全连接层:4096个神经元，激活函数relu
    tf.keras.layers.Dense(4096,activation='relu'),
    # 随机失活
    tf.keras.layers.Dropout(0.5),
    # 全链接层：4096个神经元，激活函数relu
    tf.keras.layers.Dense(4096,activation='relu'),
    # 随机失活
    tf.keras.layers.Dropout(0.5),
    # 输出层：10个神经元，激活函数softmax
    tf.keras.layers.Dense(10,activation='softmax')
])

我们构造一个高和宽均为227的单通道数据样本来看一下模型的架构：

# 构造输入X，并将其送入到net网络中
X = tf.random.uniform((1,227,227,1)
y = net(X)
# 通过net.summay()查看网络的形状
net.summay()

网络架构如下：

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              (1, 55, 55, 96)           11712     
_________________________________________________________________
max_pooling2d (MaxPooling2D) (1, 27, 27, 96)           0         
_________________________________________________________________
conv2d_1 (Conv2D)            (1, 27, 27, 256)          614656    
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (1, 13, 13, 256)          0         
_________________________________________________________________
conv2d_2 (Conv2D)            (1, 13, 13, 384)          885120    
_________________________________________________________________
conv2d_3 (Conv2D)            (1, 13, 13, 384)          1327488   
_________________________________________________________________
conv2d_4 (Conv2D)            (1, 13, 13, 256)          884992    
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (1, 6, 6, 256)            0         
_________________________________________________________________
flatten (Flatten)            (1, 9216)                 0         
_________________________________________________________________
dense (Dense)                (1, 4096)                 37752832  
_________________________________________________________________
dropout (Dropout)            (1, 4096)                 0         
_________________________________________________________________
dense_1 (Dense)              (1, 4096)                 16781312  
_________________________________________________________________
dropout_1 (Dropout)          (1, 4096)                 0         
_________________________________________________________________
dense_2 (Dense)              (1, 10)                   40970     
=================================================================
Total params: 58,299,082
Trainable params: 58,299,082
Non-trainable params: 0
_________________________________________________________________

2.手写数字势识别

AlexNet使用ImageNet数据集进行训练，但因为ImageNet数据集较大训练时间较长，我们仍用前面的MNIST数据集来演示AlexNet。读取数据的时将图像高和宽扩大到AlexNet使用的图像高和宽227。这个通过tf.image.resize_with_pad来实现。

2.1 数据读取

首先获取数据,并进行维度调整：

import numpy as np
# 获取手写数字数据集
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# 训练集数据维度的调整：N H W C
train_images = np.reshape(train_images,(train_images.shape[0],train_images.shape[1],train_images.shape[2],1))
# 测试集数据维度的调整：N H W C
test_images = np.reshape(test_images,(test_images.shape[0],test_images.shape[1],test_images.shape[2],1))

由于使用全部数据训练时间较长，我们定义两个方法获取部分数据，并将图像调整为227*227大小，进行模型训练：

# 定义两个方法随机抽取部分样本演示
# 获取训练集数据
def get_train(size):
    # 随机生成要抽样的样本的索引
    index = np.random.randint(0, np.shape(train_images)[0], size)
    # 将这些数据resize成227*227大小
    resized_images = tf.image.resize_with_pad(train_images[index],227,227,)
    # 返回抽取的
    return resized_images.numpy(), train_labels[index]
# 获取测试集数据 
def get_test(size):
    # 随机生成要抽样的样本的索引
    index = np.random.randint(0, np.shape(test_images)[0], size)
    # 将这些数据resize成227*227大小
    resized_images = tf.image.resize_with_pad(test_images[index],227,227,)
    # 返回抽样的测试样本
    return resized_images.numpy(), test_labels[index]

调用上述两个方法，获取参与模型训练和测试的数据集：

# 获取训练样本和测试样本
train_images,train_labels = get_train(256)
test_images,test_labels = get_test(128)

为了让大家更好的理解，我们将数据展示出来：

# 数据展示：将数据集的前九个数据集进行展示
for i in range(9):
    plt.subplot(3,3,i+1)
    # 以灰度图显示，不进行插值
    plt.imshow(train_images[i].astype(np.int8).squeeze(), cmap='gray', interpolation='none')
    # 设置图片的标题：对应的类别
    plt.title("数字{}".format(train_labels[i]))

结果为：

 

我们就使用上述创建的模型进行训练和评估。

2.2 模型编译

# 指定优化器，损失函数和评价指标
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01, momentum=0.0, nesterov=False)

net.compile(optimizer=optimizer,
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

2.3 模型训练

# 模型训练：指定训练数据，batchsize,epoch,验证集
net.fit(train_images,train_labels,batch_size=128,epochs=3,verbose=1,validation_split=0.1)

训练输出为：

Epoch 1/3
2/2 [==============================] - 3s 2s/step - loss: 2.3003 - accuracy: 0.0913 - val_loss: 2.3026 - val_accuracy: 0.0000e+00
Epoch 2/3
2/2 [==============================] - 3s 2s/step - loss: 2.3069 - accuracy: 0.0957 - val_loss: 2.3026 - val_accuracy: 0.0000e+00
Epoch 3/3
2/2 [==============================] - 4s 2s/step - loss: 2.3117 - accuracy: 0.0826 - val_loss: 2.3026 - val_accuracy: 0.0000e+00

2.4 模型评估

# 指定测试数据
net.evaluate(test_images,test_labels,verbose=1)

输出为：

4/4 [==============================] - 1s 168ms/step - loss: 2.3026 - accuracy: 0.0781
[2.3025851249694824, 0.078125]

如果我们使用整个数据集训练网络，并进行评估的结果：

[0.4866700246334076, 0.8395]

总结

• 知道AlexNet的网络架构
• 动手实现手写数字的识别

---

人工智能学习路线，记得收藏哦

零基础入门：

Python小白基础入门教程 Python入门到精通教程
零基础必备：全套Python教程_Python基础入门视频教程，零基础小白自学Python入门教程

python基础进阶：Python深入浅出进阶教程【敢信？】收藏=点赞十倍
Python实战Djongo项目：python企业级开发项目-手把手从0到1开发《美多商城》
mysql数据库：MySQL全套教程，MySQL从基础到黑马订单案例实战
机器学习算法：3天快速入门python机器学习
聚类算法：360°解读机器学习经典算法——聚类算法
数据挖掘：Python教程，4天快速入门Python数据挖掘，系统精讲+实战案例
Web服务器：Python高级语法进阶教程_python多任务及网络编程，从零搭建网站全套教程
180分钟爬虫入门：180分钟轻松获取疫情数据，Python爬虫入门课
Scrapy框架：Python爬虫基础，快速入门Scrapy爬虫框架
多线程：python多线程编程

人工智能入门：智能机器人软件开发教程基础，从helloworld到神经网络
人工智能深度学习：智能机器人软件开发教程基础，从helloworld到神经网络
图像与视觉处理：人工智能教程|零基础学习计算机视觉快速入门

---