回归算法

1 线性回归

1. 回归分析(Regression)

   回归分析是描述变量间关系的一种统计分析方法

   例：在线教育场景

   • 因变量 Y：在线学习课程满意度

   • 自变量 X：平台交互性、教学资源、课程设计

   预测性的建模技术，通常用于预测分析，预测的结果多为连续值（也可为离散值，二值）

2. 线性回归 (Linear regression)

   因变量和自变量之间是线性关系，就可以使用线性回归来建模
   $$y=b+m_1{x}_1+m_2{x}_2+\dots +m_n{x}_n$$
   其中 $m_1, m_2, \ldots, m_n $ 是各个特征的权重，$ x_1, x_2, \ldots, x_n $是对应的特征值。

   线性回归的目的即找到最能匹配(解释)数据的截距和斜率

3. 如何拟合数据

   假设只有一个因变量和自变量，每个训练样例表示 (𝑥𝑖 , 𝑦𝑖)

   用 ${\hat{y}}_i$ 表示根据拟合直线和 x𝑖 对 𝑦𝑖 的预测值：${\hat{y}}_i=b_1+b_2{x}_i$

   定义 $e_i=y_i-{\hat{y}}_i$ 为误差项

   

   目标：得到一条直线使得对于所有训练样例的误差项尽可能小

4. 线性回归的基本假设

   • 自变量与因变量间存在线性关系；
   • 数据点之间独立；
   • 自变量之间无共线性，相互独立；
   • 残差独立,等方差,且符合正态分布。

2 损失函数

1. 损失函数(loss function)

   损失函数（Loss Function）是用于衡量模型预测值与实际值之间差异的函数。

   • 均方误差（Mean Squared Error，MSE）：用于回归问题，计算预测值与实际值之间的平方差的平均值。
     $$\text{MSE}=\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$

   • 平均绝对误差（Mean Absolute Error，MAE）：也用于回归问题，计算预测值与实际值之间的绝对差的平均值。
     $$\text{MAE}=\frac{1}{n}\sum _{i=1}^n|y_i-{\hat{y}}_i|$$

2. 最小二乘法（Least Square, LS)

   为了求解最优的截距和斜率，可以转化为一个针对损失函数的凸优化问题，称为最小二乘法
   $$\underset{b_1,b_2}{\min }:\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2=\sum _{i=1}^n(y_i-b_1-b_{2}x{)}^2$$
   为求最小值，将上事对$b_1$，$b_2$求偏导，得到：
   $$\begin{gathered} b_2=\frac{{\sum }_{i=1}^n(x_i-\hat{x})(y_i-\hat{y})}{{\sum }_{i=1}^n(x_i-\hat{x}{)}^2} \\ {b}_1=\hat{y}-b_2\hat{x} \end{gathered}$$
   $\hat{x}$ 和 $\hat{y}$ 分别表示自变量和因变量的均值。

3. 梯度下降法(Gradient Descent, GD)

   沿着损失函数的梯度方向，通过不断更新模型参数来减小损失函数的值，直到达到损失函数的局部最小值或收敛到某个停止条件。

   • 初始化参数： 随机初始化模型的参数（权重 $b_2$ 和偏置 $b_1$）。

   • 计算梯度： 计算当前参数下损失函数关于每个参数的梯度（导数）。
     KaTeX parse error: Undefined control sequence: \part at position 8: \frac{\̲p̲a̲r̲t̲ ̲\sum_{i=1}^ne_i…

   • 更新参数： 沿着梯度的反方向调整参数，通过学习率 $\alpha$ 控制每次更新的步长。
     KaTeX parse error: Undefined control sequence: \part at position 19: …b-\alpha \frac{\̲p̲a̲r̲t̲ ̲\sum_{i=1}^ne_i…

   • 重复： 重复步骤2和3，直到满足停止条件，例如达到最大迭代次数或梯度接近零。

   • 输出： 返回最终的模型参数。

3 多元线性回归

1. 多元线性回归(Multiple Linear Regression)

   当因变量有多个时，我们可以用矩阵方式表达
   $$Y=X\beta +e$$
   $Y$ 为输出，$X$ 为输入矩阵，$\beta$ 为回归系数，$e$ 是误差项（残差）。

2. 损失函数

   误差项 $e=y-X\beta$

   损失函数 ${\sum }_{i=1}^n{e}_i^2=e^{\top }e$，$e^{\top }$表示转置

   求解得到 $\beta =(X^{\top }X{)}^{-1}{X}^{\top }y$

3. 实例：家庭花销预测

   记录了25个家庭每年在快销品和日常服务上总开销($Y$)，每年固定收入($X_2$) ,持有流动资产($X_3$)

   可以构建如下线性回归模型：
   $$y_i={\beta }_1+{\beta }_2{x}_{i2}+{\beta }_3{x}_{i3}+{ϵ}_i$$
   带入 $\beta =(X^{\top }X{)}^{-1}{X}^{\top }y$ ，计算得到 ${\beta }_1=36.789$，${\beta }_2=0.332$，${\beta }_3=0.125$。

   预测：如果一个家庭每年固定收入为 50K$、持有流动资产 100K$，则 预计一年将会花费
   $${\hat{y}}_i=36.79=0.332\ast 50+0.125\ast 100=65.96K$$

4. 以“误差平方和”为损失函数的优缺点

   • 优点
     • 损失函数是严格的凸函数，有唯一解
     • 求解过程简单且容易计算
   • 缺点
     • 结果对数据中的"离群点"(outlier)"非常敏感
     • 损失函数对于超过和低于真实值的预测是等价的

4 线性回归的相关系数

1. 相关系数r

   定义因变量和自变量之间的相关系数 r
   $$r=\frac{1}{n-1}\sum _{i=1}^n(\frac{x_i-\hat{x}}{s_x})(\frac{y_i-\hat{y}}{s_y})$$
   其中 $ \hat x$ 是 $X$ 的均值，$S_x$ 是 $X$ 的标准差$\sqrt{\frac{1}{n-1}\sum (x_i-\hat{x}{)}^2}$。

   协方差为$(\frac{x_i-\hat{x}}{s_x})(\frac{y_i-\hat{y}}{s_y})$，描述两个变量和Y的线性相关程度。

   

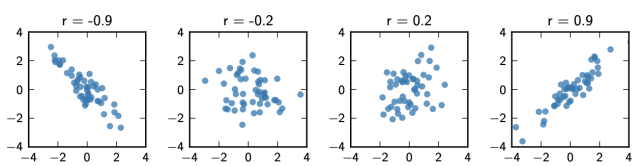
   相关系数r的绝对值越接近1，线性相关程度越高。

2. 决定系数(coefficient of determination)

   决定系数$R^2$ ,也称作判定系数、拟合优度。

   决定系数衡量了模型对数据的解释程度，y的波动有多少百分比能被x的波动所描述。
   $$R^2=1-\frac{\text{MSE}}{\text{VAR}}=\frac{{\sum }_i(y_i-\hat{y}{)}^2}{{\sum }_i(y_i-\bar{y}{)}^2}$$
   $y_i$ 为真实值，${\hat{y}}_i$ 为预测值，${\bar{y}}_i$ 为均值。$\text{MSE}$ 是均方误差，$\text{VAR}$是方差。

   $R^2$越接近1，表示回归分析中自变量对因变量的解释越好

   特别注意：变量相关 ≠ 存在因果关系。