目录
- 一、说明
- 二、MPC原理说明
- 三、分解算法的来源并显示关键特征,
- 四、C++ 实现说明
- 五、平衡 Q 和 R
- 六、资源下载地址
一、说明
以下文章介绍了应用模型预测控制器的简单控制系统方法。本文讨论了这种控制的基本机制,该机制适用于各种工程领域。
MPC 涉及对未来系统行为的预测(由一组方程描述的模型)。在优化过程中实现物理模型的所需位置(成本函数)。
您可以想象,具有系统动态模型(线性时不变 (LTI) 系统中的矩阵 A)的 MPC 模拟或预测模型在未来的位置或行为。然后,控制器计算一系列控制输入,以最小化预定义的成本函数,同时考虑所需的目标和约束。
出于本文的目的,我在 C++ 中准备了简单的模拟。其目的是展示可以轻松复制的原理,用于更高级的模型动力学。
二、MPC原理说明
我在C++中完全应用的标准模型预测控制(MPC)公式可以定义如下:
考虑一个具有以下状态空间表示的离散时间线性系统:
x
k
+
1
=
A
⋅
x
k
+
B
⋅
u
k
y
k
=
C
⋅
x
k
x_{k+1}=A \cdot x_k+B \cdot u_k \\ y_k=C\cdot x_k
xk+1=A⋅xk+B⋅ukyk=C⋅xk
这里
-
x k x_k xk 是时间步长 k 的状态向量,
-
U K UK UK 是时间步长 K 的控制输入向量,
-
y k y_k yk 是时间步长 k 的输出向量,
-
A 是状态转移矩阵(模型动力学),
-
B 是控制输入矩阵,
-
C 是输出矩阵。
模型预测控制 (MPC) 的目标是在满足系统约束的同时,在有限预测范围 N 上最小化成本函数。成本函数通常包括一个二次项,用于惩罚与参考轨迹和控制输入的偏差: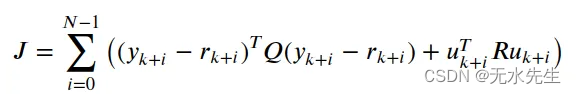
这里 -
N 是预测范围,
-
Q 是输出权重矩阵,
-
R 是控制输入权重矩阵,
-
r k + i r_{k+i} rk+i 是时间步长 k+i 的参考轨迹。
-
MPC问题被表述为优化问题,
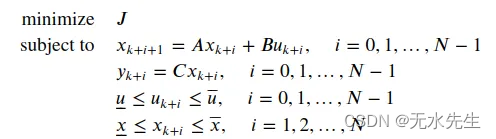
在这里,控制输入 u 和状态 x 位于下限和上限之下。
这个公式概述了线性离散时间系统的标准模型预测控制的数学结构,我在 C++ 模拟中应用了它。
在实践中(检查源代码),我们在每个时间步解决这个优化问题,以计算预测范围内的最优控制输入,然后将第一个控制输入应用于系统。
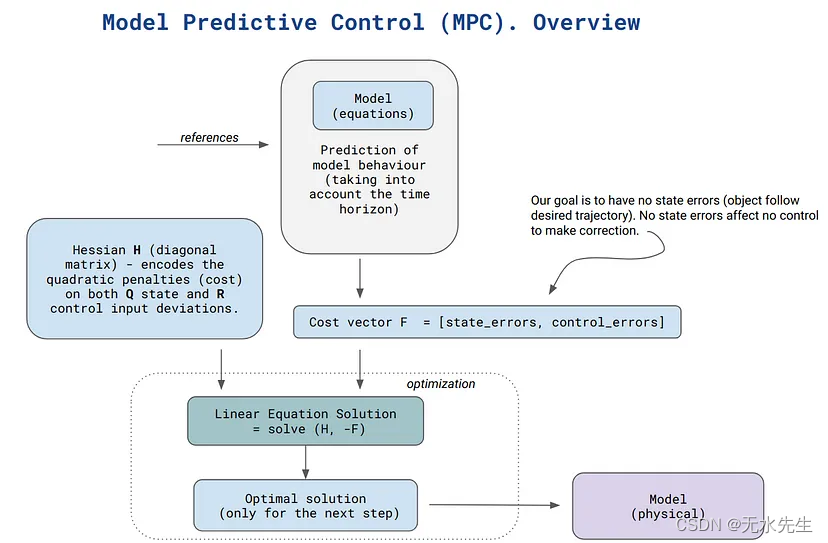
MPC 概述(作者)
三、分解算法的来源并显示关键特征,
- 海森矩阵 (H):通常,黑森矩阵是一个与二阶导数相关的数学概念,它提供有关多元函数曲率的信息。
在优化的情况下,我们使用 Hassian 来分析临界点(最小值或最大值)附近的目标函数的行为。在我们的特殊情况下,Hessian 对状态和控制输入偏差的二次惩罚进行编码。 - 成本向量 (F):向量是预测状态与所需参考状态的偏差和控制输入偏差的零值的组合。该向量表示成本函数的线性项,并指导优化过程以最小化成本。
- 优化过程:优化过程旨在找到控制输入的变化,使成本函数最小化。在二次优化问题的上下文中,这是通过求解由优化问题的最优条件产生的一组线性方程来实现的。
我们求解由最优条件形成的线性方程。此操作计算应应用于当前控制输入的控制输入的最佳变化,以便使系统状态更接近所需的基准电压源,同时将成本降至最低。
四、C++ 实现说明
请务必仔细查看我的 C++ 实现并考虑这一行,
Eigen::VectorXd control_input_delta = H.colPivHouseholderQr().solve(-f);
这行代码正在求解 H x = − f Hx=-f Hx=−f 形式的线性方程,其中 H 是矩阵,f 是向量。该操作使用QR分解和列枢轴执行,这是一种求解线性系统的数值方法。以下是分步分解:
- 矩阵 H 和向量 f:
H 是表示线性方程组的方阵。
f 是一个向量,运算涉及它的否定 (-f),它用作线性方程的右侧。 - 列旋转QR分解:
colPivHouseholderQr()计算矩阵 H 的 QR 分解与列透视。
在 QR 分解中,矩阵 H 被分解为两个矩阵 Q 和 R,其中 Q 是正交矩阵(意味着 Q T ⋅ Q = I Q^T\cdot Q=I QT⋅Q=I其中 I I I是单位矩阵),R 是上三角矩阵。
列枢轴是一种用于提高分解的数值稳定性的技术,特别是对于接近奇异或条件不良的矩阵。
- 求解线性系统:
该运算用于使用 H 的 QR 分解求解线性系统 Hx = −f。.solve(-f)
从数学上讲,解 x 可以通过以下方式找到:
x = Q − 1 ⋅ R − 1 ( − f ) x=Q^{-1}\cdot R^{-1}(-f) x=Q−1⋅R−1(−f)
由于 Q 是正交的, Q − 1 = Q T Q^{-1}= Q^{T} Q−1=QT
简化计算。解 x 被赋值给变量control_input_delta ,其类型为Eigen::VectorXd
- 数学表示:
整个运算在数学上可以表示为使用QR分解和列枢轴求解方程 H x = − f Hx = −f Hx=−f中的x:
x = H − 1 ( − f ) x=H^{-1} (−f) x=H−1(−f)
或者更明确地说:
x
=
(
Q
⋅
R
)
−
1
(
−
f
)
x
=
(
R
)
−
1
⋅
Q
T
(
−
f
)
x=(Q \cdot R)^{-1}(-f) \\ x=(R )^{-1}\cdot Q^{T}(-f)
x=(Q⋅R)−1(−f)x=(R)−1⋅QT(−f)
- Q矩阵
定义:Q 矩阵是一个方形、对称且通常为正的半定矩阵,用于 MPC 的成本函数,用于权衡跟踪参考状态或设定值的重要性。
在成本函数中的作用:在 MPC 的目标函数中,Q 矩阵乘以状态误差(预测状态和期望状态之间的差值)。
成本函数的这一部分通常写为 ( x − x r e f ) T Q ( x − x r e f ) (x−x_{ref})TQ(x−x_{ref}) (x−xref)TQ(x−xref)其中 x 是预测状态, x r e f x_{ref} xref 是期望状态或参考。
目的:Q 矩阵旨在惩罚偏离期望状态的情况。通过调整 Q 中的权重,您可以指定状态向量的哪些方面更需要调节。例如,某些状态的 Q 权重较高意味着控制器将优先最小化这些状态中的错误。 - R矩阵
定义:R 矩阵和 Q 一样,是一个正方形、对称且通常为正定矩阵。它在 MPC 成本函数中用于权衡控制工作量或控制输入。
成本函数中的作用:R矩阵是涉及控制输入的目标函数项的一部分。这通常写成 uTRu,其中 u 是控制输入向量。
目的:R矩阵的作用是惩罚过度的控制行为。R 中的权重越大,意味着对大控制输入的惩罚越大,鼓励控制器使用较小的输入,从而可能导致更平滑的控制操作。这对于防止执行器(电机驱动器)上的过多设置或对于不需要或不安全的大控制输入的系统非常重要。
五、平衡 Q 和 R
Q 和 R 矩阵中的相对值定义了跟踪参考轨迹(状态精度)的重要性和最小化控制工作量之间的权衡。这种权衡是 MPC 控制器设计的核心:
高 Q 值、低 R:将状态跟踪准确性置于控制工作之上,从而采取积极的控制措施。
低 Q 值、高 R:优先考虑最大程度地减少控制工作,可能以牺牲跟踪性能为代价。
下面,我提供了可以在机器上运行的模拟的输出。
下面的第一个仿真提供了有关 MPC 如何执行以接近所需恒定位置(值)的信息。
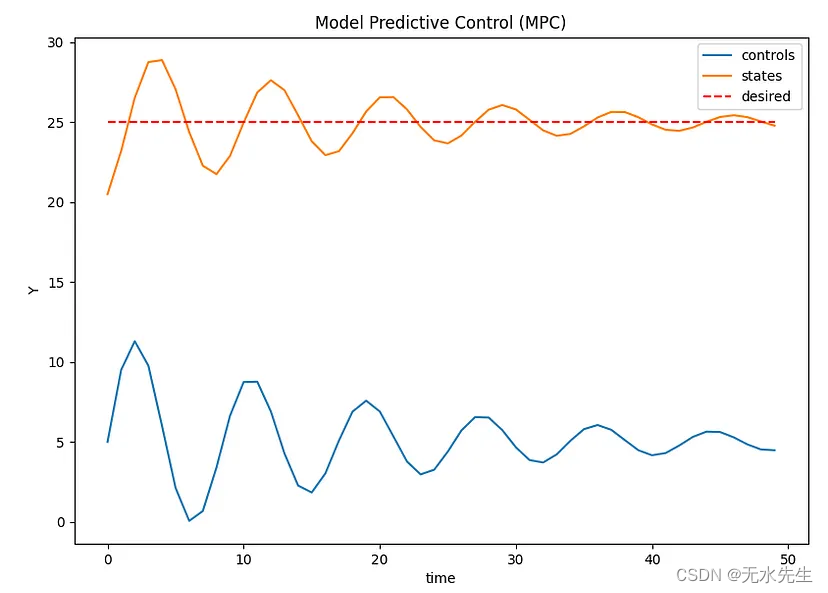
MPC 性能。模拟 1
您可以运行的第二个仿真提供 MPC 性能输出,而所需的轨迹具有正弦函数的形状。成本函数(矩阵值 Q、R)的正确选择会影响状态以及系统如何随时间推移而稳定。在这里插入图片描述
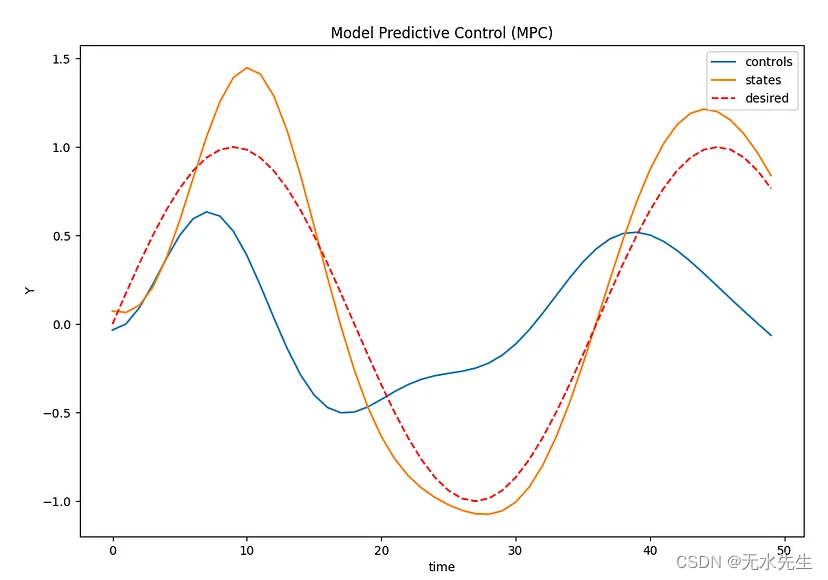 MPC 性能。模拟 2。感谢您的阅读。
MPC 性能。模拟 2。感谢您的阅读。
六、资源下载地址
本文相关的代码下载地址:
https://download.csdn.net/download/gongdiwudu/88823951
关于matplotlib的相关资源地址:
https://download.csdn.net/download/gongdiwudu/88821722