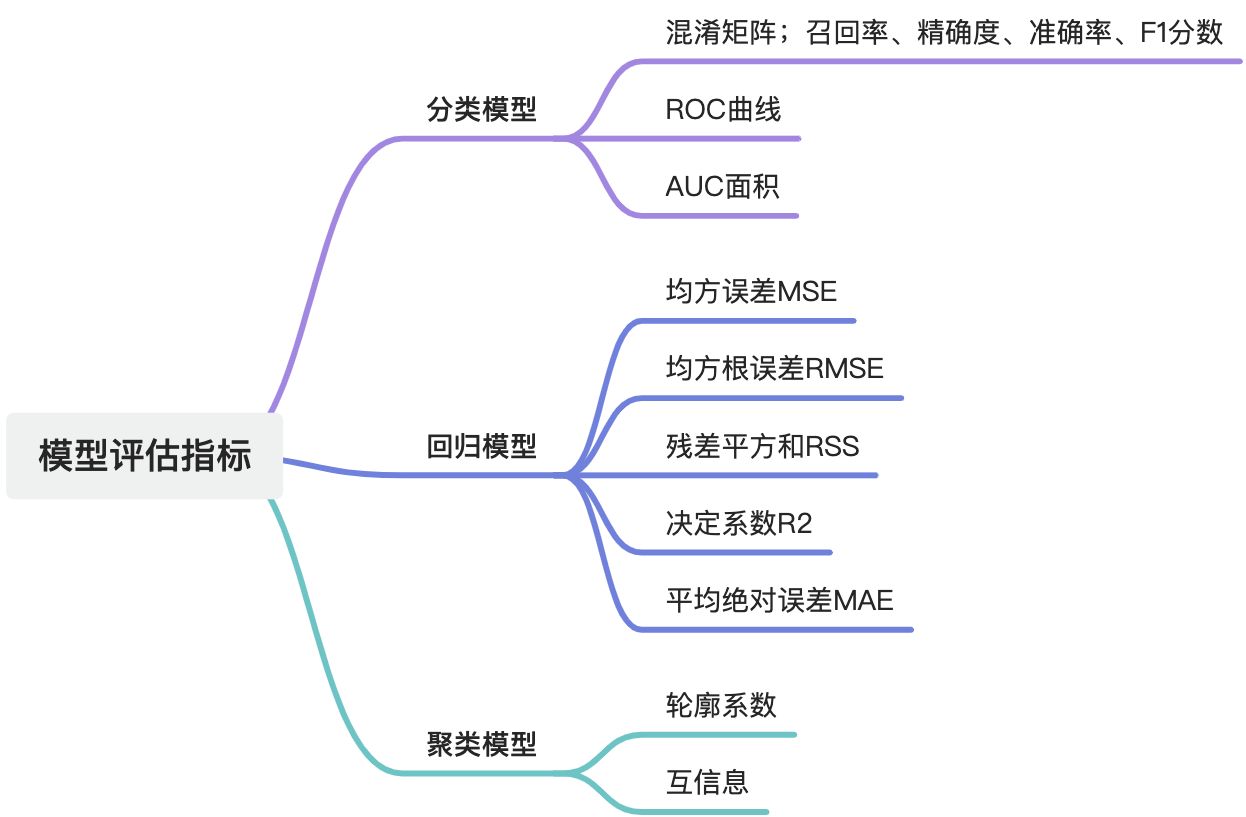
分类模型
混淆矩阵
混淆矩阵(Confusion Matrix)是一种用于评估分类模型性能的表格,它可以显示模型预测结果与真实标签之间的关系。混淆矩阵的行表示实际类别,列表示预测类别。
一个典型的二分类混淆矩阵包含四个单元格,分别代表了真阳性(True Positive,TP)、假阳性(False Positive,FP)、真阴性(True Negative,TN)和假阴性(False Negative,FN):
Predicted Positive
Predicted Negative
Actual Positive
TP
FN
Actual Negative
FP
TN
\begin{matrix} & \text{Predicted Positive} & \text{Predicted Negative} \\ \text{Actual Positive} & \text{TP} & \text{FN} \\ \text{Actual Negative} & \text{FP} & \text{TN} \\ \end{matrix}
Actual PositiveActual NegativePredicted PositiveTPFPPredicted NegativeFNTN
其中,TP 表示模型将正例预测为正例的数量,FN 表示模型将正例预测为负例的数量,FP 表示模型将负例预测为正例的数量,TN 表示模型将负例预测为负例的数量。
混淆矩阵可以帮助我们对分类模型的性能进行更细致的评估,例如计算准确率、精确率、召回率和 F1 分数等指标。
from sklearn.metrics import confusion_matrix
# 示例数据
y_true = [1, 0, 1, 1, 0, 1]
y_pred = [1, 1, 1, 0, 0, 1]
# 计算混淆矩阵
cm = confusion_matrix(y_true, y_pred)
print("Confusion Matrix:")
print(cm)
召回率
召回率(Recall),也称为真正例率(True Positive Rate,TPR)或灵敏度(Sensitivity),是衡量分类模型对正例样本的识别能力的指标。它表示模型正确识别出的正例样本数量占所有实际正例样本数量的比例。
召回率的计算公式如下:
R
e
c
a
l
l
=
T
P
T
P
+
F
N
Recall = \frac{TP}{TP + FN}
Recall=TP+FNTP
其中,TP 表示真阳性(模型将正例预测为正例的数量),FN 表示假阴性(模型将正例预测为负例的数量)。
召回率的取值范围在 0 到 1 之间,越接近 1 表示模型对正例样本的识别能力越好。
from sklearn.metrics import recall_score
# 示例数据
y_true = [1, 0, 1, 1, 0, 1]
y_pred = [1, 1, 1, 0, 0, 1]
# 计算召回率
recall = recall_score(y_true, y_pred)
print("Recall:", recall)
精确度
精确度(Precision)是分类模型的一个指标,用于衡量模型在预测为正例的样本中,有多少是真正的正例。精确度与召回率一起评估分类模型的性能。
精确度的计算公式如下:
P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
Precision = \frac{TP}{TP + FP}
Precision=TP+FPTP
其中,TP 表示真阳性(模型将正例预测为正例的数量),FP 表示假阳性(模型将负例预测为正例的数量)。
精确度的取值范围在 0 到 1 之间,越接近 1 表示模型在预测为正例的样本中有更高的准确率。
from sklearn.metrics import precision_score
# 示例数据
y_true = [1, 0, 1, 1, 0, 1]
y_pred = [1, 1, 1, 0, 0, 1]
# 计算精确度
precision = precision_score(y_true, y_pred)
print("Precision:", precision)
准确率
准确率(Accuracy)是分类模型的一个指标,用于衡量模型在所有样本中正确分类的比例。它是一个综合评估模型性能的指标。
准确率的计算公式如下:
A
c
c
u
r
a
c
y
=
T
P
+
T
N
T
P
+
T
N
+
F
P
+
F
N
Accuracy = \frac{TP + TN}{TP + TN + FP +FN}
Accuracy=TP+TN+FP+FNTP+TN
其中,TP 表示真阳性(模型将正例预测为正例的数量),TN 表示真阴性(模型将负例预测为负例的数量),FP 表示假阳性(模型将负例预测为正例的数量),FN 表示假阴性(模型将正例预测为负例的数量)。
准确率的取值范围在 0 到 1 之间,越接近 1 表示模型的分类准确率越高。
from sklearn.metrics import accuracy_score
# 示例数据
y_true = [1, 0, 1, 1, 0, 1]
y_pred = [1, 1, 1, 0, 0, 1]
# 计算准确率
accuracy = accuracy_score(y_true, y_pred)
print("Accuracy:", accuracy)
F1分数
F1 分数是一个综合评价分类模型性能的指标,综合考虑了精确度(Precision)和召回率(Recall)。F1 分数是精确度和召回率的调和平均数。
F1 分数的计算公式如下:
F
1
=
2
×
P
r
e
c
i
s
i
o
n
×
R
e
c
a
l
l
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
F1 = 2 \times \frac{Precision \times Recall}{Precision + Recall}
F1=2×Precision+RecallPrecision×Recall
其中,Precision 是精确度,Recall 是召回率。
F1 分数的取值范围在 0 到 1 之间,越接近 1 表示模型的性能越好。F1 分数相比于单独的精确度和召回率能够更全面地评价模型的性能。
from sklearn.metrics import f1_score
# 示例数据
y_true = [1, 0, 1, 1, 0, 1]
y_pred = [1, 1, 1, 0, 0, 1]
# 计算 F1 分数
f1 = f1_score(y_true, y_pred)
print("F1 Score:", f1)
ROC曲线与AUC面积
ROC 曲线(Receiver Operating Characteristic Curve)是用于评估分类模型性能的一种常用工具。ROC 曲线以假正例率(False Positive Rate, FPR)为横坐标,真正例率(True Positive Rate, TPR)为纵坐标,将模型在不同阈值下的性能表现可视化。
假正例率(FPR)是指所有实际为负例样本中,被错误地划分为正例的样本所占比例,计算公式为:
F
P
R
=
F
P
F
P
+
T
N
FPR = \frac{FP}{FP + TN}
FPR=FP+TNFP
真正例率(TPR)是指所有实际为正例样本中,被正确地划分为正例的样本所占比例,即召回率,计算公式为:
T
P
R
=
T
P
T
P
+
F
N
TPR = \frac{TP}{TP + FN}
TPR=TP+FNTP
在 ROC 曲线上,理想情况下,模型的曲线会尽可能地靠近左上角,这意味着模型在各种阈值下都能保持较低的假正例率的同时获得较高的真正例率,即具有较高的性能。
ROC 曲线下的面积(Area Under the ROC Curve, AUC)是一个常用的性能评估指标,用于衡量分类模型在不同阈值下的性能表现。AUC 值越接近 1,表示模型的性能越好;如果 AUC 值接近 0.5,则表示模型的性能与随机猜测相近;如果 AUC 值小于 0.5,则表示模型的性能比随机猜测还差。
import numpy as np
from sklearn.metrics import roc_curve, auc, roc_auc_score
import matplotlib.pyplot as plt
# 生成随机示例数据
np.random.seed(42)
y_true = np.random.randint(0, 2, size=100)
y_scores = np.random.rand(100)
# 计算 ROC 曲线
fpr, tpr, thresholds = roc_curve(y_true, y_scores)
roc_auc = auc(fpr, tpr)
# 计算 ROC 曲线下的面积
auc_score = roc_auc_score(y_true, y_scores)
print("AUC Score:", auc_score)
# 绘制 ROC 曲线
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC) Curve')
plt.legend(loc='lower right')
plt.show()

回归模型
均方误差MSE
均方误差(MSE)是衡量预测值与实际观测值之间差异的一种方法,常用于评估模型的性能。MSE 是预测误差的平方的平均值,计算方式如下:
MSE = (1/n) * Σ(yᵢ - ŷᵢ)²
其中,n 是样本数量,yᵢ 是实际观测值,ŷᵢ 是对应的预测值。MSE 的值越小,表示模型的预测能力越好。
MSE 的优点之一是它惩罚了较大的误差,因为误差被平方了。这意味着在计算 MSE 时,较大的误差将对最终结果有更大的影响,这有助于更好地识别模型的预测能力。
然而,需要注意的是,MSE 有一个缺点,即它对异常值(离群值)比较敏感,因为它是对误差的平方求平均。这意味着如果存在异常值,MSE 可能会受到其影响,导致对模型性能的评估不准确。
import numpy as np
# 示例数据
actual_values = np.array([1, 2, 3, 4, 5])
predicted_values = np.array([1.2, 2.1, 2.9, 4.2, 5.3])
# 计算均方误差
mse = np.mean((actual_values - predicted_values) ** 2)
print("Mean Squared Error:", mse)
均方根误差RMSE
均方根误差(Root Mean Square Error,RMSE)是一种常用的衡量预测模型误差的指标。在统计学和机器学习领域中经常用于评估模型的预测性能。RMSE 表示观测值与预测值之间的差异程度,其计算公式如下:
RMSE
=
1
n
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
\text{RMSE} = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}
RMSE=n1∑i=1n(yi−y^i)2
其中,n是样本数量,
y
i
y_i
yi是观测值,
y
^
i
\hat{y}_i
y^i是对应的预测值。RMSE 的计算方法是将每个观测值与其对应的预测值之差的平方求和,然后取平均值,最后再对结果进行平方根操作。
RMSE 的值越小,表示模型的预测能力越好,因为它表示了观测值与预测值之间的平均偏差。
import numpy as np
# 示例数据
actual_values = np.array([1, 2, 3, 4, 5])
predicted_values = np.array([1.2, 2.1, 2.9, 4.2, 5.3])
# 计算均方误差
mse = np.mean((actual_values - predicted_values) ** 2)
# 计算均方根误差
rmse = np.sqrt(mse)
print("Root Mean Squared Error:", rmse)
残差平方和RSS
残差平方和(Residual Sum of Squares,RSS)是另一个常用于评估模型拟合优度的指标。它表示模型预测值与实际观测值之间的差异的平方和,通常用于线性回归模型的评估。
残差平方和的计算公式如下:
RSS
=
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
\text{RSS} = \sum_{i=1}^{n}(y_i - \hat{y}_i)^2
RSS=∑i=1n(yi−y^i)2
其中,n是样本数量,
y
i
y_i
yi是观测值,
y
^
i
\hat{y}_i
y^i是对应的预测值。计算方法是将每个观测值与其对应的预测值之差的平方求和。
RSS 越小表示模型的拟合程度越好,因为它表示了观测值与预测值之间的总体偏差的平方和越小。
import numpy as np
# 示例数据
actual_values = np.array([1, 2, 3, 4, 5])
predicted_values = np.array([1.2, 2.1, 2.9, 4.2, 5.3])
# 计算残差
residuals = actual_values - predicted_values
# 计算残差平方和
rss = np.sum(residuals**2)
print("Residual Sum of Squares (RSS):", rss)
决定系数 R 2 R^2 R2
决定系数(Coefficient of Determination),通常用
R
2
R^2
R2表示,是一种用于衡量一个回归模型的拟合优度的统计量。它表示模型能够解释的目标变量方差的比例。
决定系数的计算公式如下:
R
2
=
1
−
R
S
S
T
S
S
R^2 = 1 - \frac{RSS}{TSS}
R2=1−TSSRSS
其中,RSS是残差平方和(Residual Sum of Squares),TSS是总平方和(Total Sum of Squares)。
总平方和表示目标变量(因变量)的方差,计算方法为观测值与观测值的均值之差的平方和:
T
S
S
=
∑
i
=
1
n
(
y
i
−
y
ˉ
)
2
TSS = \sum_{i=1}^{n}(y_i - \bar{y})^2
TSS=∑i=1n(yi−yˉ)2
其中,n是样本数量,
y
i
y_i
yi是观测值,
y
ˉ
\bar{y}
yˉ是观测值的均值。
决定系数
R
2
R^2
R2的取值范围在 0 到 1 之间,越接近1表示模型拟合得越好,即模型能够解释目标变量方差的比例越高。当
R
2
R^2
R2等于1时,表示模型完美拟合数据,解释了目标变量方差的100%。而当
R
2
R^2
R2等于0时,表示模型无法解释目标变量的变异性,预测值与真实值之间的差异全部由随机误差导致。
from sklearn.metrics import r2_score
import numpy as np
# 示例数据
actual_values = np.array([1, 2, 3, 4, 5])
predicted_values = np.array([1.2, 2.1, 2.9, 4.2, 5.3])
# 计算决定系数 R^2
r_squared = r2_score(actual_values, predicted_values)
print("Coefficient of Determination (R^2):", r_squared)
平均绝对误差MAE
平均绝对误差(Mean Absolute Error,MAE)是一种衡量预测模型误差的指标,它表示观测值与预测值之间的绝对差异的平均值。
MAE 的计算公式如下:
MAE
=
1
n
∑
i
=
1
n
∣
y
i
−
y
^
i
∣
\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} \left| y_i - \hat{y}_i \right|
MAE=n1∑i=1n∣yi−y^i∣
其中,n是样本数量,
y
i
y_i
yi是观测值,
y
^
i
\hat{y}_i
y^i是对应的预测值。
MAE 的计算方法是将每个观测值与其对应的预测值之差取绝对值后求和,然后再取平均值。
MAE 越小表示模型的预测能力越好,因为它表示了观测值与预测值之间的平均绝对偏差。
import numpy as np
# 示例数据
actual_values = np.array([1, 2, 3, 4, 5])
predicted_values = np.array([1.2, 2.1, 2.9, 4.2, 5.3])
# 计算绝对误差
absolute_errors = np.abs(actual_values - predicted_values)
# 计算平均绝对误差
mae = np.mean(absolute_errors)
print("Mean Absolute Error (MAE):", mae)
聚类模型
轮廓系数
轮廓系数(Silhouette Coefficient)是一种用于评估聚类结果的指标,它同时考虑了簇内的紧密度和簇间的分离度。轮廓系数的取值范围在 -1 到 1 之间,数值越接近 1 表示聚类结果越好,数值越接近 -1 则表示聚类结果越差。
轮廓系数的计算方式如下:
对于每个样本 i:
计算样本 i 到同簇其他样本的平均距离,记作
a
i
a_i
ai,
a
i
a_i
ai 越小表示样本 i 越应该被分到该簇。
计算样本 i 到其他某个簇中所有样本的平均距离,取最小值,记作
b
i
b_i
bi,即样本 i 与最近其他簇的平均距离,
b
i
b_i
bi 越大表示样本 i 越不应该被分到其他簇。
根据以下公式计算样本 i 的轮廓系数:
silhouette
i
=
b
i
−
a
i
max
(
a
i
,
b
i
)
\text{silhouette}_i = \frac{b_i - a_i}{\max(a_i, b_i)}
silhouettei=max(ai,bi)bi−ai
最后,对所有样本的轮廓系数取平均,即为整个数据集的轮廓系数。
在实际应用中,轮廓系数可以用来选择最优的聚类数目或者比较不同聚类算法的性能。
from sklearn.metrics import silhouette_score
from sklearn.cluster import KMeans
import numpy as np
# 示例数据
X = np.array([[1, 2], [2, 3], [6, 7], [8, 9]])
# 使用 KMeans 聚类算法进行聚类
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
labels = kmeans.labels_
# 计算轮廓系数
silhouette_avg = silhouette_score(X, labels)
print("Silhouette Score:", silhouette_avg)
互信息
互信息(Mutual Information)是一种用于度量两个随机变量之间的相关性的指标。它衡量的是在已知一个随机变量的情况下,另一个随机变量的不确定性减少了多少。
互信息的计算公式如下:
I
(
X
;
Y
)
=
∑
y
∈
Y
∑
x
∈
X
p
(
x
,
y
)
log
(
p
(
x
,
y
)
p
(
x
)
p
(
y
)
)
I(X;Y) = \sum_{y \in Y} \sum_{x \in X} p(x, y) \log \left( \frac{p(x, y)}{p(x)p(y)} \right)
I(X;Y)=∑y∈Y∑x∈Xp(x,y)log(p(x)p(y)p(x,y))
其中,
I
(
X
;
Y
)
I(X;Y)
I(X;Y)表示变量
X
X
X和
Y
Y
Y之间的互信息,
p
(
x
,
y
)
p(x, y)
p(x,y)是变量
X
X
X和
Y
Y
Y同时取值
x
x
x和
y
y
y的概率,
p
(
x
)
p(x)
p(x)和
p
(
y
)
p(y)
p(y)分别是变量
X
X
X和
Y
Y
Y单独取值
x
x
x和
y
y
y的概率。
互信息越大表示变量之间的相关性越强,互信息为 0 表示两个变量之间没有相关性。
from sklearn.metrics import mutual_info_score
# 示例数据
X = [1, 2, 3, 4, 5]
Y = [1, 2, 2, 3, 3]
# 计算互信息
mutual_info = mutual_info_score(X, Y)
print("Mutual Information:", mutual_info)

![[Angular 基础] - 指令(directives)](https://img-blog.csdnimg.cn/direct/1801a18ad0fe4e7e9722b308055506e3.png)



![[office] excel如何计算毛重和皮重的时间间隔 excel计算毛重和皮重时间间隔方法 #笔记#学习方法](https://img-blog.csdnimg.cn/img_convert/fb5d20f8a614730f4c04d57a84b97f7e.jpeg)