二叉树中的最大路径和

news2024/9/22 20:36:11

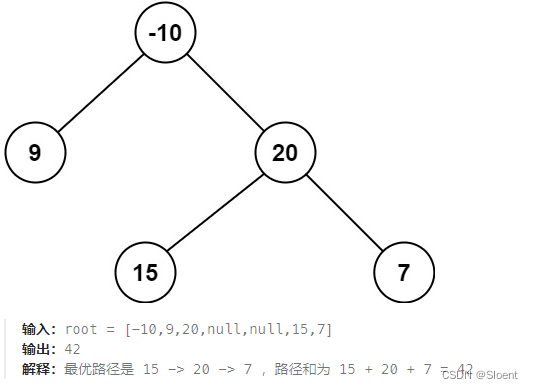
124. 二叉树中的最大路径和 - 力扣（LeetCode）

思路

路径每到一个节点，有 3 种选择：1. 停在当前节点。2. 走到左子节点。3. 走到右子节点。
走到子节点，又面临这 3 种选择，递归适合处理这种规模不同的同一问题。
注意，不能走进一个分支又掉头回来走另一个分支，路径会重叠，不符合题目要求。

定义递归函数

对于一个父节点，它关心自己走入一个子树，从中捞取的最大收益，不关心具体怎么走。

定义dfs函数：返回当前子树能向父节点“提供”的最大路径和。即，一条从父节点延伸下来的路径，能在当前子树中捞取的最大收益。分三种情况：

路径停在当前子树的根节点，在当前子树的最大收益：root.val
走入左子树，在当前子树的最大收益：root.val + dfs(root.left)
走入右子树，在当前子树的最大收益：root.val + dfs(root.right)

这对应了前面所说的三种选择，最大收益取三者最大：root.val+max(0, dfs(root.left), dfs(root.right))

再次提醒: 一条从父节点延伸下来的路径，不能走入左子树又掉头走右子树，不能两头收益。

当遍历到null节点时，null 子树提供不了收益，返回 0。
如果某个子树 dfs 结果为负，走入它，收益不增反减，该子树就没用，需杜绝走入，像对待 null 一样让它返回 0。

子树中的内部路径要包含根节点

题意可知，最大路径和，是可能产生于其中一个子树中的，就好比下图左一。
所以每递归一个子树，都求一下当前子树内部的最大路径和，见下图右一的绿字，从中比较出最大的。

注意: 一个子树内部的路径，要包含当前子树的根节点。如果不包含，那还算什么属于当前子树的路径，那就是当前子树的子树的内部路径了。

所以，一个子树内部的最大路径和 = 左子树提供的最大路径和 + 根节点值 + 右子树提供的最大路径和。

即 dfs(root.left)+root.val+dfs(root.right)

代码

时间复杂度 O(N)，每个节点都要遍历，空间复杂度是 O(H)，递归树的深度。

class Solution {
	int result = Integer.MIN_VALUE;
	public int maxPathSum(TreeNode root) {
		dfs(root);
		return result;
	}
	
	private int dfs(TreeNode root) { 
		// 如果当前节点为叶子节点，那么对父亲贡献为 0
		if(root == null) return 0;
		
		// 如果不是叶子节点，计算当前节点的左右孩子对自身的贡献left和right
		// 遇到负数不返回负值
		int left = Math.max(dfs(root.left), 0);
        int right = Math.max(dfs(root.right), 0);
		
		// 更新最大值，就是当前节点的val 加上左右节点的贡献。
		result = Math.max(result, root.val + left + right);
		
		// 计算当前节点能为父亲提供的最大贡献，必须是把 val 加上
		return root.val + Math.max(left, right);
	}
}