幻方(Magic Square)
幻方概述
什么是幻方呢?幻方(Magic Square)就是指在n×n(n行n列)的方格里填上一些连续的数字,使任意一行、任意一列和对角线上的数字的和都相等。例如有3×3的3行3列的幻方叫三阶幻方,4×4的4行4列的幻方叫四阶幻方,5×5的5行5列的幻方叫五阶幻方等等。
幻方最早记载于中国公元前500年的春秋时期《大戴礼》中,这说明中国人民早在2500年前就已经知道了幻方的排列规律。除了“河图”,中国古代还有“洛书”之说,相传在大禹治洪水时,洛水中浮出一只大乌龟,背上有图有字,人们称之为“洛书”。
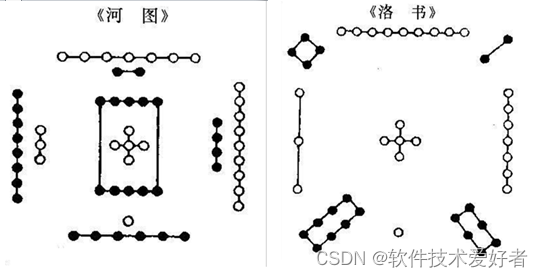
在幻方中每行、每列、每条对角线上各数的和都相等,这个和称为“幻和”。
幻和 = 总数和 ÷ 阶数
奇数幻方中,中间数 = 幻和 ÷ 阶数
由1、2、3、……等连续自然数生成的幻方为基本幻方。在此基础上各数再加或减一个相同的数,可组成由零或负数组成的新幻方。也就是说,编排n阶幻方时,不一定非要从1开始,只要是这些数能构成等差数列就可以了。
一般我们把奇数×奇数的幻方叫奇阶幻方,偶数×偶数的幻方叫偶阶幻方,填奇阶幻方和偶阶幻方的有着不同的方法。
一、奇阶幻方通用构造方法
口诀(又称为罗伯法):
一居上行正中央,
依次斜填切莫忘,
上出框界往下写,
右出框时左边放,
重复便在下格填,
出角重复一个样。
解释:
把1(或最小的数)放在第一行正中; 按以下规律排列剩下的(n×n-1)个数:
1、每一个数放在前一个数的右上一格;
2、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;
3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;
4、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;
5、如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
三阶幻方为例子:
一居上行正中央——数字 1 放在首行最中间的格子中。如下图:
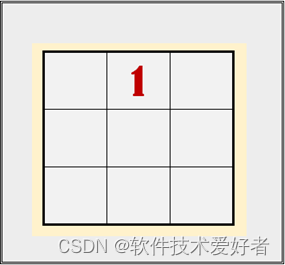
依次斜填切莫忘——向右上角斜行,依次填入数字。如下图:
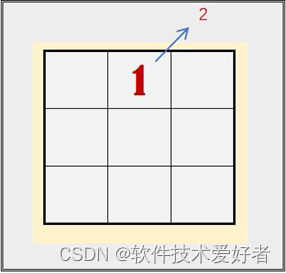
上出框界往下写——如果出了上框边界,就将数字填在该列最下面空格里。如下图:

右出框时左边放——如果出了右框边界,就将数字填在该行最左空格里。如下图:
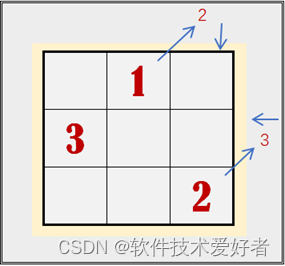
重复便在下格填——如果右上格子已填数字,就填在前一数字下面空格里。如下图:

出角重复一个样——如果朝右上角出框界,和“重复”的情况做同样处理。如下图:
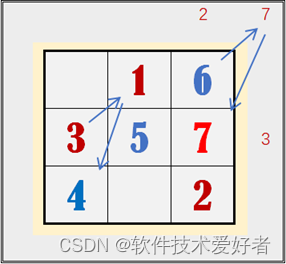
最后8和9按照右出界、上出界的方法填写,如下图:
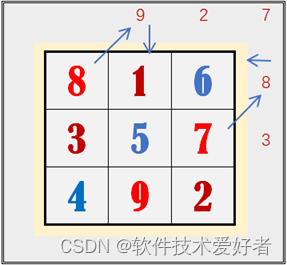
完成!
按照这种方式,完成后,做镜像或旋转对称,可得到实际相同的其他填法,如:

用该填法得到的5阶幻方:
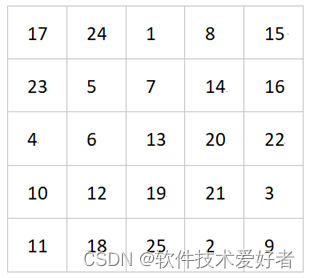
7阶幻方:
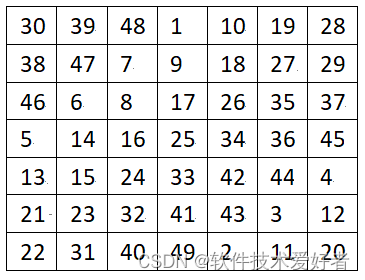
二、偶数阶幻方
偶阶幻方的概念:一个n阶幻方,当n为偶数时,我们称幻方为偶阶幻方。
偶阶幻方分为双偶幻方和单偶幻方。当n可以被4整除时,我们称该偶阶幻方为双偶阶幻方,如8阶、12阶、16阶等;当n不可被4整除时,我们称该偶阶幻方为单偶阶幻方(即4M+2式幻方),如6阶、10阶、14阶等。偶数阶幻方的构造方法由此分为两类:双偶阶幻方和单偶阶幻方。
待续










![[SOAP] SOAP协议基础知识](https://img-blog.csdnimg.cn/direct/a6c6d082e8af4721a9f1e7faee5badee.png)