"The only limit to our realization of tomorrow will be our doubts of today."
- Franklin D. Roosevelt

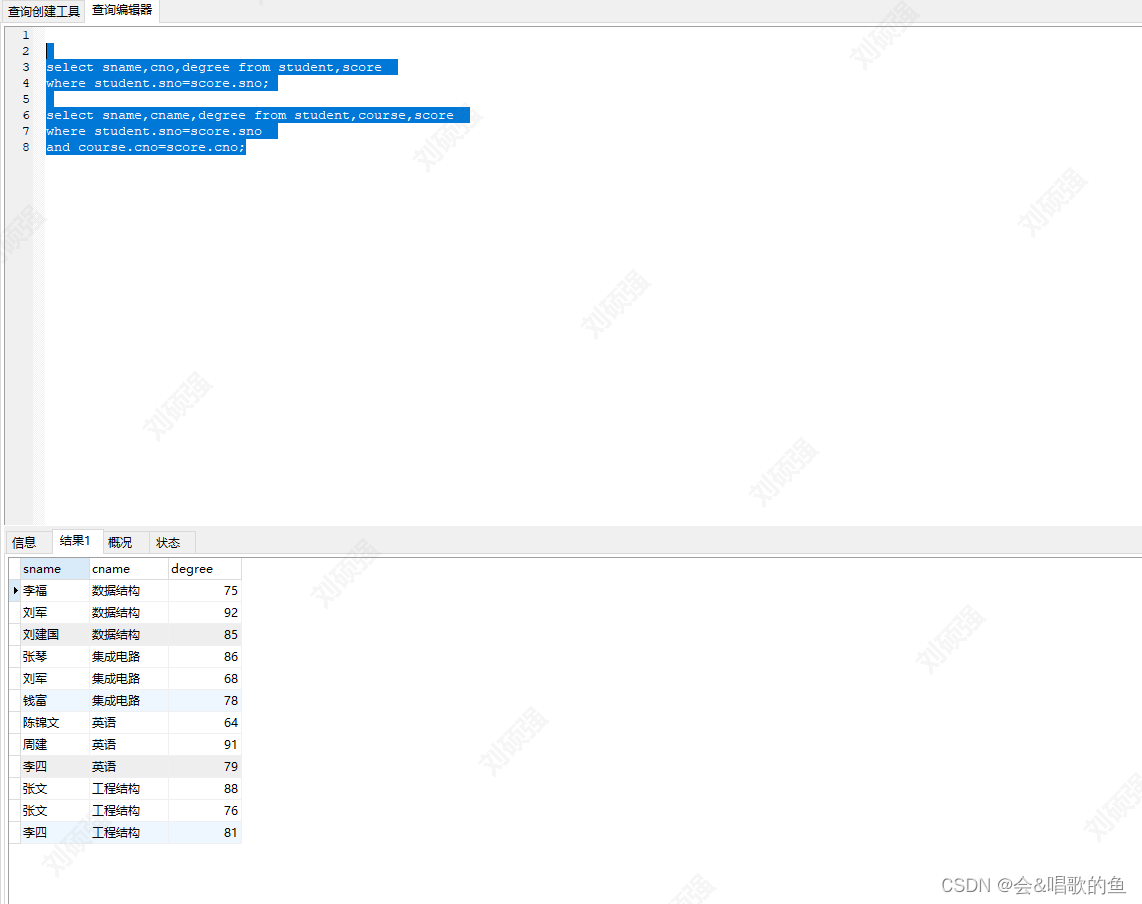
1. 题目描述

2. 题目分析与解析
2.1 思路一——暴力求解
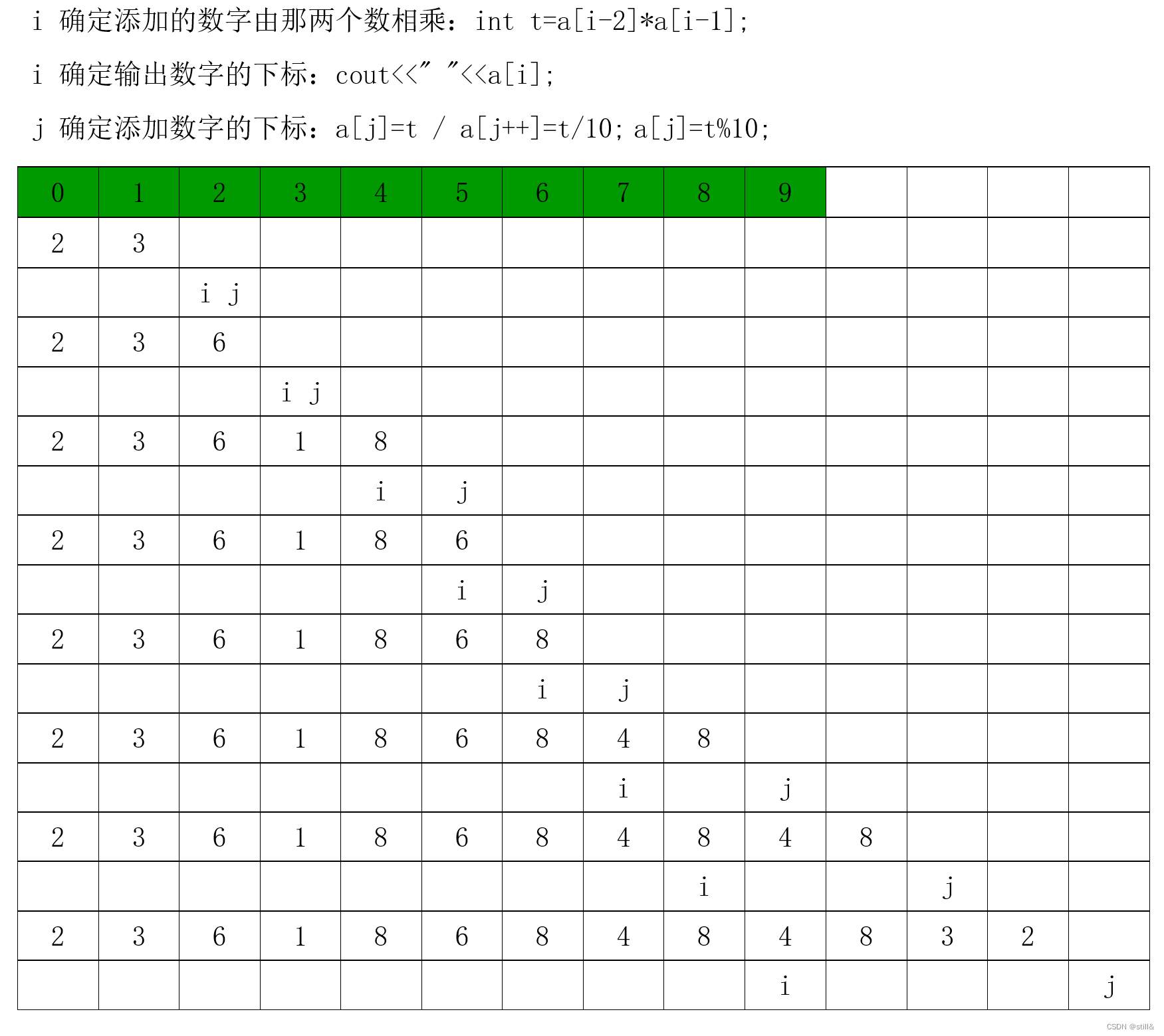
暴力求解的思路就是通过两次for循环,外层循环遍历整个数组,内层循环遍历剩下的部分,也可以将其理解为双指针。

但是这种解法的时间复杂度是O(n^2),是很高的。所以我们在想一想有没有什么其他更好的解法。
2.2 思路二——头尾双指针
因为题目说了数组是按照非递减顺序排列的,那么我们就要充分运用这个信息。而题目又要求两个数相加之和等于target,那么我们是不是就可以用两个指针来表示两个加数?
假设我们的两个指针一个指向数组的头命名为head,一个指向数组的尾命名为end,又因为数组是非递减的,是不是就相当于我的一个加数指向了最大值,一个加数指向了最小值。
那么我们是不是就可以尝试head+end=target ?如果相等,我们就返回,如果head+end > target,那么我们就可以把最大值 end变小,这样整体的和就会变小,再尝试相加。如果 head+end < target,那么就尝试把小的值 head变大,这样整体的和就会变大,再尝试相加。具体如下:

这样得到的head与end就是最终需要的结果了。
现在我们再来讨论一下为什么这样就行,因为总感觉没有经过证明的东西拿起来就不是那么的稳。用直观的表示来讲,我们的head与end分别代表了整个数组中的最小值与最大值,而因为head后有所有更大的值,end前有所有更小的值。
-
假设我们还是刚才示例的数组
numbers={2, 7, 11, 15},那么该numbers的所有可能的和假设为集合A,那么A={9, 13, 17, 18, 22, 26} -
所以假设head自始至终都不动,end不断前移,也就是我们能从当前和一直变到整个可能性集合A中最小的和也就是
9如下图所示:

-
而如果假设end不动,head不断后移,也就是我们能从当前和一直变到整个可能性集合A中最大的和也就是
26如下图所示:

现在我们再来看细一点:numbers的所有和的集合 A={9, 13, 17, 18, 22, 26},假设head还是指向头部,end还是指向尾部,下图第一行表示 end前移,而第二行表示head后移:

可以发现除了一个中间的和 18 其它的值都被覆盖了。而此时如果将head后移一位,再重复上述图示的步骤,肯定能获取到 18:

其实也就是表示我通过head与end相加,以及通过head后移和end前移,肯定可以遍历出整个numbers可能的和的集合A的所有元素,而我的target肯定在A中,因为题目说了 仅存在一个有效答案。
而换个解释就是说:我们的head和end相加的值,因为和target进行了比较,小了就变大,打了就变小,所以说就是不断向target收缩的过程,假设我们的 target=18:

通过小了就变大,大了就变小的原则,不断向target靠近,直到找到target。所以通过这种方法
-
第一能找到所有可能的和,不用担心缺了某一个和而导致找不到target。
-
第二我是通过不断向目标收缩的过程去找寻目标,而目标肯定在我的到的小了与大了的范围之内,拿上述例来说就是 17小了 和 22大了 这个【17,22】范围之内,而我是有小了就变大和大了就变小的原则,因此只能在17和22这个范围不断收缩,这样就能不断贴近目标直到找到目标。
思路二:更好的解释(引自Leetcode nettee)



(侵权请告知,立删)
3. 代码实现
3.1 思路一——暴力求解

3.2 思路二——头尾双指针

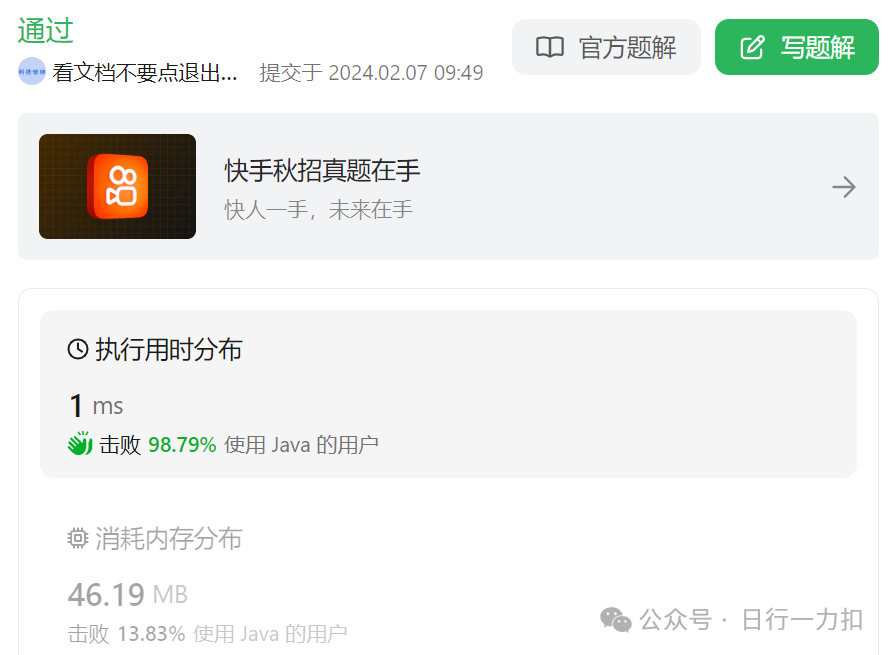
4. 运行结果
4.1 思路一——暴力求解

4.2 思路二——头尾双指针
5. 相关复杂度分析
5.1 思路一——暴力求解
-
时间复杂度:O(n^2),其中 n 是数组的长度。遍历数组的每个元素,每个元素还需要遍历其后面的元素。
-
空间复杂度:O(1)。
5.2 思路二——头尾双指针
-
时间复杂度:O(n),其中 n 是数组的长度。两个指针移动的总次数最多为 n 次。
-
空间复杂度:O(1)。