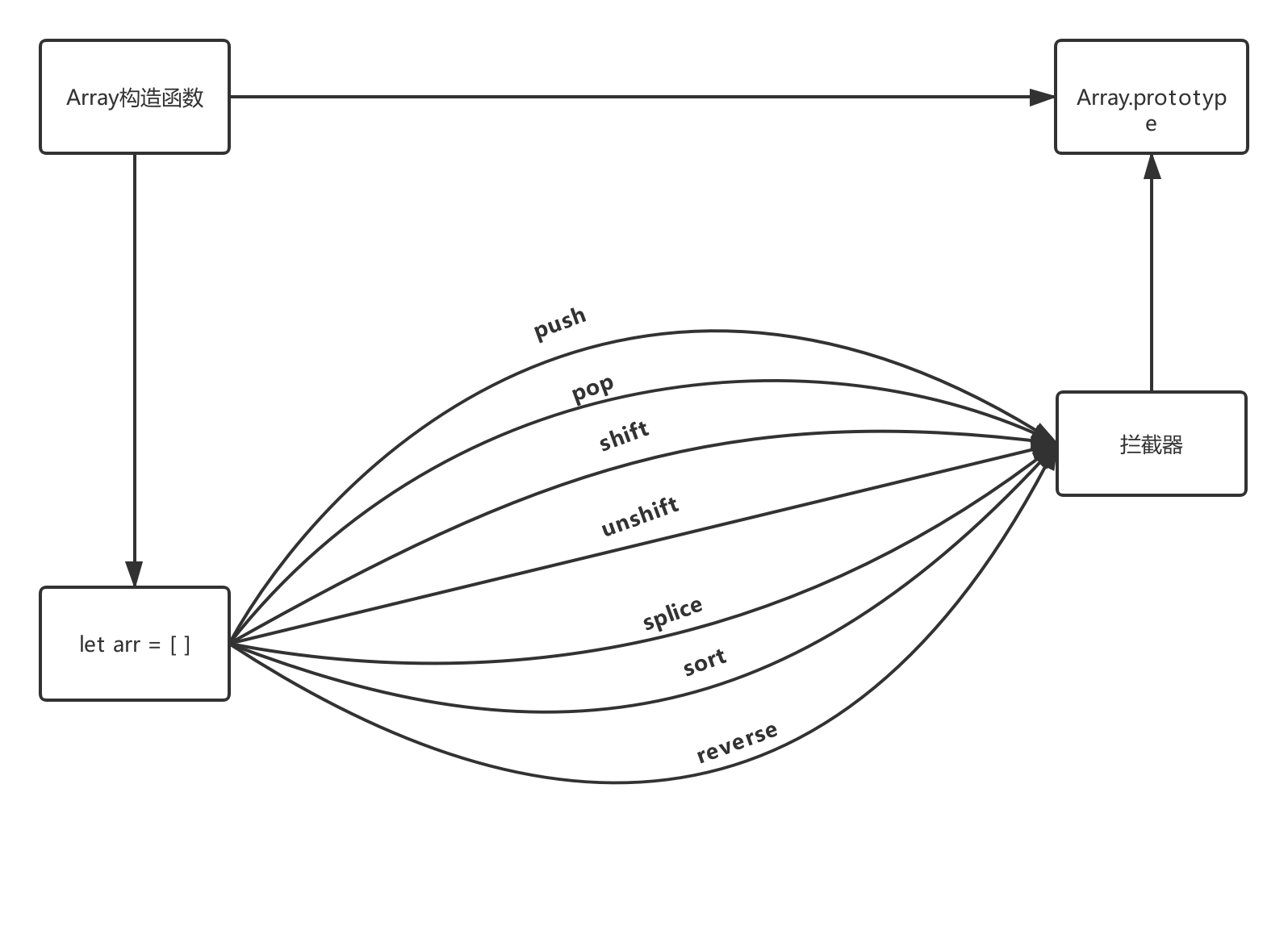
思路一：dfs深度优先搜索，然后取最小路径值，但是时间消耗较大，时间复杂度可能不满足，代码如下：

class Solution {
public:
    int res = 1000000;
    int rows,cols;
    int minPathSum(vector<vector<int>>& grid) {
        rows = grid.size();
        cols = grid[0].size();
        dfs(grid,0,0,0);
        return res;
    }
    void dfs(vector<vector<int>>& grid,int row,int col,int sum){
        sum += grid[row][col];
        if(row == rows-1 && col == cols-1){
            res = min(sum,res);
            return;
        }
        if(row < rows-1) dfs(grid,row+1,col,sum);
        if(col < cols-1) dfs(grid,row,col+1,sum);
    }
};

思路二：动态规划，记录每个节点的最小路径值，最后可得出最后一个节点的最小路径值

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int rows = grid.size();
        int cols = grid[0].size();
        vector<vector<int>> dp(rows,vector<int>(cols));
        //第一个节点为本身值
        dp[0][0] = grid[0][0];
        //第一行的最小路径值，因为只有一条路径
        for(int i = 1;i < cols;i++){
            dp[0][i] = dp[0][i-1] + grid[0][i];
        }
        //第一列的最小路径值，因为只有一条路径
        for(int i = 1;i < rows;i++){
            dp[i][0] = dp[i-1][0] + grid[i][0];
        }
        //其余的最小路径值
        for(int i = 1;i < rows;i++){
            for(int j = 1;j < cols;j++){
                //从左或者从右到达当前节点比较两者最小值，然后加上自身
                dp[i][j] = min(dp[i][j-1],dp[i-1][j]) + grid[i][j];
            }
        }
        //得出最后一个节点的最小路径值
        return dp[rows-1][cols-1];
    }
};