对板子的详细解释见：pecco:kmp

板子

void get_pmt(const string& p) {//求pmt数组
    for (int i = 1, j = 0;i < p.size();i++) {
        while (j && p[i] != p[j])j = pmt[j - 1];
        if (p[i] == p[j])j++;
        pmt[i] = j;
    }
}

void kmp(const string& s, const string& p) {//kmp算法
    for (int i = 0, j = 0;i < s.size();i++) {
        while (j && s[i] != p[j])j = pmt[j - 1];
        if (s[i] == p[j])j++;
        if (j == p.size()) {
            cout << i - j + 2 << '\n';
            j = pmt[j - 1];
        }
    }
}

注

pmt数组含义：截图来自peccp的文章kmp算法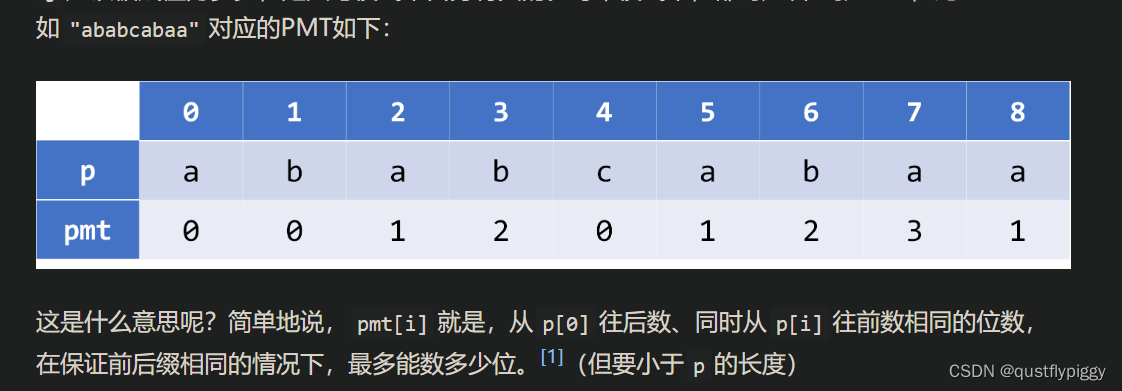

例题

洛谷p3375kmp模板

#include<bits/stdc++.h>

using namespace std;

const int M = 1e6 + 9;
int pmt[M];

void get_pmt(const string& p) {
    for (int i = 1, j = 0;i < p.size();i++) {
        while (j && p[i] != p[j])j = pmt[j - 1];
        if (p[i] == p[j])j++;
        pmt[i] = j;
    }
}

void kmp(const string& s, const string& p) {
    for (int i = 0, j = 0;i < s.size();i++) {
        while (j && s[i] != p[j])j = pmt[j - 1];
        if (s[i] == p[j])j++;
        if (j == p.size()) {
            cout << i - j + 2 << '\n';
            j = pmt[j - 1];
        }
    }
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    string s, p;cin >> s >> p;
    get_pmt(p);
    kmp(s, p);
    for (int i = 0;i < p.size();i++)cout << pmt[i] << ' ';
    return 0;
}