LeetCode 200：岛屿数量（图的简化版之网格结构上的BFS、DFS）

news2024/10/7 8:20:36

图的BFS和DFS

首先让我们回顾一下图的BFS和DFS遍历。可以看到这种BFS和DFS板子适用于图形状，或者说结构已经确定，即我们遍历的时候只需要从根节点从上往下遍历即可，不用考虑这个节点有几个叶子节点，是否会遍历到空节点等边界情况的问题。

public class Graph{
    public HashMap<Integer,Node>nodes;//点集，第一个参数是点的编号。和Node类中的value一致。不一定是Integer类型的，要看具体的题，有的题点编号为字母。
    public HashSet<Edge>edges;//边集

    public Graph(){
        nodes = new HashMap<>();
        edges = new HashSet<>();
    }
}

public class Node{
    public int value;//点的编号，不一定是Integer类型的，要看具体的题，有的题点编号为字母。
    public int in;//入度
    public int out;//出度
    public ArrayList<Node>nexts;//出去的边直接相连的邻居。
    public ArrayList<Edge>edges//出去的边

    public Node(int value){
        this.value=value;
        in = 0;
        out = 0;
        nexts = new ArrayList<>();
        edges = new ArrayList<>();
    }
}

public class Edge{
    public int weight;//边上权重
    public Node from;
    public Node to;

    public Edge(int weight,Node from,Node to){
        this.weight=weight;
        this.from=from;
        this.to=to;
    }
}

public static void bfs(Node node){
    if(node==null) return;
    Queue<Node> queue = new LinkedList<>();
    HashSet<Node> set = new HashSet<>();
    queue.add(node);
    set.add(node);
    while(!queue.isEmpty()){
        Node cur = queue.poll();
        /*  具体的处理逻辑
            （宽搜一般是结点入队列后再处理）
        */
        for(Node next: cur.nexts){
            if(!set.contains(next)){//如果set中没有，那么说明这个next结点没有被访问过
            queue.add(next);//扔到队列里
            set.add(next);//并且标记访问
            }
        }
    }
}

public static void dfs(Node node){
    if(node==null) return;
    Stack<Node> stack = new Stack<>();
    HashSet<Node> set = new HashSet<>();
    stack.add(node);
    set.add(node);
    /*具体的处理逻辑（深搜一般是结点入栈前就进行处理）*/
    while(!stack.isEmpty()){
        Node cur = stack.pop();
        for(Node next:cur.nexts){
            if(!set.contains(next)){
                stack.push(cur);//在这里需要把cur和next两个结点同时入栈是因为
                stack.push(next);//想在栈里保持深度搜索的路径。这次搜索相比于上一次搜索，在栈中就多了一个next结点。
                set.add(cur);
                set.add(next);
                /*具体的处理逻辑 */
                break;//之所以立马break是因为深搜每次只走一步，不像宽搜每次走一层。
            }
        }
    }
}

网格结构的dfs、bfs（岛屿问题）

网格结构

但是网格结构的题不一样，一般这种题不会给出图的结构或者形状，而且不会给出根节点的具体位置，那么我们由网格结构构造图结构也比较麻烦。
首先让我们了解一下什么是网格结构。以下内容来自于力扣用户：nettee

网格结构是由 m×n个小方格组成一个网格，每个小方格与其上下左右四个方格认为是相邻的，要在这样的网格上进行某种搜索。
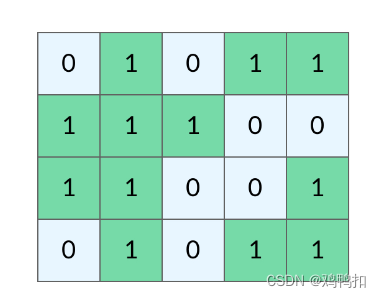
在这里插入图片描述
网格结构要比二叉树结构稍微复杂一些，它其实是一种简化版的图结构。

网格结构的dfs

要写好网格上的 DFS 遍历，我们首先要理解二叉树上的 DFS 遍历方法，再类比写出网格结构上的 DFS 遍历。我们写的二叉树 DFS 遍历一般是这样的：

void traverse(TreeNode root) {
    // 判断边界情况
    if (root == null) {
        return;
    }
    // 访问两个相邻结点：左子结点、右子结点
    traverse(root.left);
    traverse(root.right);
}

可以看到，二叉树的 DFS 有两个要素：「访问相邻结点」和「判断边界情况」。
对于网格上的 DFS，我们完全可以参考二叉树的 DFS，写出网格 DFS 的两个要素：

首先，网格结构中的格子有多少相邻结点？答案是上下左右四个。对于格子 (r, c) 来说（r 和 c 分别代表行坐标和列坐标），四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)。换句话说，网格结构是「四叉」的。
在这里插入图片描述其次，网格 DFS 中的边界情况是什么？就是超出网格m*n的范围或者遍历到已经遍历过的节点胡总和遍历到不能遍历的点（岛屿问题中的海洋格子）。
这样，我们得到了网格 DFS 遍历的框架代码：

板子

void dfs(int[][] grid, int r, int c) {
    // 判断边界情况
    // 如果坐标 (r, c) 超出了网格范围，直接返回
    if (!inArea(grid, r, c)) return;
    if(vis[r][c]==true||grid[r][c]==0) return;
    // 访问上、下、左、右四个相邻结点
    dfs(grid, r - 1, c);
    dfs(grid, r + 1, c);
    dfs(grid, r, c - 1);
    dfs(grid, r, c + 1);
}

// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
    return 0 <= r && r < grid.length 
        	&& 0 <= c && c < grid[0].length;
}

其中的vis[r][c]==true的判断可以试不同的题而作改动，像是一般有固定数值的网格问题，譬如0表示海洋，1表示陆地的岛屿问题，我们就可以每遍历一个格子后修改其值为2，表示这个是已经遍历过的陆地格子。然后直接判断if(grid[r][c]!=1)这样就不需要额外的一个vis数组去存储遍历信息了。

LC 200题解

对于LC 200该题而言，代码就是

public int numIslands(char[][] grid) {
        int num = 0;
        for(int r=0;r<grid.length;r++){
            for(int c=0;c<grid[0].length;c++){
                if(grid[r][c]=='1'){//外层的话我需要找到所有陆地格子，而不只是一个陆地格子
                //因为可能有多个不连通子图
                    dfs(grid,r,c);
                    num++;
                }
            }
        }
        return num;
    }
    public void dfs(char[][] grid, int r,int c){
        if(!ifCouldVis(grid,r,c)) return;
        grid[r][c]='2';
        dfs(grid,r+1,c);
        dfs(grid,r,c+1);
        dfs(grid,r-1,c);
        dfs(grid,r,c-1);
    }

    public boolean ifCouldVis(char[][] grid, int r,int c){
        return r>=0&&c>=0&&r<grid.length&&c<grid[0].length&&grid[r][c]=='1';
    }