树状数组

lowbit

在学习树状数组之前，我们需要了解lowbit操作，这是一种位运算操作，用于计算出数字的二进制表达中的最低位的1以及后面所有的0。
写法很简单：

int lowbit（int x）｛return x ＆-x；｝

这是利用了计算机存储整数的特性来写的，在计算机中整数都使用补码进行存储，原理不做深究，记住怎么写即可。

树状数组基础

树状数组是一种可以“动态求区间和”的树形数据结构，但并没有真正地构造出边来，所以是“树状”的。
基础的树状数组可以实现对区间和的单点修改和区间查询时间复杂度均为O（logn）.
树状数组所需的东西非常简单，就一个数组int［N］，大小和我们所需要维护的数组大小一样即可

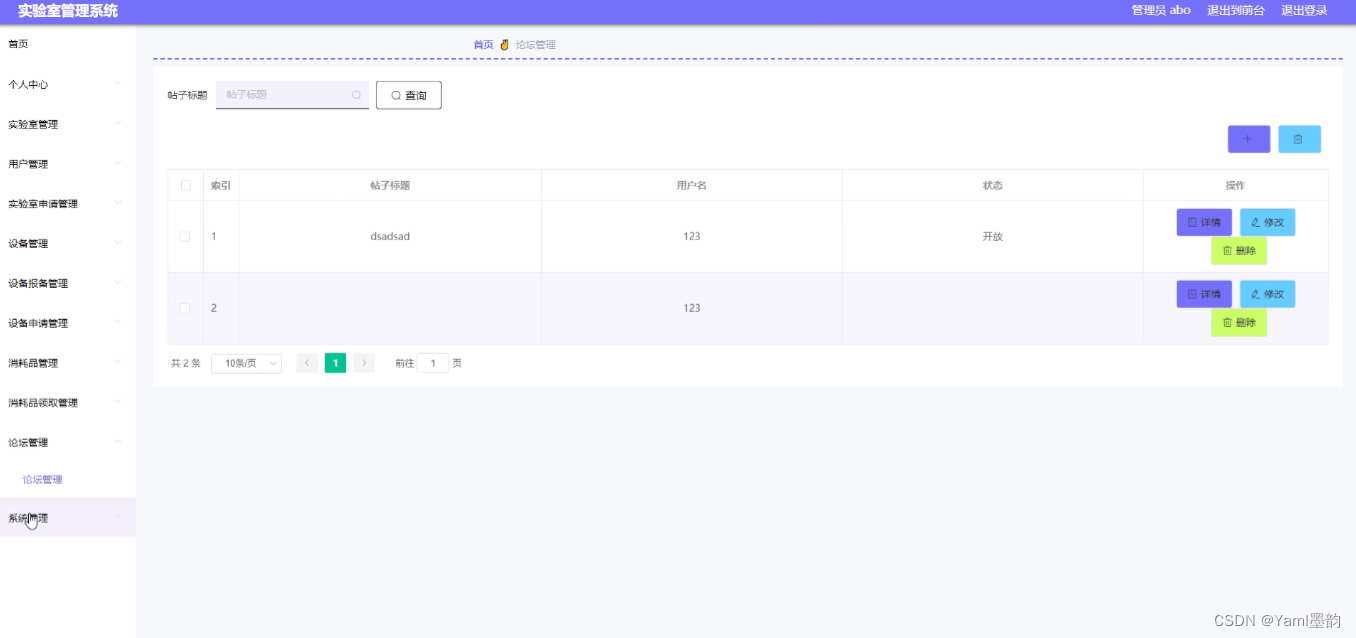
先看下树状数组的结构：
其中t［i］存储a［］数组中一段区间的和，具体区间
怎么算呢？
我们定义是让t［i］存储以i结尾且区间大小为
lowbit（i）的区间的和。
$$\sum _{j=i-\text{lowbit}(i)+1}^i{a}_i$$
我习惯于叫［i-lowbit（i）+1，i］为i的管辖区间。

怎么进行单点修改？
举个例子，假如我要修改a［3］，让他加上x，在右边这个图中我们可以看出，我们应该修改
t3，t4和t8共3个节点。因为这三个节点的管辖区间内都包含3这个节点
但是我们如何从3开始，去找到3，4，8呢？
只需要进行+lowbit操作即可（二进制性质）。
3 + lowbit（3） = 4
4 + lowbit（4） = 8
…

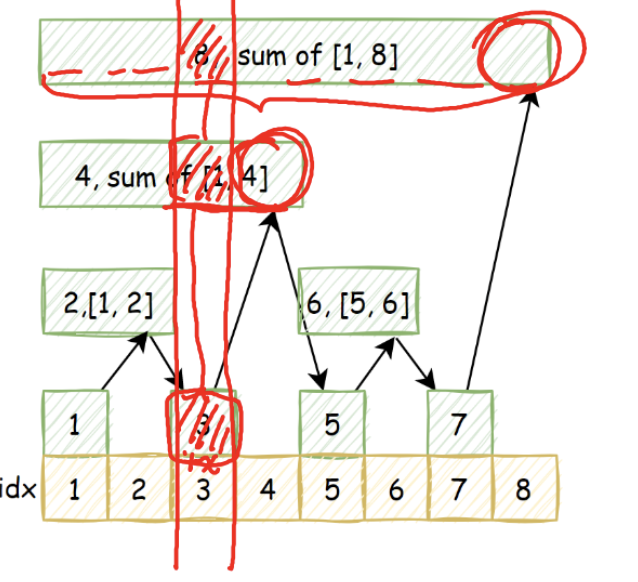
怎么进行区间查询？
第一步我们将其拆为两个区间的差，举个例子，我们要查询区间［3，7］的和，就要拆分为sum［1，7］ －sum［1，2］，回想一下前缀和的写法~
现在问题变为如何查询［1，k］的和？
假如我们要求sum［1，7］，我们从右图可以知道结果为t［7］+t［6］+t［4］，这是怎么得到的呢？
通过－lowbit可：
7 - lowbit（7） = 6
6 - lowbit（6）= 4

于是我们可以直接得到树状数组最重要的两个函数update()和getprefix().
大功告成！

// 给 a[k] 增加 x
void update(int k, int x) {
    for (int i = k; i <= n; i += lowbit(i)) {
        t[i] += x;
    }
}

// 返回区间 [1, k] 的和
int getprefix(int k) {
    int res = 0;
    for (int i = k; i > 0; i -= lowbit(i)) {
        res += t[i];
    }
    return res;
}

殷老师排队

思路：将式子转化，用树状数组模拟题意

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+9;
using ll = long long ;
ll a[N],t[N],n,m;
int lowbit(int x){
    return x&-x;
}

void update(int k,int x){
    a[k] += x;
    for(int i=k;i<=n;i+=lowbit(i)){
        t[i] +=x;
    }
}

ll getPrefix(int k){
    ll res =0;
    for(int i=k;i>0;i-=lowbit(i)){
        res+=t[i];
    }
    return res;
}

ll getSum(int l,int r){
    return getPrefix(r) - getPrefix(l-1);
}
 
int b(int i){
    return (2*i - n - 1)*a[i] - getSum(1, i-1) + getSum(i+1, n);
}

int main( ){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        int x;cin>>x;
        update(i,x);
    }
    while(m--){
        int op;cin>>op;
        if(op==1){
            int k,b;cin>>k>>b;
            update(k, -a[k]+b);
        }else{
            int i;cin>>i;
            cout<<b(i)<<'\n';
        }
    }
    return 0;
}