01背包理论基础
学习资料:代码随想录 (programmercarl.com)
相关链接:题目页面 (kamacoder.com)
背包题目分类
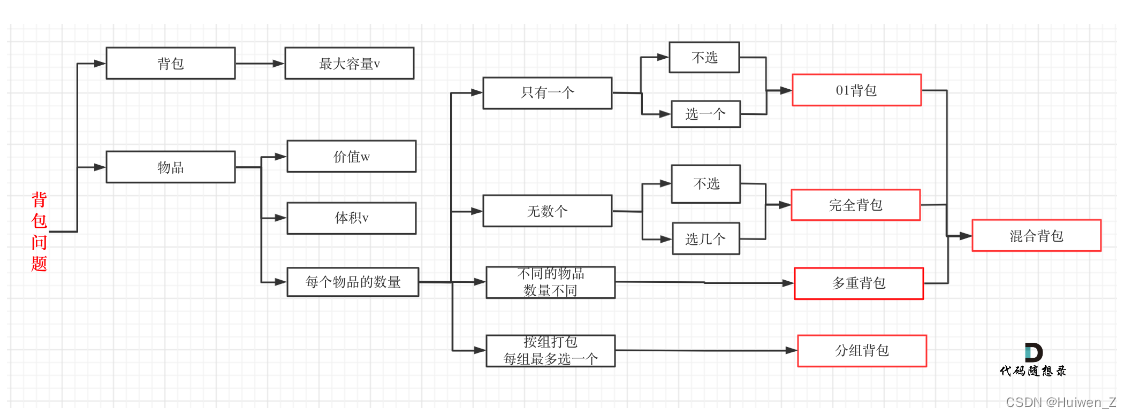
01背包定义
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
解法
暴力解法
每种物品有两种状态:取或不取,因此可以用回溯法搜索出所有组合,选出价值最大的方案,时间复杂度为o(2^n)。
动态规划
举例:背包重量为4,物品为:
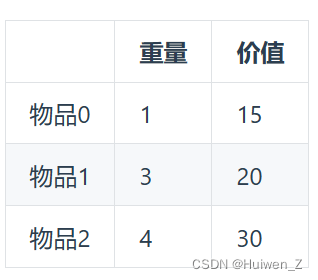
1. dp[i][j]定义
当前背包容量为j时, 从下标为[0, i]的物体中任意取,放到背包中,的最大价值。
示意图如下:
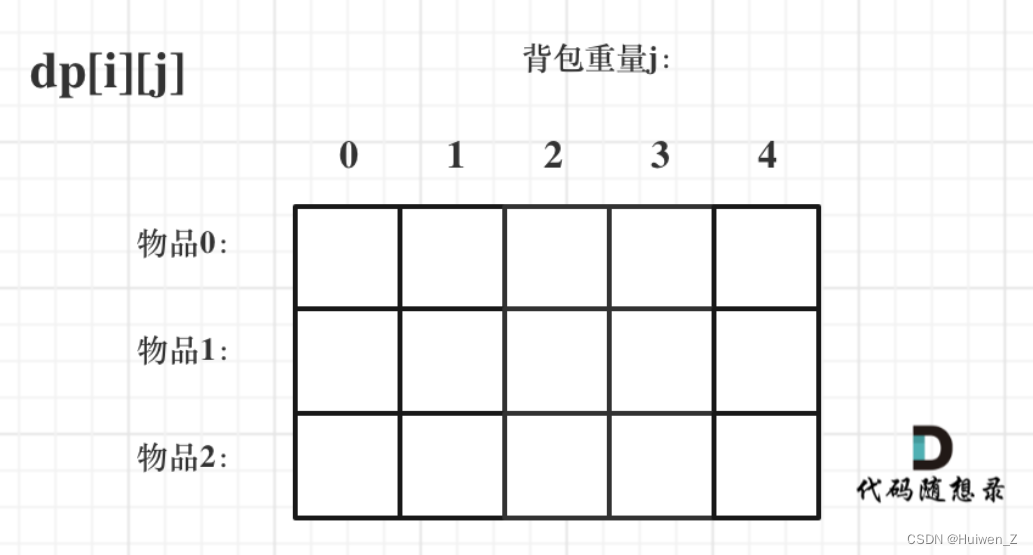
2.递推公式
dp[i][j]可以从两个方向得到:
- 放物品i: 由dp[i - 1][j - weight[i]]推出,即不放物品i时,容量为[j - weight[i]的背包(要给物品i流出放的重量)时的最大价值加上物品i的价值。
- 不放物品i:由dp[i-1][j]推出,即容量为j,不放物品i时的最大价值。
递推公式为: dp[i][j] = max(dp[i-1][j], dp[i-1][j - weight[i]] + value[j])
3. 初始条件
- 当背包容量为0时,那么不管从哪几个物体中选,最大价值总为0.
- 当i为0时,即只能选择放入物品0或不放入物品0,想得到最大价值,肯定选择物品0最好, 但如果物品0重量大于背包容量时就无法放入,最大价值为0。
4. 遍历顺序
dp[i][j]由[i][j]位置的上方或者左上方得到,可以先遍历物品,也可以先遍历容量,我选择前者。具体步骤如下:
首先从dp[1][1]开始计算,当前物品1的重量(3)超过了背包总容量(1),所以无论之前的物品(这里指物品0)有没有放入背包,物品1都不可能放进去,所以背包的最大价值和在当前容量下放入物品1前的最大价值相同,即dp[1][1] = dp[0][1] = 15。dp[1][2]同理。
当背包扩容到3(即j = 3)时,直观来看,我们可以选择放入物品1,如果放入,就不能同时放入物品0,那么价值为20,如果不放物品1,可能的最大价值为只放物品0的价值,即15,因为20>15, 所以dp[1][3] = 20。把上述想法抽象总结如下:
容量大于物品1的容量,说明可以放入物品1。如果放入物品1,那留给前面的物体(这里指物品0)的容量只有j-wright[j](这里为0),所以前面物体能创造的最大价值为dp[i-1][j-weight[j]], 加上物品j后的价值为dp[i - 1][j - weight[j]] + value[i], 如果不放入物品1,那就和之前的情况一样,即dp[i-1][j]。取这两种情况价值大的,即max(dp[i - 1][j - weight[j]] + value[i], dp[i-1][j])。
5. 举例推导dp数组
在纸上举例,能写出下面的数组。
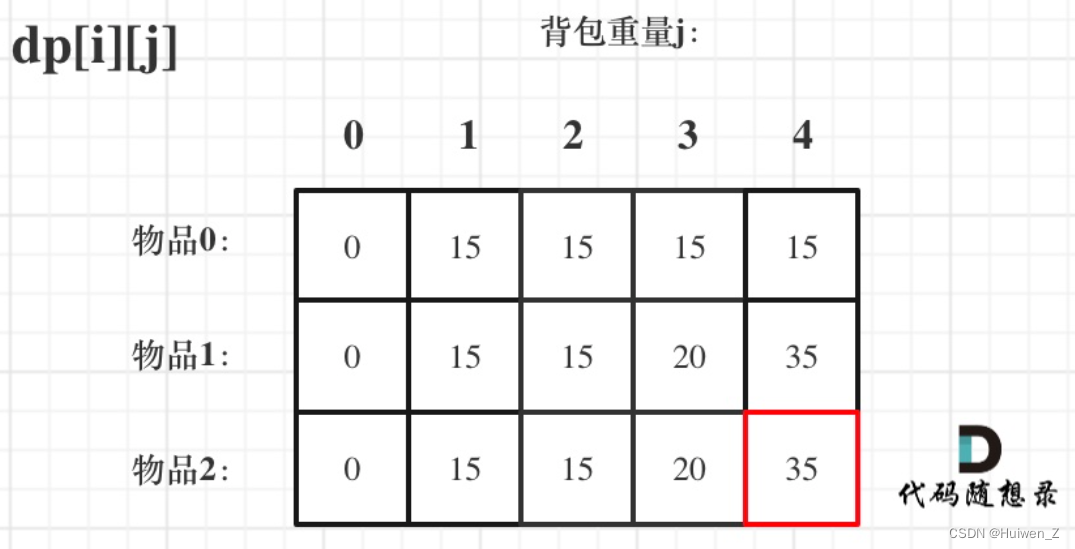
代码实现
在ACM模式下,Python的输入模式基础语句为下:
# 读取一个整数
n = int(input())
# 一行里有n个整数, 表示数据
a = list(map(int, input(),split()))
# 一行里面有两个整数
n, m = map(int, input().split())
# 如果有多行数据,则按照每行的顺序依次执行上述对应指令
objNum, bagWeight = map(int, input().split())
weight = [int(i) for i in input().split()]
value = [int(i) for i in input().split()]
dp = [[0]*(bagWeight+1) for i in range(objNum)]
for j in range(bagWeight+1):
if j >= weight[0]:
dp[0][j] = value[0]
for i in range(1, objNum): # 遍历
for j in range(1, bagWeight+1):
if weight[i] > j:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j], dp[i-1][j - weight[i]] + value[i])
print(dp[objNum - 1][bagWeight])