深度学习图像分类相关概念简析+个人举例3（CNN相关补充，附详细举例代码1）

【1】激活函数（Activation Function）：在深度学习（CNN）中，激活函数用于引入非线性性质，帮助模型学习复杂的关系。常见的激活函数有ReLU、Sigmoid和Tanh等。

（1）ReLU激活函数：ReLU函数将负输入值变为零，保留正输入值不变。

公式为 $f(x) = max(0, x)$

（2）Sigmoid激活函数：Sigmoid函数将任意实数映射到0到1之间。

公式为 $f(x) = 1 / (1 + exp(-x))$

（3）Tanh激活函数：Tanh函数将任意实数映射到-1到1之间。

公式为 $f(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x))$

这些激活函数可以作为CNN模型中的非线性变换函数，用于增加网络的表达能力。

【2】批归一化（Batch Normalization）：是一种用于加速深度神经网络训练的技术，通过对每一层的输入进行标准化，使得模型更加稳定和收敛更快。

步骤：

选择一个归一化的范围，一般是[0,1]或[-1,1]。
例如，我们选择[0,1]作为范围，然后找到数据集的最小值（min）和最大值（max）。
对于每个数据点，使用以下公式计算归一化后的值： normalized_value = (data_point - min) / (max - min)【（当前数据点-最小值点）/（最大-最小）】

【3】损失函数（Loss Function）：用于衡量模型预测结果与真实标签之间的差异。在图像分类任务中，常用的损失函数有交叉熵损失函数。

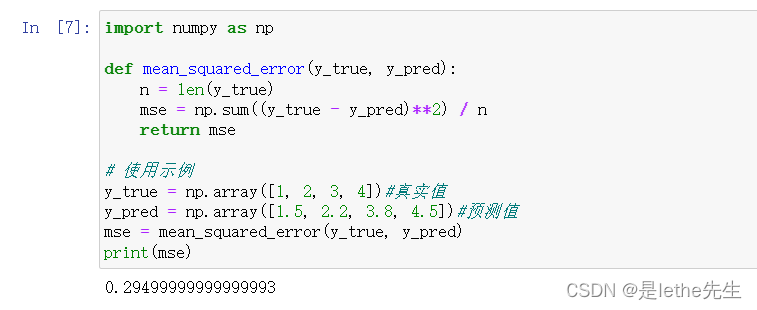
（1）均方误差（Mean Squared Error, MSE）：均方误差是预测值与真实值之间差距的平方的平均值。

公式： $MSE = (1/n) * Σ(y_true - y_pred)^2$

其中，n为样本数量，y_true为真实值，y_pred为模型预测值，Σ表示对所有样本求和。

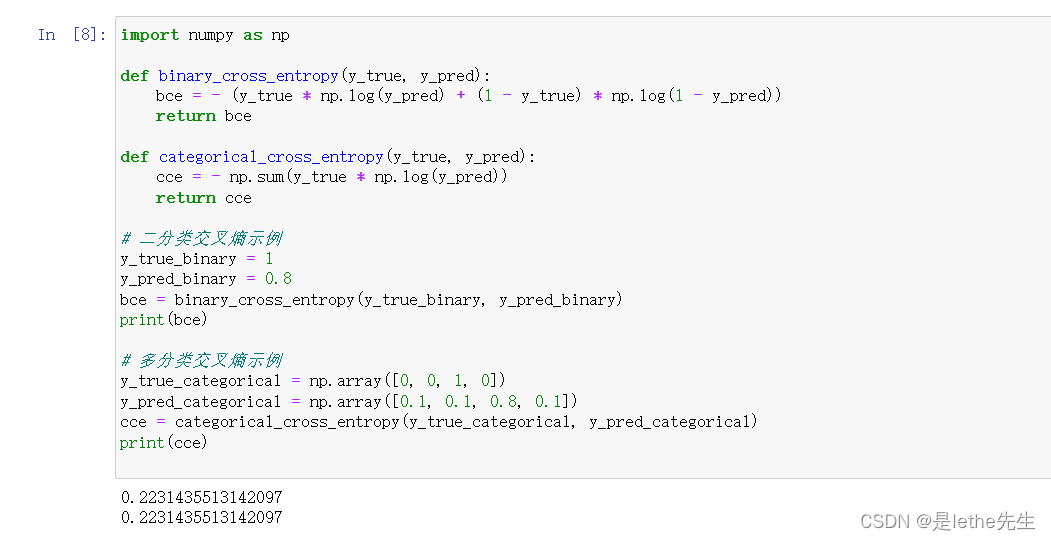
（2）交叉熵（Cross Entropy）：交叉熵是一种衡量概率分布之间差异的函数，用于多分类问题的损失函数。【用于衡量两个概率分布之间差异】

公式： $Binary Cross Entropy = - (y_true * log(y_pred) + (1 - y_true) * log(1 - y_pred))$

其中，y_true为真实标签（取值为0或1），y_pred为模型预测的概率值（范围在0到1之间），log为自然对数函数。

假设有一个二分类问题，有一个样本的真实标签为1，模型预测的概率为0.8。代入真实标签y_true=1和预测概率y_pred=0.8，就可以计算二分类交叉熵的值：Binary Cross Entropy = - (1 * log(0.8) + (1 - 1) * log(1 - 0.8)) = - (1 * log(0.8) + 0 * log(0.2)) = - log(0.8) ≈ 0.223。交叉熵值越小，表示模型的预测结果越接近真实情况。

【4】优化算法（Optimization Algorithm）：用于更新模型参数以最小化损失函数的算法。常见的优化算法有随机梯度下降（SGD）、Adam、Adagrad等。

在机器学习和深度学习中，模型往往具有大量的参数，通过优化算法可以自动调整这些参数，使模型能够更好地拟合训练数据，并在未见过的新数据上具有更好的泛化能力。优化算法的目标是最小化损失函数，从而提高模型的预测准确性和性能。

拟合是指通过拟合函数曲线来逼近已知数据点的过程。

【0】最小二乘法

最小二乘法是一种用于拟合数据的数学方法。它的基本思想是找到一条曲线或者函数，使得该曲线与给定的数据点之间的距离最小。

下面举一个简单的例子来演示最小二乘法的过程：

假设有一组数据点(1, 2)，(2, 3)，(3, 4)，(4, 5)，(5, 6)，我们希望通过最小二乘法找到一条直线来拟合这些数据点。

第一步是选择拟合函数的形式。在这个例子中，我们选择一条直线作为拟合函数，即y = ax + b。其中，a是直线的斜率，b是直线的截距。
第二步是建立最小二乘拟合的目标函数。最小二乘拟合的目标是使得实际数据点和拟合函数之间的距离最小。通常，这个距离可以用误差的平方和来表示。即： $E(a, b) = Σ(yi - (axi + b))^2$ ，其中(xi, yi)表示第i个数据点。
第三步是求解目标函数的最小值。为了找到目标函数的最小值，我们需要对目标函数进行求导，并令导数等于零。这样我们就可以得到方程组： $∂E/∂a = 0 ∂E/∂b = 0$ 。将目标函数和其导数进行展开和化简，可以得到如下的方程组 $Σ(xi^2)a + Σxi b = Σ(xi yi) Σ(xi)a + nb = Σyi$ ，其中，n表示数据点的个数。
第四步是解方程组。通过解方程组，我们可以得到最小二乘拟合的斜率a和截距b的数值。这样就得到了拟合函数y = ax + b。在这个例子中，我们可以计算得到斜率a为1，截距b为1。因此，最小二乘拟合的直线函数为y = x + 1。最后，我们可以将最小二乘拟合的直线绘制在原始数据点上，以观察拟合的效果。

【1】线性拟合

举个简单例子，假设有以下数据点：

x = [1, 2, 3, 4, 5]
y = [3, 5, 7, 9, 11]

我们可以假设这些数据点满足线性关系，即 y = mx + c，其中 m 是斜率， c 是截距。我们的目标是找到最佳的 m 和 c 的值，使得拟合函数能够最好地逼近这些数据点。在这个例子中，我们可以使用最小二乘法进行拟合。最小二乘法的目标是最小化实际观测值与拟合函数预测值之间的平方差。具体来说，我们需要找到 m 和 c 的值，使得误差的平方和最小。通过求解最小二乘问题，我们可以得到最佳的 m 和 c 的值。在这个例子中，最佳的拟合函数为 y = 2x + 1。当我们把这个拟合函数应用于新的 x 值时，可以得到预测的 y 值，从而实现对未知数据的预测。

详细的该过程如下：

计算数据点的个数 n。
计算 x 和 y 的平均值：mean_x = (1+2+3+4+5)/5 = 3，mean_y = (3+5+7+9+11)/5 = 7。
计算 x 和 y 的差值：dx = [1-3, 2-3, 3-3, 4-3, 5-3] = [-2, -1, 0, 1, 2]，dy = [3-7, 5-7, 7-7, 9-7, 11-7] = [-4, -2, 0, 2, 4]。
计算 dx 和 dy 的乘积之和：sum_dx_dy = (-2)(-4) + (-1)(-2) + 00 + 12 + 2*4 = 14。
计算 dx 的平方和：sum_dx_squared = (-2)^2 + (-1)^2 + 0^2 + 1^2 + 2^2 = 10。
计算斜率 m：m = sum_dx_dy / sum_dx_squared = 14 / 10 = 1.4。
计算截距 c：c = mean_y - m * mean_x = 7 - 1.4 * 3 = 2.8。

线性拟合的结果为 y = 1.4x + 2.8。通过这个拟合函数，我们可以预测新的 x 值获得对应的 y 值。

【2】多项式拟合

假设有以下数据点：x = [1, 2, 3, 4, 5] y = [1.2, 3.5, 9.1, 16.9, 28.3]

我们可以假设这些数据点满足二次多项式关系，即 y = ax^2 + bx + c，其中 a、b、c 是多项式的系数。我们的目标是找到最佳的 a、b、c 的值，使得拟合函数能够最好地逼近这些数据点。多项式拟合的计算过程可以通过最小二乘法来求解最佳的拟合参数。具体而言，我们需要找到 a、b、c 的值，使得误差的平方和最小。

计算步骤如下：

假设初始的参数值为 a = 1，b = 1，c = 1。
对于每个数据点 (xi, yi)，计算拟合函数的预测值 y_pred = axi^2 + bxi + c。
计算每个数据点的误差：error = yi - y_pred。
计算误差的平方和：sum_squared_error = (error1)^2 + (error2)^2 + ... + (errorn)^2。
根据最小二乘法的原理，我们需要找到能够最小化 sum_squared_error 的 a、b、c 的值。
使用优化算法，如梯度下降法或牛顿法，调整参数 a、b、c 的值，重复步骤 2-5，直到找到最佳的拟合参数。

通过多项式拟合计算，最终可以得到最佳的 a、b、c 的值，从而得到多项式拟合的函数表达式。需要注意的是，多项式阶数的选择也会影响拟合效果，过高的阶数可能会导致过拟合，而过低的阶数可能会导致欠拟合。因此，在实际应用中，需要进行模型选择和评估来找到最合适的多项式阶数。

【3】非线性拟合

假设有以下数据点：x = [1, 2, 3, 4, 5] y = [3.2, 7.5, 18.1, 39.9, 85.3]

我们可以假设这些数据点满足指数关系，即 $y = ae^(bx)$ ，其中 a 是指数函数的缩放因子， b 是指数函数的指数。我们的目标是找到最佳的 a 和 b 的值，使得拟合函数能够最好地逼近这些数据点。非线性拟合通常也使用最小二乘法来求解最佳的拟合参数。具体而言，我们需要找到 a 和 b 的值，使得误差的平方和最小。

计算步骤如下：

假设初始的参数值为 a = 1 和 b = 1。
对于每个数据点 (xi, yi)，计算拟合函数的预测值 y_pred = ae^(bx)。
计算每个数据点的误差：error = yi - y_pred。
计算误差的平方和：sum_squared_error = (error1)^2 + (error2)^2 + ... + (errorn)^2。
根据最小二乘法的原理，我们需要找到能够最小化 sum_squared_error 的 a 和 b 的值。
使用优化算法，如梯度下降法或牛顿法，调整参数 a 和 b 的值，重复步骤 2-5，直到找到最佳的拟合参数。

【5】数据增强（Data Augmentation）：为了增加训练数据的多样性和数量，可以通过一系列的图像增强操作，如翻转、旋转、缩放等，生成新的训练样本。

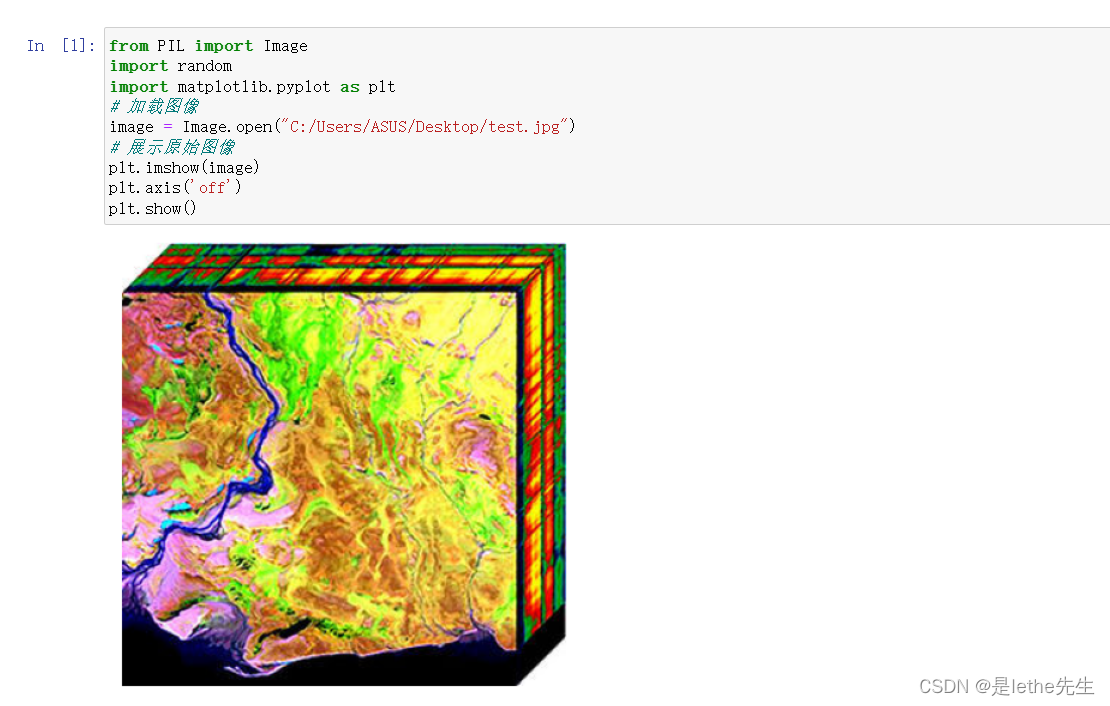
这里随便搜一张图当例子吧，就下面这张，我随便搜的，你们想用别的也可以~我随便搜了一张.jpeg文件，大小是300×300的，命名为test保存在桌面（我习惯了，想存别的盘也可以滴~）,然后先导入思密达~

【1】随机水平翻转：将图像水平翻转，即左右翻转。这个操作可以增加训练集的多样性，尤其在处理镜像对称的物体时很有用。

def random_flip(image):
    flipped_image = image.transpose(Image.FLIP_LEFT_RIGHT)
    return flipped_image

【2】随机垂直翻转：将图像垂直翻转，即上下翻转。类似于水平翻转，垂直翻转也可以增加数据集的多样性。

def random_flip(image):
    flip = random.choice([Image.FLIP_LEFT_RIGHT, Image.FLIP_TOP_BOTTOM])
    flipped_image = image.transpose(flip)
    return flipped_image

【3】随机裁剪：随机选择图像的一部分进行裁剪。这个操作能够帮助模型学习不同部分之间的关系，同时也能够减轻过拟合。

# 随机裁剪
def random_crop(image, size):
    width, height = image.size
    crop_width, crop_height = size
    
    x = random.randint(0, width - crop_width)
    y = random.randint(0, height - crop_height)
    
    cropped_image = image.crop((x, y, x+crop_width, y+crop_height))
    return cropped_image

# 定义裁剪后的尺寸
crop_size = (200, 200)

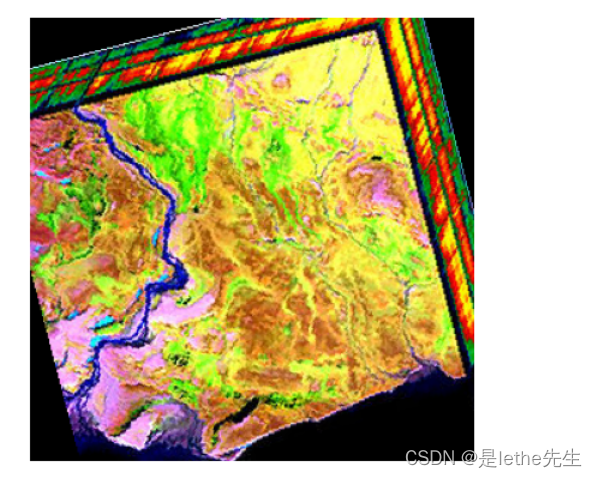
【4】随机旋转：随机旋转图像一定的角度。这个操作可以模拟实际场景中的不同角度拍摄，增加模型的鲁棒性。

# 随机旋转
def random_rotation(image, angle_range):
    angle = random.uniform(-angle_range, angle_range)
    rotated_image = image.rotate(angle)
    return rotated_image

# 定义旋转角度范围
angle_range = 30

【5】随机缩放：随机改变图像的尺寸，可以放大或缩小图像。这个操作可以模拟不同距离下的拍摄，增加模型对尺度变化的适应能力。

# 随机缩放
def random_scaling(image, scale_range):
    scale = random.uniform(scale_range[0], scale_range[1])
    width, height = image.size
    new_width = int(width * scale)
    new_height = int(height * scale)
    scaled_image = image.resize((new_width, new_height))
    return scaled_image

# 定义缩放范围
scale_range = (1.0, 2.0)

【7】随机噪声添加：向图像中添加随机噪声，可以增加模型对噪声的鲁棒性。

# 随机噪声添加
def random_noise(image, noise_level):
    width, height = image.size
    pixels = np.array(image)
    noise = np.random.randint(-noise_level, noise_level, (height, width, 3))
    noisy_image = np.clip(pixels + noise, 0, 255).astype(np.uint8)
    noisy_image = Image.fromarray(noisy_image)
    return noisy_image

# 定义噪声级别
noise_level = 30

【6】随机亮度调整：随机改变图像的亮度。这个操作可以增加模型对不同光照条件下的适应性。

# 随机亮度调整
def random_brightness(image, brightness_level):
    pixels = np.array(image)
    brightness = np.random.randint(-brightness_level, brightness_level)
    brightened_image = np.clip(pixels + brightness, 0, 255).astype(np.uint8)
    brightened_image = Image.fromarray(brightened_image)
    return brightened_image

# 定义亮度调整级别
brightness_level = 50

【8】随机颜色调整：随机调整图像的颜色，如亮度、对比度、饱和度等。这个操作可以增加模型对不同颜色和光照条件的适应性。

# 随机颜色调整
def random_color(image, color_level):
    pixels = np.array(image)
    color_adjustment = np.random.randint(-color_level, color_level, size=3)
    adjusted_image = np.clip(pixels + color_adjustment, 0, 255).astype(np.uint8)
    adjusted_image = Image.fromarray(adjusted_image)
    return adjusted_image

# 定义颜色调整级别
color_level = 50