1. 前置知识
1.1 YOLO 算法的基本思想

首先通过特征提取网络对输入图像提取特征,得到一定大小的特征图,比如 13x13(相当于416x416 图片大小),然后将输入图像分成 13x13 个 grid cells:
- YOLOv3/v4:如果 GT 中某个目标的中心坐标落在哪个 grid cell 中,那么就由该 grid cell 来预测该目标。每个 grid cell 都会预测 3 个不同尺度的边界框。
- YOLOv5:不同于 YOLOv3/v4,其 GT 可以跨层预测,即有些 bbox(anchors)在多个预测层都算正样本,匹配数的正样本范围可以是 3-9 个。
预测得到的输出特征图有两个维度是提取到的特征的维度,比如 13x13,还有一个维度(深度)是 Bx(5+C),其中:
- B 表示每个 grid cell 预测的边界框的数量(YOLOv3/v4中是 3 个)
- C 表示边界框的类别数(没有背景类,所以对于 VOC 数据集是 20)
- 5 表示 4 个坐标信息和一个目标性得分(objectness score)
1.2 损失函数
- Classification Loss:
- 用于衡量模型对目标的分类准确性。
- 计算方式通常使用交叉熵损失函数,该函数衡量模型的分类输出与实际类别之间的差异。
- 对于 YOLOv5,每个目标都有一个对应的类别,分类损失量化了模型对每个目标类别的分类准确性。
- Localization Loss:定位损失(预测边界框与 GT 之间的误差)
- 用于衡量模型对目标位置的预测准确性。
- YOLOv5 中采用的是均方差(Mean Squared Error,MSE)损失函数,衡量模型对目标边界框坐标的回归预测与实际边界框之间的差异。
- 定位损失关注模型对目标位置的精确度,希望模型能够准确地定位目标的边界框。
- Confidence Loss:置信度损失(框的目标性 <=> Objectness of the box)
- 用于衡量模型对目标存在与否的预测准确性。
- YOLOv5 中采用的是二元交叉熵损失函数,该函数衡量模型对目标存在概率的预测与实际目标存在的二元标签之间的差异。
- 置信度损失考虑了模型对每个边界框的目标置信度以及是否包含目标的预测。该损失鼓励模型提高对包含目标的边界框的预测概率,同时减小对不包含目标的边界框的预测概率。
总的损失函数:
L o s s = α × C l a s s i f i c a t i o n L o s s + β × L o c a l i z a t i o n L o s s + γ × C o n f i d e n c e L o s s \rm Loss = \alpha \times Classification Loss + \beta \times Localization Loss + \gamma \times Confidence Loss Loss=α×ClassificationLoss+β×LocalizationLoss+γ×ConfidenceLoss
1.3 PyTorch2ONNX
Netron 对 .pt 格式的兼容性不好,直接打卡无法显示整个网络。因此我们可以使用 YOLOv5 中的 models/export.py 脚本将 .pt 权重转换为 .onnx 格式,再使用 Netron 打开就可以完整地查看 YOLOv5 的整体架构了。
python export.py \
--weights weights/yolov5s.pt \
--imgsz 640 \
--batch-size 1 \
--device cpu \
--simplify \
--include onnx
💡 详细可选参数见
export.py文件
1.4 YOLOv5 模型结构图

图片来源:霹雳吧啦Wz
2. 配置文件
在 models 中的 .yaml 文件是模型的配置文件
models
├── __init__.py
├── tf.py
├── yolo.py
├── yolov5l.yaml
├── yolov5m.yaml
├── yolov5n.yaml
├── yolov5s.yaml
└── yolov5x.yaml
我们以 yolov5s.yaml 为例展开讲解。
2.1 模型深度系数 depth_multiple 和宽度系数 width_multiple
# Parameters
nc: 80 # number of classes | 类别数
depth_multiple: 0.33 # model depth multiple | 模型深度: 控制 BottleneckCSP 数
width_multiple: 0.50 # layer channel multiple | 模型宽度: 控制 Conv 通道个数(卷积核数量)
depth_multiple表示 BottleneckCSP、C3 等层缩放因子,将所有的 BottleneckCSP、C3等 模块的 Bottleneck 子模块 乘上该参数得到最终的 Bottleneck 子模块个数width_multiple表示卷积通道的缩放因子,就是将配置里的backbone和head部分(其实就是所有的)有关Conv的通道都需要乘上该系数
通过 depth_multiple 和 width_multiple 参数可以实现不同复杂度的模型设计:yolov5x、yolov5s、yolov5n、yolov5m、yolov5l。
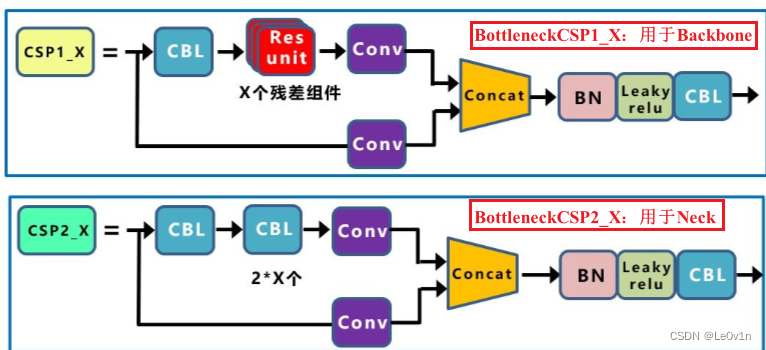
BotteleneckCSP 图片来源: 深入浅出Yolo系列之Yolov5核心基础知识完整讲解


2.2 anchors | 先验框大小
anchors:
- [10, 13, 16, 30, 33, 23] # P3/8
- [30, 61, 62, 45, 59, 119] # P4/16
- [116, 90, 156, 198, 373, 326] # P5/32
上面就定义了三种尺寸的先验框的大小,其中:
P3/8:P3是层的名称,8表示此时特征图经过的下采样大小 → P3 特征图此时已经过了 8 倍下采样P4/16:P4 特征图此时已经过了 16 倍下采样P5/32:P5 特征图此时已经过了 32 倍下采样
在 YOLOv5 中,P3 代表 Feature Pyramid Network (FPN) 的第三个级别。FPN 是一种用于目标检测的特征提取网络结构,它通过在不同层级的特征图上应用卷积和上采样操作,以获取具有不同尺度和语义信息的特征图。这些特征图可以用于检测不同大小的目标。
在这个模型配置文件中,P3/8 表示 P3 层在输入图像上的缩放因子为 8。缩放因子指的是在输入图像上的每个像素点在 P3 层特征图上所对应的尺寸。通过这种缩放,可以使得 P3 层特征图的尺寸相对于输入图像缩小 8 倍。这种缩放操作帮助模型捕获不同尺度的目标信息。
2.3 backbone
# YOLOv5 v6.0 backbone
backbone:
# [from, number, module, args]
[
[-1, 1, Conv, [64, 6, 2, 2]], # 0-P1/2
[-1, 1, Conv, [128, 3, 2]], # 1-P2/4
[-1, 3, C3, [128]],
[-1, 1, Conv, [256, 3, 2]], # 3-P3/8
[-1, 6, C3, [256]],
[-1, 1, Conv, [512, 3, 2]], # 5-P4/16
[-1, 9, C3, [512]],
[-1, 1, Conv, [1024, 3, 2]], # 7-P5/32
[-1, 3, C3, [1024]],
[-1, 1, SPPF, [1024, 5]], # 9
]
首先第一行的备注信息已经告诉我们了,这个 backbone 是 YOLOv5 和 YOLOv6 的 backbone。第二行中有对每一列的说明,其中:
from:表示输入的来源。-1 表示前一层的输出作为输入。number:表示重复使用该模块的次数。module:表示使用的特征提取模块类型。args:表示模块的参数:- Conv 层:输出通道数、卷积核大小、步幅和填充
- C3 层:输出通道数
- SPPF 层:表示输出通道数和池化的
kernel_size。
💡 注意:
- 在之前的版本(v4.0)中,backbone 的第一层是一个 Focus 层,但现在是一个卷积层。
- 对于 C3 层而言,如果重复了 3 次,且
stride=2,那么只有第一个 C3 模块会进行两倍下采样,剩下的两个 C3 模块不会进行下采样操作
〔与模型深度系数 depth_multiple 和宽度系数 width_multiple 的联系〕
前面说过了 depth_multiple 和 width_multiple 这两个参数的作用,对于 YOLOv5-s 的 C3 层而言,此时的 depth_multiple=0.33,那么第二列的 C3 层个数并不是实际上的数量,实际上的数量还得乘上 depth_multiple:
# YOLOv5 v6.0 backbone
backbone:
# [from, number, module, args]
[
[-1, 1, Conv, [64, 6, 2, 2]], # 0-P1/2
[-1, 1, Conv, [128, 3, 2]], # 1-P2/4
[-1, 3, C3, [128]], # 3*0.33=0.99 ---------> 实际使用1个C3
[-1, 1, Conv, [256, 3, 2]], # 3-P3/8
[-1, 6, C3, [256]], # 6*0.33=1.98 ---------> 实际使用2个C3
[-1, 1, Conv, [512, 3, 2]], # 5-P4/16
[-1, 9, C3, [512]], # 9*0.33=2.97 ---------> 实际使用3个C3
[-1, 1, Conv, [1024, 3, 2]], # 7-P5/32
[-1, 3, C3, [1024]], # 3*0.33=0.99 ---------> 实际使用1个C3
[-1, 1, SPPF, [1024, 5]], # 9
]
Question:这个计算是怎么进行的?
Answer:在 models/yolo.py 的 parse_model() 函数中有写:
# 对 backbone 和 head 中的所有层进行遍历
for i, (f, n, m, args) in enumerate(d["backbone"] + d["head"]):
# f <-> from:表示输入的来源。-1 表示前一层的输出作为输入。
# n <-> number:表示重复使用该模块的次数。
# m <-> module:表示使用的特征提取模块类型。
# args:表示模块的参数:
# 将字符串转换为对应的代码名称(不懂的看一下 eval 函数)
m = eval(m) if isinstance(m, str) else m
# 遍历每一层的参数args
for j, a in enumerate(args):
# j: 参数的索引
# a: 具体的参数
with contextlib.suppress(NameError):
# 将数字或字符长转换为代码
args[j] = eval(a) if isinstance(a, str) else a # eval strings
# 先将所有的 number 乘上 深度系数
n = n_ = max(round(n * gd), 1) if n > 1 else n # depth gain
这个根据向上取整的操作,并确保结果至少为 1
那么对于 width_multiple 系数而言,也是一样的(在 YOLOv5s 中, width_multiple=0.50):
# YOLOv5 v6.0 backbone
backbone:
# [from, number, module, args]
[
[-1, 1, Conv, [64, 6, 2, 2]], # 0-P1/2 ----------> 64 * 0.5 = 32
[-1, 1, Conv, [128, 3, 2]], # 1-P2/4 ----------> 128 * 0.5 = 64
[-1, 3, C3, [128]], # ----------> 128 * 0.5 = 64
[-1, 1, Conv, [256, 3, 2]], # 3-P3/8 ----------> 256 * 0.5 = 128
[-1, 6, C3, [256]], # ----------> 256 * 0.5 = 128
[-1, 1, Conv, [512, 3, 2]], # 5-P4/16 ----------> 512 * 0.5 = 256
[-1, 9, C3, [512]], # ----------> 512 * 0.5 = 256
[-1, 1, Conv, [1024, 3, 2]], # 7-P5/32 ----------> 1024* 0.5 = 512
[-1, 3, C3, [1024]], # ----------> 1024* 0.5 = 512
[-1, 1, SPPF, [1024, 5]], # 9 ----------> 1024* 0.5 = 512
]
意思就是说,将所有的卷积层都乘上 width_multiple,那我们看一下代码细节(还是在 models/yolo.py -> parse_model() 中):
# 对 backbone 和 head 中的所有层进行遍历
for i, (f, n, m, args) in enumerate(d["backbone"] + d["head"]):
# f <-> from:表示输入的来源。-1 表示前一层的输出作为输入。
# n <-> number:表示重复使用该模块的次数。
# m <-> module:表示使用的特征提取模块类型。
# args:表示模块的参数:
# 将字符串转换为对应的代码名称(不懂的看一下 eval 函数)
m = eval(m) if isinstance(m, str) else m
# 遍历每一层的参数args
for j, a in enumerate(args):
# j: 参数的索引
# a: 具体的参数
with contextlib.suppress(NameError):
# 将数字或字符长转换为代码
args[j] = eval(a) if isinstance(a, str) else a # eval strings
# 先将所有的 number 乘上 深度系数
n = n_ = max(round(n * gd), 1) if n > 1 else n # depth gain
# 判断当前模块是否在这个字典中
if m in {
Conv, # Conv + BN + SiLU
GhostConv, # 华为在 GhostNet 中提出的Ghost卷积
Bottleneck, # ResNet同款
GhostBottleneck, # 将其中的3x3卷积替换为GhostConv
SPP, # Spatial Pyramid Pooling
SPPF, # SPP + Conv
DWConv, # 深度卷积
MixConv2d, # 一种多尺度卷积层,可以在不同尺度上进行卷积操作。它使用多个不同大小的卷积核对输入特征图进行卷积,并将结果进行融合
Focus, # 一种特征聚焦层,用于减少计算量并增加感受野。它通过将输入特征图进行通道重排和降采样操作,以获取更稠密和更大感受野的特征图
CrossConv, # 一种交叉卷积层,用于增加特征图的多样性。它使用不同大小的卷积核对输入特征图进行卷积,并将结果进行融合
BottleneckCSP, # 一种基于残差结构的卷积块,由连续的Bottleneck模块和CSP(Cross Stage Partial)结构组成,用于构建深层网络,提高特征提取能力
C3, # 一种卷积块,由三个连续的卷积层组成。它用于提取特征,并增加网络的非线性能力
C3TR, # C3TR是C3的变体,它在C3的基础上添加了Transpose卷积操作。Transpose卷积用于将特征图的尺寸进行上采样
C3SPP, # C3SPP是C3的变体,它在C3的基础上添加了SPP操作。这样可以在不同尺度上对特征图进行池化,并增加网络的感受野
C3Ghost, # C3Ghost是一种基于C3模块的变体,它使用GhostConv代替传统的卷积操作
nn.ConvTranspose2d, # 转置卷积
DWConvTranspose2d, # DWConvTranspose2d是深度可分离的转置卷积层,用于进行上采样操作。它使用逐点卷积进行特征图的通道之间的信息整合,以减少计算量
C3x, # C3x是一种改进的C3模块,它在C3的基础上添加了额外的操作,如注意力机制或其他模块。这样可以进一步提高网络的性能
}:
c1, c2 = ch[f], args[0] # c1: 卷积的输入通道数, c2: 卷积的输出通道数 | ch[f] 上一次的输出通道数(即本层的输入通道数),args[0]:配置文件中想要的输出通道数
if c2 != no: # if not output
c2 = make_divisible(c2 * gw, ch_mul) # 让输出通道数*width_multiple
args = [c1, c2, *args[1:]] # 此时的c2已经是修改后的c2乘上width_multiple的c2了 | *args[1:]将其他非输出通道数的参数解包
# 如果当前层是 BottleneckCSP, C3, C3TR, C3Ghost, C3x 中的一种(这些结构都有 Bottleneck 结构)
if m in {BottleneckCSP, C3, C3TR, C3Ghost, C3x}:
args.insert(2, n) # number of repeats | 需要让Bottleneck重复n次
n = 1 # 重置n(其他层没有 Bottleneck 的模块不需要重复)
# 如果是BN层
elif m is nn.BatchNorm2d:
args = [ch[f]] # 确定输出通道数
# 如果是 Concat 层
elif m is Concat:
c2 = sum(ch[x] for x in f) # Concat是按着通道维度进行的,所以通道会增加
2.4 head
# YOLOv5 v6.0 head
head: [
[-1, 1, Conv, [512, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, "nearest"]],
[[-1, 6], 1, Concat, [1]], # cat backbone P4
[-1, 3, C3, [512, False]], # 13
[-1, 1, Conv, [256, 1, 1]],
[-1, 1, nn.Upsample, [None, 2, "nearest"]],
[[-1, 4], 1, Concat, [1]], # cat backbone P3
[-1, 3, C3, [256, False]], # 17 (P3/8-small)
[-1, 1, Conv, [256, 3, 2]],
[[-1, 14], 1, Concat, [1]], # cat head P4
[-1, 3, C3, [512, False]], # 20 (P4/16-medium)
[-1, 1, Conv, [512, 3, 2]],
[[-1, 10], 1, Concat, [1]], # cat head P5
[-1, 3, C3, [1024, False]], # 23 (P5/32-large)
[[17, 20, 23], 1, Detect, [nc, anchors]], # Detect(P3, P4, P5)
]
💡 Tips:
- 列的定义和 backbone 是一样的
- 不像 YOLOv3 那样,作者区分了 Neck 和 Head。YOLOv5 的作者没有做出区分,只有 Head,所以在 Head 部分中包含了 PANet 和 Detect 部分。
Question:Concat 怎么理解?
Answer:我们看下面的图。
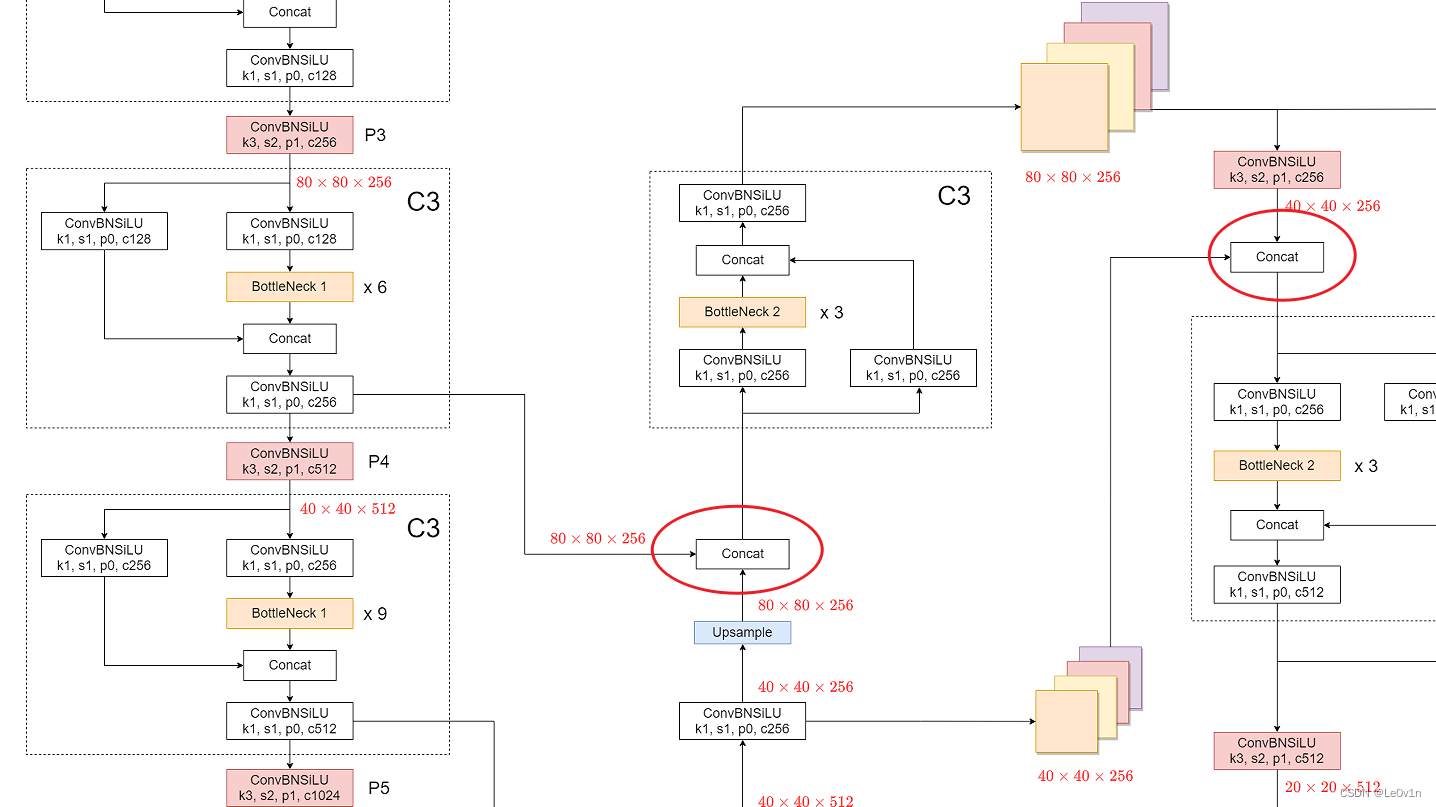
这里的 Concat 就是把浅层的特征图与当前特征图进行拼接(沿通道维度),我们看一下源码(在 models/common.py -> Concat 中):
class Concat(nn.Module):
# Concatenate a list of tensors along dimension
def __init__(self, dimension=1):
super().__init__()
self.d = dimension
def forward(self, x):
# 这里的 x 是一个 list,所以可以有多个 Tensor 进行拼接
return torch.cat(x, self.d)
这里需要注意的其实就是 from,即谁和谁拼接?下面是解释:
# YOLOv5 v6.0 backbone
backbone:
# [from, number, module, args]
[
[-1, 1, Conv, [64, 6, 2, 2]], # 0-P1/2
[-1, 1, Conv, [128, 3, 2]], # 1-P2/4
[-1, 3, C3, [128]], # 2
[-1, 1, Conv, [256, 3, 2]], # 3-P3/8
[-1, 6, C3, [256]], # 4
[-1, 1, Conv, [512, 3, 2]], # 5-P4/16
[-1, 9, C3, [512]], # 6
[-1, 1, Conv, [1024, 3, 2]], # 7-P5/32
[-1, 3, C3, [1024]], # 8
[-1, 1, SPPF, [1024, 5]], # 9
]
# YOLOv5 v6.0 head
head: [
[-1, 1, Conv, [512, 1, 1]], # 10
[-1, 1, nn.Upsample, [None, 2, "nearest"]], # 11
[[-1, 6], 1, Concat, [1]], # cat backbone P4 # 12
[-1, 3, C3, [512, False]], # 13
[-1, 1, Conv, [256, 1, 1]], # 14
[-1, 1, nn.Upsample, [None, 2, "nearest"]], # 15
[[-1, 4], 1, Concat, [1]], # cat backbone P3 # 16
[-1, 3, C3, [256, False]], # 17 (P3/8-small)
[-1, 1, Conv, [256, 3, 2]], # 18
[[-1, 14], 1, Concat, [1]], # cat head P4 # 19
[-1, 3, C3, [512, False]], # 20 (P4/16-medium)
[-1, 1, Conv, [512, 3, 2]], # 21
[[-1, 10], 1, Concat, [1]], # cat head P5 # 22
[-1, 3, C3, [1024, False]], # 23 (P5/32-large)
[[17, 20, 23], 1, Detect, [nc, anchors]], # Detect(P3, P4, P5) # 24
]
我们看第一个 Concat:[[-1, 6], 1, Concat, [1]]:
-1表示上一层(即 Concat 的前一层)6表示第 6 层,即 backbone 中的[-1, 9, C3, [512]]。
剩下的以此类推。
⚠️ 这里的索引是从 0 开始的
在 Head 中,P 其实对应的是检测头对应的输出层。比如说 P3 就是 8 倍下采样的输出层。我们常用的是 P3+P4+P5。为了捕获更小的目标,我们可以使用 models/hub/yolov5-p2.yaml 这个模型:

2.5 不同规格模型配置
| Model | size (pixels) | mAPval 50-95 | mAPval 50 | Speed CPU b1 (ms) | Speed V100 b1 (ms) | Speed V100 b32 (ms) | params (M) | FLOPs @640 (B) |
|---|---|---|---|---|---|---|---|---|
| YOLOv5n | 640 | 28.0 | 45.7 | 45 | 6.3 | 0.6 | 1.9 | 4.5 |
| YOLOv5s | 640 | 37.4 | 56.8 | 98 | 6.4 | 0.9 | 7.2 | 16.5 |
| YOLOv5m | 640 | 45.4 | 64.1 | 224 | 8.2 | 1.7 | 21.2 | 49.0 |
| YOLOv5l | 640 | 49.0 | 67.3 | 430 | 10.1 | 2.7 | 46.5 | 109.1 |
| YOLOv5x | 640 | 50.7 | 68.9 | 766 | 12.1 | 4.8 | 86.7 | 205.7 |
| YOLOv5n6 | 1280 | 36.0 | 54.4 | 153 | 8.1 | 2.1 | 3.2 | 4.6 |
| YOLOv5s6 | 1280 | 44.8 | 63.7 | 385 | 8.2 | 3.6 | 12.6 | 16.8 |
| YOLOv5m6 | 1280 | 51.3 | 69.3 | 887 | 11.1 | 6.8 | 35.7 | 50.0 |
| YOLOv5l6 | 1280 | 53.7 | 71.3 | 1784 | 15.8 | 10.5 | 76.8 | 111.4 |
| YOLOv5x6 + [TTA] | 1280 1536 | 55.0 55.8 | 72.7 72.7 | 3136 - | 26.2 - | 19.4 - | 140.7 - | 209.8 - |
Question:YOLOv5s 和 YOLOv5s6 有什么区别?
Answer:在YOLOv5中,"x6"表示YOLOv5的最大版本,并且具有更深和更宽的网络结构。可见 issue -> What is the difference between YOLOv5s and YOLOv5s6? #12499
Question:[TTA] 是什么?
Answer:TTA(Test Time Augmentation)是一种在测试时应用数据增强的技术。在目标检测任务中,通常会在训练时应用数据增强(如随机裁剪、旋转、缩放等)来增加训练样本的多样性,从而提高模型的鲁棒性和泛化能力。而在测试时,为了进一步提高模型的性能,可以应用一些额外的数据增强操作。TTA通过对输入图像进行多种增强操作,生成多个预测结果,并对这些结果进行综合,以提高目标检测模型的性能。可见官方介绍文档 -> 测试时间增强(TTA)
3. 网络架构
3.1 〔已废弃〕Focus
Focus 模块是 YOLOv5 中的一种卷积块,主要用于减少计算量和参数数量,并且能够保持较好的感受野。它通过将输入张量进行切分和重排来实现这一目标。目前最新的 YOLOv5 已不再使用该模块,而是使用一个 kernel=6, stride=2, padding=2 的 CBS 模块进行了替代。Focus 模块示意图如下所示。
CBS:
Conv -> BN -> SiLU
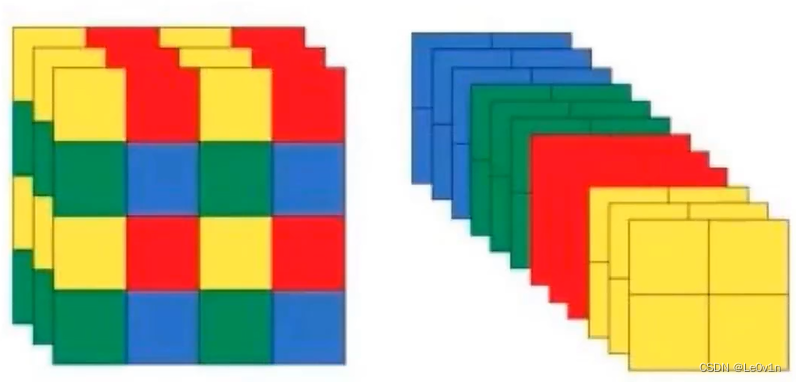
左边是原始输入,Focus 模块会把数据切分为 4 份,每份数据相当于是经过 2 倍下采样得到的,然后再在 Channel 维度进行拼接,最后再进行卷积操作。
我们看一下 Focus 模块的源码:
class Focus(nn.Module):
# Focus wh information into c-space | 将宽高信息聚焦到通道维度中
def __init__(self, c1, c2, k=1, s=1, p=None, g=1, act=True): # ch_in, ch_out, kernel, stride, padding, groups
super().__init__()
self.conv = Conv(c1 * 4, c2, k, s, p, g, act=act)
# self.contract = Contract(gain=2)
def forward(self, x): # x(b,c,w,h) -> y(b,4c,w/2,h/2)
return self.conv(torch.cat((x[..., ::2, ::2], x[..., 1::2, ::2], x[..., ::2, 1::2], x[..., 1::2, 1::2]), 1))
# return self.conv(self.contract(x))
其中的 Conv 模块如下:
class Conv(nn.Module):
# Standard convolution with args(ch_in, ch_out, kernel, stride, padding, groups, dilation, activation)
default_act = nn.SiLU() # default activation
def __init__(self, c1, c2, k=1, s=1, p=None, g=1, d=1, act=True):
super().__init__()
self.conv = nn.Conv2d(c1, c2, k, s, autopad(k, p, d), groups=g, dilation=d, bias=False)
self.bn = nn.BatchNorm2d(c2)
self.act = self.default_act if act is True else act if isinstance(act, nn.Module) else nn.Identity()
def forward(self, x):
return self.act(self.bn(self.conv(x)))
def forward_fuse(self, x): # 正常调用不会使用这个函数
return self.act(self.conv(x))
⚠️ Note: Conv 模块使用的激活函数是 SiLU 而非 ReLU。
那我们使用 Focus 模块试一试。
import torch
import torch.nn as nn
import os
import sys
import platform
from pathlib import Path
FILE = Path(__file__).resolve()
ROOT = FILE.parents[1] # YOLOv5 root directory
if str(ROOT) not in sys.path:
sys.path.append(str(ROOT)) # add ROOT to PATH
if platform.system() != "Windows":
ROOT = Path(os.path.relpath(ROOT, Path.cwd())) # relative
from common import Conv
class Focus(nn.Module):
# Focus wh information into c-space
def __init__(self, c1, c2, k=1, s=1, p=None, g=1, act=True): # ch_in, ch_out, kernel, stride, padding, groups
super().__init__()
self.conv = Conv(c1 * 4, c2, k, s, p, g, act=act)
# self.contract = Contract(gain=2)
def forward(self, x): # x(b,c,w,h) -> y(b,4c,w/2,h/2)
_concat = torch.cat((x[..., ::2, ::2], x[..., 1::2, ::2], x[..., ::2, 1::2], x[..., 1::2, 1::2]), 1)
_conv = self.conv(_concat)
print(f"{_concat = }")
print(f"{_concat.shape = }")
print(f"{_concat.dtype = }\n")
# print(f"{_conv = }")
print(f"{_conv.shape = }")
print(f"{_conv.dtype = }\n")
return _conv
# return self.conv(self.contract(x))
if __name__ == "__main__":
# 创建tensor
input_tensor = torch.tensor(data=[[[
[11, 12, 13, 14],
[21, 22, 23, 24],
[31, 32, 33, 34],
[41, 42, 43, 44]]]], dtype=torch.float32)
print(f"{input_tensor = }")
print(f"{input_tensor.shape = }")
print(f"{input_tensor.dtype = }\n")
# 创建Focus子模块模型对象
Sub_module = Focus(1, 64).eval()
# 前向推理
output = Sub_module(input_tensor)
我们看一下输出:
input_tensor = tensor([[[[11., 12., 13., 14.],
[21., 22., 23., 24.],
[31., 32., 33., 34.],
[41., 42., 43., 44.]]]])
input_tensor.shape = torch.Size([1, 1, 4, 4])
input_tensor.dtype = torch.float32
_concat = tensor([[[[11., 13.],
[31., 33.]],
[[21., 23.],
[41., 43.]],
[[12., 14.],
[32., 34.]],
[[22., 24.],
[42., 44.]]]])
_concat.shape = torch.Size([1, 4, 2, 2])
_concat.dtype = torch.float32
_conv.shape = torch.Size([1, 64, 2, 2])
_conv.dtype = torch.float32
〔分析〕假设我们的输入如下:
input_tensor = tensor([[[[11., 12., 13., 14.],
[21., 22., 23., 24.],
[31., 32., 33., 34.],
[41., 42., 43., 44.]]]])
input_tensor.shape = torch.Size([1, 1, 4, 4])
input_tensor.dtype = torch.float32
那么经过 torch.cat((x[..., ::2, ::2], x[..., 1::2, ::2], x[..., ::2, 1::2], x[..., 1::2, 1::2]), 1) 之后变为:
_concat = tensor([[[[11., 13.],
[31., 33.]],
[[21., 23.],
[41., 43.]],
[[12., 14.],
[32., 34.]],
[[22., 24.],
[42., 44.]]]])
_concat.shape = torch.Size([1, 4, 2, 2])
_concat.dtype = torch.float32
之后再经过一个卷积(self.conv(_concat))得到:
_conv.shape = torch.Size([1, 64, 2, 2])
_conv.dtype = torch.float32
可以看到,我们的输入从原来的 [1, 1, 4, 4] 变为了 [1, 4, 2, 2],之后再通过一个 CBS 卷积得到 Focus 的最终输入 [1, 64, 2, 2]。
那假设我们的输入是 [1, 3, 256, 256],那么是怎么变化的呢,结果如下:
input_tensor.shape = torch.Size([1, 3, 256, 256])
_concat.shape = torch.Size([1, 12, 128, 128])
_conv.shape = torch.Size([1, 64, 128, 128])
💡 总结:
- Focus 会对输入图片进行切片操作:
[N, C, H, W] -> [N, C*4, H//2, W//2] - 之后通过一个卷积,变成我们想要的 channel:
[N, C*4, H//2, W//2] -> [N, C_out, H//2, W//2]
可能有同学比较好奇,这个 Focus 模块出自哪篇论文,其实并没有论文,这是 YOLOv5 作者自己提出来的,下面是他的解释 @YOLOv5 Focus() Layer #3181
我收到了很多关于 YOLOv5 🚀 Focus 层的兴趣,因此我在这里写了一个简短的文档。在将 YOLOv3 架构演进为 YOLOv5 时,我自己创建了 Focus 层,并没有采用其他来源的方法。Focus 层的主要目的是减少层的数量、减少参数、减少 FLOPS、减少 CUDA 内存,同时最小程度地影响 mAP,提高前向和后向推理速度。
YOLOv5 的 Focus 层用单一层替换了 YOLOv3 的前 3 层:
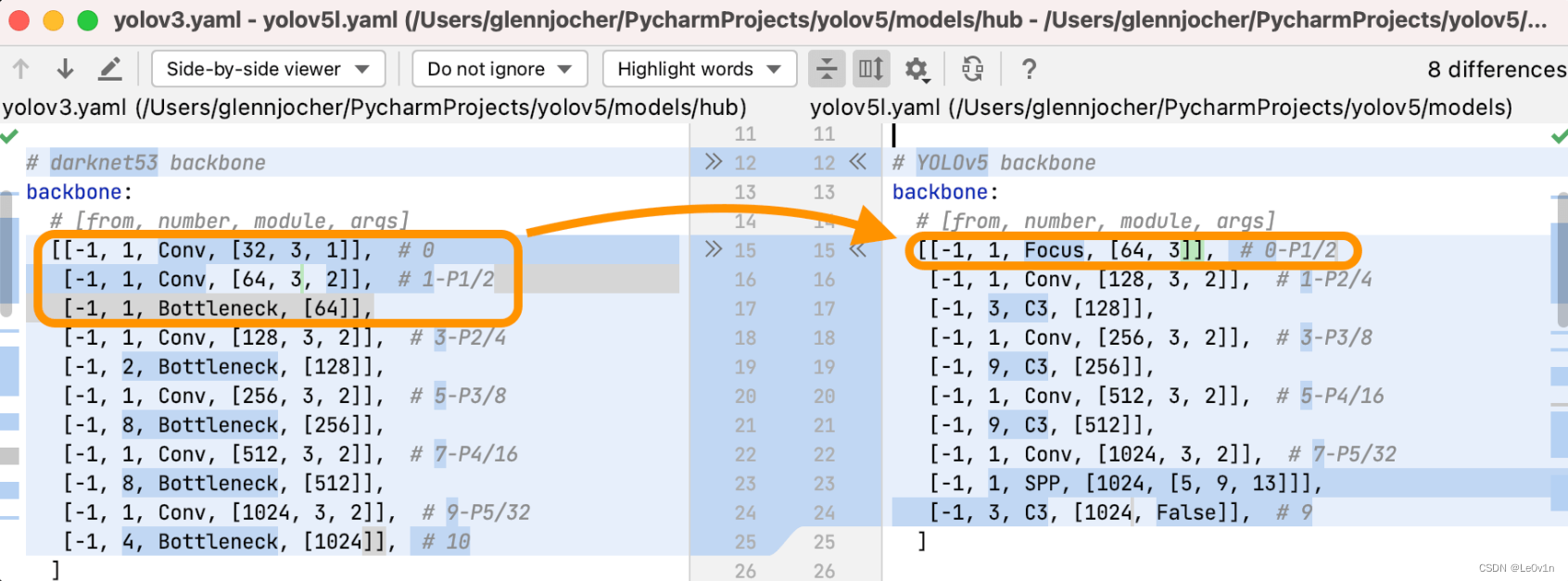
在大量尝试和分析了替代 YOLOv3 输入层的不同设计后,我最终选择了当前的 Focus 层设计。这些尝试包括对前向/后向/内存进行实时分析以及对完整的 300 个 Epoch 的 COCO 训练进行比较,以确定其对 mAP 的影响。您可以使用 YOLOv5 的
profile()函数很容易地对比 Focus 层和替代的 YOLOv3 原始层进行分析:# Profile import torch.nn as nn from models.common import Focus, Conv, Bottleneck from utils.torch_utils import profile m1 = Focus(3, 64, 3) # YOLOv5 Focus layer m2 = nn.Sequential(Conv(3, 32, 3, 1), Conv(32, 64, 3, 2), Bottleneck(64, 64)) # YOLOv3 first 3 layers results = profile(input=torch.randn(16, 3, 640, 640), ops=[m1, m2], n=10, device=0) # profile both 10 times at batch-size 16在 YOLOv5 Google Colab 笔记本中,我得到了以下结果:
YOLOv5 🚀 v5.0-405-gfad57c2 torch 1.9.0+cu102 CUDA:0 (Tesla T4, 15109.75MB) Params GFLOPs GPU_mem (GB) forward (ms) backward (ms) input output 7040 23.07 2.259 16.65 54.1 (16, 3, 640, 640) (16, 64, 320, 320) # Focus 40160 140.7 7.522 77.86 331.9 (16, 3, 640, 640) (16, 64, 320, 320) Params GFLOPs GPU_mem (GB) forward (ms) backward (ms) input output 7040 23.07 0.000 882.1 2029 (16, 3, 640, 640) (16, 64, 320, 320) # Focus 40160 140.7 0.000 4513 8565 (16, 3, 640, 640) (16, 64, 320, 320)
3.2 CSPNet(Cross Stage Partial Network)
CSPNet(Cross Stage Partial Network,跨阶段局部网络)旨在提高模型的性能,其的核心思想是在网络中引入 Cross Stage 信息传递,以促进不同阶段之间的信息流动,从而提高网络的感知能力。

在 ResNet 中,特征图会经过一系列的 Bottleneck 模块;而在 CSPNet 中,特征图会走两条支路,Part 1 中会直接短路,而 Part 2 中会经过 Bottleneck 模块,之后在 Partial Transition 中进行融合。
根据论文 CSPNet: A New Backbone that can Enhance Learning Capability of CNN,输入应该分为两个部分,分别通过两个独立的分支进行处理。但是在你的实现中,两个分支都使用相同的输入,且没有进行任何分割。
YOLOv5 的作者也对其进行了回答:
@abhiagwl4262 是的,输入并没有分割,它们在这里用于两个地方,我认为这与实际的 CSPNet 实现是一致的。
我们看一下 BottleneckCSP 的源码:
class BottleneckCSP(nn.Module):
# CSP Bottleneck https://github.com/WongKinYiu/CrossStagePartialNetworks
def __init__(self, c1, c2, n=1, shortcut=True, g=1, e=0.5): # ch_in, ch_out, number, shortcut, groups, expansion
super().__init__()
c_ = int(c2 * e) # hidden channels
self.cv1 = Conv(c1, c_, 1, 1) # CBS
self.cv2 = nn.Conv2d(c1, c_, 1, 1, bias=False) # 普通卷积
self.cv3 = nn.Conv2d(c_, c_, 1, 1, bias=False) # 普通卷积
self.cv4 = Conv(2 * c_, c2, 1, 1) # CBS
self.bn = nn.BatchNorm2d(2 * c_) # applied to cat(cv2, cv3)
self.act = nn.SiLU()
self.m = nn.Sequential(*(Bottleneck(c_, c_, shortcut, g, e=1.0) for _ in range(n)))
def forward(self, x):
_conv1 = self.cv1(x) # 经过 1x1 卷积(CBS)提升维度
_m = self.m(_conv1) # 经过一系列 Bottleneck 模块
y1 = self.cv3(_m) # 〔右边经过Bottleneck的分支〕再经过一个 1x1 普通卷积,没有升维也没有降维: c_
y2 = self.cv2(x) # 〔左边不经过Bottleneck的分支〕对原始的输入用 1x1 普通卷积降为: c_
_concat = torch.cat((y1, y2), 1) # 沿channel维度进行拼接: 2*c_
_bn = self.bn(_concat) # 经过BN层
_act = self.act(_bn) # 经过SiLU层
_conv4 = self.cv4(_act) # 使用 1x1 卷积(CBS)对融合后的特征图进行降维: c2 <=> c_out
return _conv4
可以看到,y1 就是一个特征图经过普通的 Bottleneck 得到的;y2 则只经过一个 1x1 卷积进行了通道维度对齐。
其实看了 BottleneckCSP 代码后我有一个疑问:
y1 = self.cv3(_m) # 〔右边经过Bottleneck的分支〕再经过一个 1x1 卷积,没有升维也没有降维: c_
这行代码有什么意义呢?因为 1x1 卷积本身的参数量就非常少,更何况 in_channel == out_channel,且 kernel_size=1,stride=1,这好像并没有做什么。让我们看一下 GPT 的回答:
self.cv3是一个具有c_输入通道和c_输出通道的 1x1 卷积层。这个操作应用于特征_m,并且不改变通道数。这一层的目的是引入非线性,并允许网络从经过转换的特征中学习复杂的模式。结果
y1是网络右侧分支的输出,经历了 bottleneck 模块的转换和额外的 1x1 卷积(self.cv3)。这个分支以一种捕捉复杂模式和经过 bottleneck 模块学到的相互作用的方式处理特征。总之,
y1 = self.cv3(_m)的目的在于引入非线性,并捕捉经过右侧分支 bottleneck 模块转换的特征中的复杂模式。两个分支的组合有助于提供丰富的信息,以便进行后续处理。
这个回答看似有一定的道理,但我感觉可能意义不大 😂。
3.3 C3(CSP Bottleneck with 3 convolutions)
现在的 YOLOv5 默认使用的 Bottleneck 模块并不是 BottleneckCSP 模块而是 C3 模块了,下面是 C3 模块的源码:
class C3(nn.Module):
# CSP Bottleneck with 3 convolutions
def __init__(self, c1, c2, n=1, shortcut=True, g=1, e=0.5): # ch_in, ch_out, number, shortcut, groups, expansion
super().__init__()
c_ = int(c2 * e) # hidden channels
self.cv1 = Conv(c1, c_, 1, 1) # CBS
self.cv2 = Conv(c1, c_, 1, 1) # CBS
self.cv3 = Conv(2 * c_, c2, 1) # CBS, optional act=FReLU(c2)
self.m = nn.Sequential(*(Bottleneck(c_, c_, shortcut, g, e=1.0) for _ in range(n)))
def forward(self, x):
_conv1 = self.cv1(x) # 输入fmap进行1x1卷积(CBS)降维: c1 -> c_
_m = self.m(_conv1) # 降维的fmap经过bottleneck: c_
_conv2 = self.cv2(x) # 输入fmap进行1x1卷积(CBS)降维: c1 -> c_
_concat = torch.cat((_m, _conv2), 1) # 沿channel维度进行拼接: 2*c_
_conv3 = self.cv3(_concat) # 将融合的fmap经过1x1卷积(CBS)升维: 2*c_ -> c2
return _conv3
可以看到:
- C3 模块中所有的卷积均为 CBS(Conv -> BN -> SiLU),不像 BottleneckCSP 中除了 CBS 外还会使用普通卷积。
- 还需要注意的是,在 BottleneckCSP 中,1x1 卷积用的是普通卷积,而在 C3 模块中,1x1 卷积用的是 CBS。
- 去掉了令我感到疑惑的 1x1 卷积 😂
除了上述 3 点外,剩下的与 BottleneckCSP 是一致的。可以这么说,C3 就是 BottleneckCSP 的高效版。
我们再看一篇论文:Model Compression Methods for YOLOv5: A Review,里面有这样一张图:
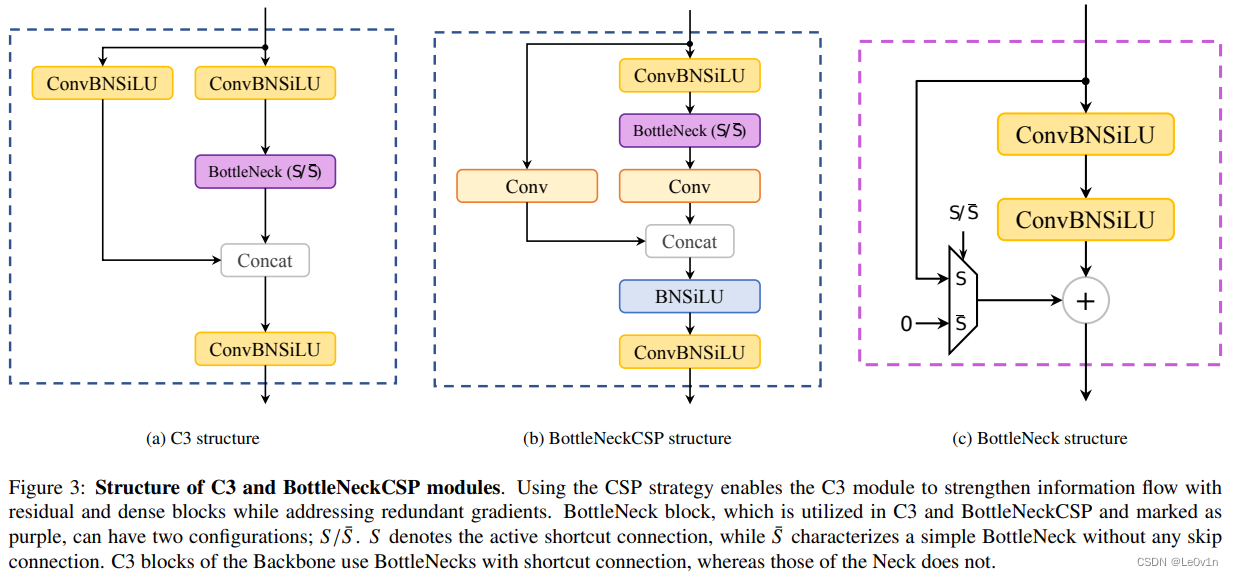
图 3:C3 和 BottleNeckCSP 模块的结构。使用 CSP 策略使 C3 模块通过残差块和稠密块加强信息流,同时解决冗余梯度的问题。BottleNeck 块在 C3 和 BottleNeckCSP 中被使用,并被标记为紫色,它可以有两种配置; S / S ‾ S/\overline{S} S/S。这里, S S S 表示激活的快捷连接,而 S ‾ \overline{S} S 表示没有任何跳跃连接的简单 BottleNeck。Backbone 中的 C3 块使用带有快捷连接的 BottleNecks,而 Neck 中的 C3 块则不使用。
从上面的图片我们可以看到,我们的说法遗漏了一个点:
- 在 BottleneckCSP 中,
concat之后会先经过一个BN -> SiLU的结构,最后再降维,而在 C3 中,没有这个BN -> SiLU结构。
我们再看一篇论文 MC-YOLOv5: A Multi-Class Small Object Detection Algorithm:

(a) C3 的结构,其输入为 H × W × C。C3 模块包含三个基本卷积层(CBS)和 n 个 Bottleneck 模块(n 由配置文件和网络深度确定),基本卷积的激活函数从 LeakyReLU 变为 SiLU。
(b) bottleneck-CSP 的结构,其输入为 H × W × C。它由普通卷积、CBL 和 ResUnit 结构组成。
和我们的说法没有冲突,那么我们可以再次总结我们的结论 —— C3 与 BottleneckCSP 的区别:
- C3 模块中所有的卷积均为 CBS(包括 1x1 卷积)
- 删除了 Bottleneck 后的 1x1 卷积
- C3 删除了
concat结构后的BN -> SiLU
Question:C3 模块为什么叫做 C3?
Answer:因为它的全称是:CSP Bottleneck with 3 convolutions。
3.4 SPP(Spatial Pyramid Pooling)
在 YOLOv5 中,SPP(Spatial Pyramid Pooling)是一种用于提取多尺度特征的技术,它有助于网络对不同尺度的目标进行检测。SPP 通过在不同大小的网格上进行池化操作,从而在不引入额外参数的情况下,捕捉输入特征图的不同尺度上的语义信息。
将 SPP 块添加到 CSP 之上,因为它显著增加了感受野,分离出最重要的上下文特征,并且几乎不会降低网络操作速度 —— YOLOv4 论文
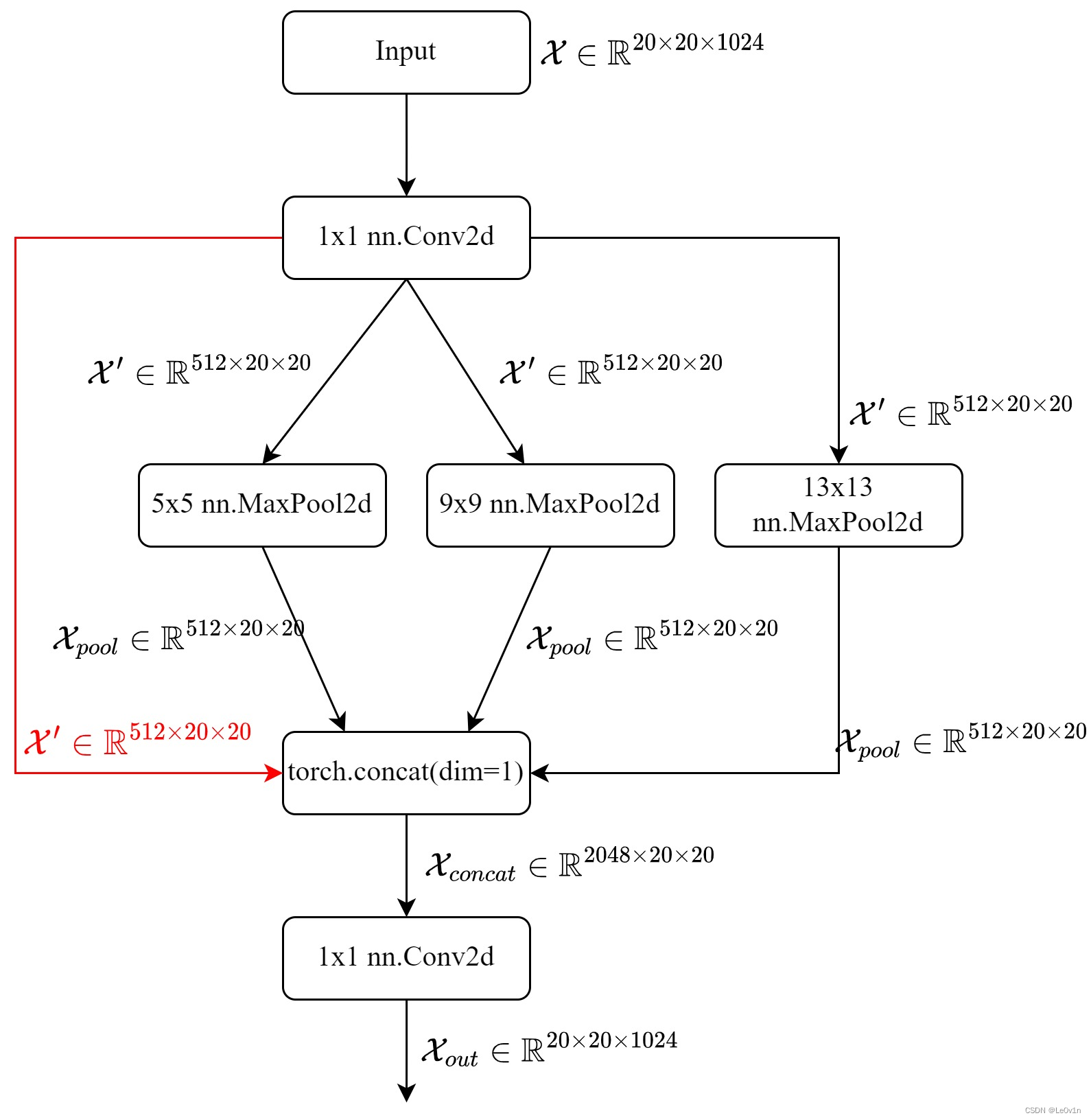
在 YOLOv4-SPP 中,进行了 5x5, 7x7, 13x13 的 MaxPooling,而在 YOLOv5-SPP 中,进行了 5x5, 9x9, 13x13 的 MaxPooling。通过 YOLOv4-SPP 中特征图变化可以看到,在进行了 MaxPooling 后特征图的 shape 并没有发生变化。我们看一下 YOLOv5-SPP 的源码:
class SPP(nn.Module):
# Spatial Pyramid Pooling (SPP) layer https://arxiv.org/abs/1406.4729
def __init__(self, c1, c2, k=(5, 9, 13)):
super().__init__()
c_ = c1 // 2 # hidden channels
self.cv1 = Conv(c1, c_, 1, 1)
self.cv2 = Conv(c_ * (len(k) + 1), c2, 1, 1) # 根据MaxPooling的个数自动调整,假设有3个MaxPooling则3+1=4
self.m = nn.ModuleList([nn.MaxPool2d(kernel_size=x, stride=1, padding=x // 2) for x in k])
def forward(self, x):
x = self.cv1(x) # 先经过一个 1x1 卷积调整通道数
_maxpools = [m(x) for m in self.m] # 经过一些列MaxPooling
_concat = torch.cat([x] + _maxpools, 1) # 将x与MaxPooling沿着通道维度拼接
_conv2 = self.cv2(_concat) # 最后经过一个1x1卷积调整通道数
return _conv2
不难理解,需要注意的是:
- 有 n 个 MaxPooling 层,Concat 后维度就会 x(n+1);
- SPP 中的池化层不会对特征图进行下采样
SPP 的流程图如下:
3.5 SPPF(Spatial Pyramid Pooling with Fixed)
SPP(Spatial Pyramid Pooling)和 SPPF(Spatial Pyramid Pooling with Fixed)都是在卷积神经网络(CNN)中使用的池化操作,旨在处理不同尺寸的输入图像,并生成固定大小的输出。
-
SPP(Spatial Pyramid Pooling):SPP 是由 Kaiming He 等人于 2014 年提出的,主要用于解决卷积神经网络在处理不同尺寸的输入图像时所面临的问题。在传统的 CNN 中,全连接层的输入大小是固定的,但是输入图像的大小可能会有所不同。SPP 的目标是通过不同大小的池化窗口,使网络能够接受不同尺寸的输入,并生成固定长度的特征向量。
-
SPPF(Spatial Pyramid Pooling with Fixed):SPPF 是在 SPP 的基础上进行改进的。SPPF 通过引入一个固定的金字塔级别(pyramid level),使得对输入图像的池化操作具有固定的感受野大小。这有助于在训练和推理中保持一致的输入特征大小。
总的来说,SPP 是一种池化策略,允许 CNN 处理不同尺寸的输入,而 SPPF 是对 SPP 的一种改进,引入了固定的金字塔级别,以提高输入和输出的一致性。这两者都在图像识别和目标检测等任务中取得了一定的成功。
我们看一下 SPPF 的源码:
class SPPF(nn.Module):
# Spatial Pyramid Pooling - Fast (SPPF) layer for YOLOv5 by Glenn Jocher
def __init__(self, c1, c2, k=5): # equivalent to SPP(k=(5, 9, 13))
super().__init__()
c_ = c1 // 2 # hidden channels
self.cv1 = Conv(c1, c_, 1, 1)
self.cv2 = Conv(c_ * 4, c2, 1, 1) # 这里不再是按照MaxPooling的个数进行的,而是固定为4
self.m = nn.MaxPool2d(kernel_size=k, stride=1, padding=k // 2) # 这里的模块不再是一系列,而是一个,且kernel_size被固定了!
def forward(self, x):
x = self.cv1(x) # 先经过一个 1x1 卷积
y1 = self.m(x) # 经过一个 5x5 的MaxPooling
y2 = self.m(y1) # 再经过一个 5x5 的MaxPooling
_m = self.m(y2) # 再再经过一个 5x5 的MaxPooling
_concat = torch.cat((x, y1, y2, _m), 1) # 将3个经过 MaxPooling 的和没有经过的沿着通道维度拼接
_conv2 = self.cv2(_concat) # 最后经过一个 1x1 卷积调整通道数
return _conv2
可以看到,SPPF 跟 SPP 有很大的区别,下面是 SPPF 的流程图:

放在一起看一下:

可以看到,SPPF 与 SPP 有了很大的不同:
- 在 SPP 中,经过 1x1 卷积的特征图 X \mathcal{X} X 会分为四条支路,分别进入 shortcut、5x5-MaxPooling、9x9-MaxPooling 以及 13x13-MaxPooling,之后四条支路的特征图会进行 Concat
- 在 SPPF 中,MaxPooling 的数量被固定为 4,且
kernel_size也被固定为k,经过 1x1 卷积的特征图 X \mathcal{X} X 会进入两条支路,左边还是 shortcut,右边则是顺序经过三个 5x5-MaxPooling,每个 MaxPooling 都会分为两个分支,一个进入 Concat,另外一个进入下一个 5x5-MaxPooling。
SPPF 这样的操作可以得到和 SPP 一样的模型性能,且计算量下降。
import sys
sys.path.append('Learning-Notebook-Codes/ObjectDetection/YOLOv5/codes/yolov5-v7.0')
from torchsummary import summary
from models.common import SPP, SPPF
spp = SPP(c1=32, c2=3)
sppf = SPPF(c1=32, c2=3)
summary(spp, (32, 26, 26))
summary(sppf, (32, 26, 26))
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 16, 26, 26] 512
BatchNorm2d-2 [-1, 16, 26, 26] 32
SiLU-3 [-1, 16, 26, 26] 0
SiLU-4 [-1, 16, 26, 26] 0
Conv-5 [-1, 16, 26, 26] 0
MaxPool2d-6 [-1, 16, 26, 26] 0
MaxPool2d-7 [-1, 16, 26, 26] 0
MaxPool2d-8 [-1, 16, 26, 26] 0
Conv2d-9 [-1, 3, 26, 26] 192
BatchNorm2d-10 [-1, 3, 26, 26] 6
SiLU-11 [-1, 3, 26, 26] 0
SiLU-12 [-1, 3, 26, 26] 0
Conv-13 [-1, 3, 26, 26] 0
================================================================
Total params: 742
Trainable params: 742
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.08
Forward/backward pass size (MB): 0.74
Params size (MB): 0.00
Estimated Total Size (MB): 0.82
----------------------------------------------------------------
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 16, 26, 26] 512
BatchNorm2d-2 [-1, 16, 26, 26] 32
SiLU-3 [-1, 16, 26, 26] 0
SiLU-4 [-1, 16, 26, 26] 0
Conv-5 [-1, 16, 26, 26] 0
MaxPool2d-6 [-1, 16, 26, 26] 0
MaxPool2d-7 [-1, 16, 26, 26] 0
MaxPool2d-8 [-1, 16, 26, 26] 0
Conv2d-9 [-1, 3, 26, 26] 192
BatchNorm2d-10 [-1, 3, 26, 26] 6
SiLU-11 [-1, 3, 26, 26] 0
SiLU-12 [-1, 3, 26, 26] 0
Conv-13 [-1, 3, 26, 26] 0
================================================================
Total params: 742
Trainable params: 742
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.08
Forward/backward pass size (MB): 0.74
Params size (MB): 0.00
Estimated Total Size (MB): 0.82
----------------------------------------------------------------
我们发现二者是一样的,因此直接暴力求解:
import sys
sys.path.append('Learning-Notebook-Codes/ObjectDetection/YOLOv5/codes/yolov5-v7.0')
import torch
import time
from tqdm.rich import tqdm
from models.common import SPP, SPPF
spp = SPP(c1=1024, c2=1024)
sppf = SPPF(c1=1024, c2=1024)
input_tensor = torch.randn(size=[1, 1024, 20, 20])
times = 200
t1 = time.time()
progress_bar = tqdm(total=times, desc='SPP')
for _ in range(times):
tmp = spp(input_tensor)
progress_bar.update()
progress_bar.close()
t2 = time.time()
progress_bar = tqdm(total=times, desc='SPPF')
for _ in range(times):
tmp = sppf(input_tensor)
progress_bar.update()
progress_bar.close()
t3 = time.time()
print(f"SPP (average time): {(t2 - t1) / times:.4f}s")
print(f"SPPF (average time): {(t3 - t2) / times:.4f}s")
SPP (average time): 0.0429s
SPPF (average time): 0.0250s
💡 可以看到,SPPF 的速度是 SPP 的 1.716 倍,提升是非常明显的!
3.6 PANet(Path-Aggregation Network)
PANet(Path-Aggregation Network,路径聚合网络)是一种用于目标检测的深度神经网络架构,旨在改善目标实例的多尺度特征表达。PANet 主要由两个关键组件组成:自顶向下的路径传播(Top-Down Path Propagation)和自底向上的特征聚合(Bottom-Up Feature Aggregation)。

(a) FPN主干网络。 (b) 自底向上路径增强。 © 自适应特征池化。 (d) 区域提取分支。 (e) 全连接融合。 注意,在(a)和(b)中为了简洁起见,我们省略了特征图的通道维度。
- 自顶向下的路径传播(Top-Down Path Propagation):
- PANet 通过自顶向下的路径传播从高层语义特征到低层细节特征,帮助网络更好地理解目标的全局和局部上下文信息。
- 这个传播路径使得网络能够通过多个层次的特征层次结合,从而捕捉目标的多尺度信息。
- 自底向上的特征聚合(Bottom-Up Feature Aggregation):
- 为了更好地捕获底层特征的细节信息,PANet 引入了自底向上的特征聚合机制。
- 通过底层特征的横向传播,网络能够聚合来自多个尺度的信息,有助于提升对小目标或者细节的检测性能。
PANet 的设计使得网络能够充分利用多尺度信息,从而提高目标检测任务的性能。该网络在 2018 年由北京大学的研究团队提出,已经在许多目标检测竞赛和应用中取得了显著的成果。这种网络架构的灵活性和高效性使得它在处理不同尺度和复杂场景下的目标检测问题上表现出色。
在 YOLOv5 架构图中,PANet 的示意图如下。
通过将拥有低中高层语义信息的特征图进行相互融合,最终的预测特征图不仅拥有高级语义信息,也有一定的中级和低级语义信息,这样可以提高模型预测能力。
4. 损失函数
YOLOv5 损失函数包括三种:
- Classification Loss:分类损失
- Localization Loss: 定位损失(Anchor 与 GT 框之间的误差)
- Confidence Loss: 置信度损失
总的损失是这三种损失的加权和。
4.1 分类损失
大多数分类器假设输出标签是互斥的(对于猫狗分类数据集而言,假设一张图片是“猫”,那么就不能是“狗”),例如 YOLOv1 和 YOLOv2,在这些模型中,通过使用 Softmax 函数将得分转换为总和为 1 的概率,以表示每个类别的置信度。然而,在 YOLOv3、YOLOv4 和 YOLOv5 之后,引入了多标签分类的概念。举个例子,YOLOv5 的输出标签可以是多标签的,例如一个检测框可能同时包含“行人”和“儿童”,这两个类别并不是互斥的。
Softmax 函数用于将一组实数转换为概率分布。给定输入向量 $ z = [z_1, z_2, …, z_k] $,Softmax 函数的输出 $ \sigma(z) $ 的计算公式如下:
σ ( z ) i = e z i ∑ j = 1 k e z j \sigma(z)_i = \frac{e^{z_i}}{\sum_{j=1}^{k} e^{z_j}} σ(z)i=∑j=1kezjezi
其中:
- $ \sigma(z)_i $ 是 Softmax 函数的输出中的第 $ i $ 个元素。
- $ e $ 是自然对数的底。
- $ z_i $ 是输入向量 $ z $ 的第 $ i $ 个元素。
- $ \sum_{j=1}^{k} e^{z_j} $ 是对所有输入向量的指数项的和。
Softmax 函数的目标是将输入向量 $ z $ 转换为一个概率分布,使得输出的每个元素都在 0 到 1 之间,且所有元素的和为 1。这通常用于多类别分类问题,其中每个元素对应一个类别,并且 Softmax 输出表示每个类别的概率。
需要注意的是,在多标签分类中,一个物体可能同时属于多个类别,因此输出的标签不再通过 Softmax 函数进行处理。相反,通常会使用 Sigmoid 函数对每个类别的得分进行独立的二分类处理。这样,每个类别的输出都是一个介于 0 和 1 之间的概率值,表示物体属于该类别的置信度。因此,在多标签分类下,输出类别的概率之和可以大于 1。
为了更清晰地说明多标签分类的实现方式,假设有 N 个类别,每个类别使用一个 Sigmoid 激活函数来产生一个范围在 0 到 1 之间的输出。对于每个类别,如果输出值大于设定的阈值(通常为 0.5),则认为该物体属于该类别。这种独立的二分类方式允许一个检测框同时具有多个类别,与互斥的单标签分类不同。
💡 总的来说,多标签分类通过使用多个独立的 Sigmoid 函数来实现,每个函数对应一个类别,这样就可以有效地处理一个物体属于多个类别的情况。
因此在计算分类损失时,YOLOv3、YOLOv4、YOLOv5 对每个标签都使用 BCE 损失,这样也降低了计算复杂度。
4.2 定位损失
4.2.1 IoU
边界框回归是许多 2D/3D 计算机视觉任务中最基本的组件之一。以前的方法通常使用 L 1 L_1 L1 和 L 2 L_2 L2 损失来度量边界框的预测误差,但这些损失函数考虑的因素相对较少。一种改进的方法是使用 IoU(Intersection over Union)来度量边界框的定位损失。
IoU 考虑了预测边界框与真实边界框之间的重叠程度,通过计算它们的交集与并集之间的比值。使用 IoU 作为损失函数的度量标准可以更准确地衡量边界框的位置和尺寸的预测精度,尤其是在目标检测等任务中。这种方法对于提高模型的定位准确性和鲁棒性非常有效。
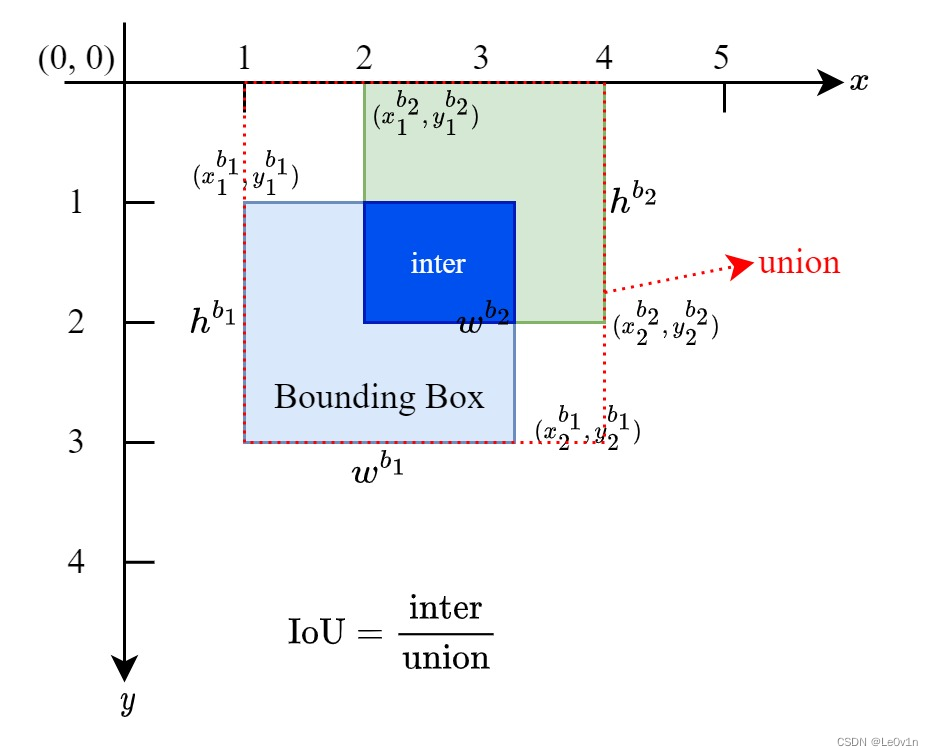
上图中,绿色的框为 Ground Truth,黑色的框为 Anchor,那么 IoU 计算公式如下:
I o U = ∣ A ∩ B ∣ ∣ A ∪ B ∣ \mathrm{IoU} = \frac{|A \cap B|}{|A \cup B|} IoU=∣A∪B∣∣A∩B∣
我们看一下 IoU 的源码:
def bbox_iou(box1, box2, xywh=True, GIoU=False, DIoU=False, CIoU=False, eps=1e-7):
"""
box1: [1, 4]
box2: [N, 4]
xywh: 坐标格式为 xywh
GIoU: 使用GIoU
DIoU: 使用DIoU
CIoU: 使用CIoU
"""
# Returns Intersection over Union (IoU) of box1(1,4) to box2(n,4)
# Get the coordinates of bounding boxes
# 将坐标转换为 xyxy 的格式
# ⚠️ 坐标原点:左上角
if xywh: # transform from xywh to xyxy
(x1, y1, w1, h1), (x2, y2, w2, h2) = box1.chunk(4, -1), box2.chunk(4, -1)
w1_, h1_, w2_, h2_ = w1 / 2, h1 / 2, w2 / 2, h2 / 2
b1_x1, b1_x2, b1_y1, b1_y2 = x1 - w1_, x1 + w1_, y1 - h1_, y1 + h1_
b2_x1, b2_x2, b2_y1, b2_y2 = x2 - w2_, x2 + w2_, y2 - h2_, y2 + h2_
else: # x1, y1, x2, y2 = box1
b1_x1, b1_y1, b1_x2, b1_y2 = box1.chunk(4, -1) # b1_x1: x1列
b2_x1, b2_y1, b2_x2, b2_y2 = box2.chunk(4, -1)
# 把w和h求出来
w1, h1 = b1_x2 - b1_x1, (b1_y2 - b1_y1).clamp(eps)
w2, h2 = b2_x2 - b2_x1, (b2_y2 - b2_y1).clamp(eps)
# Intersection area
# 求交集的面积
# tensor1.minimum(tensor2): 两个相同shape的tensor进行逐元素比较
inter_w = (b1_x2.minimum(b2_x2) - b1_x1.maximum(b2_x1)).clamp(0) # 交集的宽度
inter_h = (b1_y2.minimum(b2_y2) - b1_y1.maximum(b2_y1)).clamp(0) # 交集的高度
inter = inter_w * inter_h # 交集的面积
# Union Area
union = w1 * h1 + w2 * h2 - inter + eps
# IoU
iou = inter / union
return iou # IoU
对应的图片如下:
💡
torch.chunk(input, chunks, dim=0):input: 要分割的输入张量。chunks: 分割的块数。dim: 沿着哪个维度进行分割,默认为 0。💡
torch.clamp(input, min, max, out=None): 将输入张量的元素限制在指定范围内💡
torch.prod(input, dtype=None): 用于计算输入张量中所有元素的乘积💡
b1_x2.minimum(b2_x2)表示取b1_x2和b2_x2中的每个元素的最小值。这是一个逐元素的比较操作,对于两个形状相同的张量,它将返回一个新的张量,其中每个元素都是对应位置上两个输入张量中较小的那个值。
4.2.2 IoU 存在的问题
虽然 IoU 可以度量两个框的重合度,但也存在一定问题。当两个物体不重叠时,IoU 的计算结果为 0,这并不能直接反映出两个框的距离或定位误差。此外,当 IoU 被用作损失函数时,在两个框不重叠的情况下,梯度也为 0,这可能导致模型无法有效地进行优化,尤其是在训练初期。
if |A ∩ B| = 0:
IoU(A, B) = 0
4.2.3 IoU 推广:GIoU(Generalized IoU)
改进方法:为了解决 IoU 在不重叠的情况下的问题,一种常见的做法是推广 IoU 并确保满足以下条件:
- 遵循与 IoU 相同的定义:将比较对象的形状数据编码为区域属性。
- 维持 IoU 的尺寸不变性:确保新的指标在计算时不受对象尺寸变化的影响,保持与 IoU 相关的特性。
- 在重叠对象的情况下确保与 IoU 的强相关性:新的指标在两个对象高度重叠时应该保持与 IoU 类似的表现,以便保留其在目标检测等任务中的有效性。
在这个背景下,一种被提出的改进是 Generalized IoU(GIoU)。GIoU 是一种更全面的边界框重叠度量,它在计算两个边界框之间的重叠时,不仅考虑了它们的交集和并集,还考虑了它们的外接矩形(最小闭包矩形)。GIoU 被设计为在不同情况下都能提供更准确的重叠度量,包括不重叠的情况。GIoU 具体操作如下:
- 计算交集(Intersection): ∣ A ∩ B ∣ |A \cap B| ∣A∩B∣
- 计算并集(Union): ∣ A ∪ B ∣ |A \cup B| ∣A∪B∣
- 计算外接矩形的面积(Bounding Box的最小闭包矩形): ∣ C ∣ |C| ∣C∣
- 计算 GIoU: G I o U = I o U − ∣ C − ( A ∪ B ) ∣ ∣ C ∣ \mathrm{GIoU} = \mathrm{IoU} - \frac{|C - (A \cup B) |}{|C|} GIoU=IoU−∣C∣∣C−(A∪B)∣
- 计算损失值: L G I o U = 1 − G I o U \mathcal{L}_{\mathrm{GIoU}} = 1 - \mathrm{GIoU} LGIoU=1−GIoU

研究者们发现,使用 GIoU 作为损失函数在目标检测等任务中能够取得更好的性能,特别是在边界框回归方面。GIoU 的引入为解决 IoU 不足的问题提供了一个有效的方法。
我们看一下 GIoU 的源码:
def bbox_iou(box1, box2, xywh=True, GIoU=False, DIoU=False, CIoU=False, eps=1e-7):
# Returns Intersection over Union (IoU) of box1(1,4) to box2(n,4)
# Get the coordinates of bounding boxes
# 将坐标转换为 xyxy 的格式
# ⚠️ 坐标原点:左上角
if xywh: # transform from xywh to xyxy
(x1, y1, w1, h1), (x2, y2, w2, h2) = box1.chunk(4, -1), box2.chunk(4, -1)
w1_, h1_, w2_, h2_ = w1 / 2, h1 / 2, w2 / 2, h2 / 2
b1_x1, b1_x2, b1_y1, b1_y2 = x1 - w1_, x1 + w1_, y1 - h1_, y1 + h1_
b2_x1, b2_x2, b2_y1, b2_y2 = x2 - w2_, x2 + w2_, y2 - h2_, y2 + h2_
else: # x1, y1, x2, y2 = box1
b1_x1, b1_y1, b1_x2, b1_y2 = box1.chunk(4, -1) # b1_x1: x1列
b2_x1, b2_y1, b2_x2, b2_y2 = box2.chunk(4, -1)
# 把w和h求出来
w1, h1 = b1_x2 - b1_x1, (b1_y2 - b1_y1).clamp(eps)
w2, h2 = b2_x2 - b2_x1, (b2_y2 - b2_y1).clamp(eps)
# Intersection area
# 求交集的面积
# tensor1.minimum(tensor2): 两个相同shape的tensor进行逐元素比较
inter_w = (b1_x2.minimum(b2_x2) - b1_x1.maximum(b2_x1)).clamp(0) # 交集的宽度
inter_h = (b1_y2.minimum(b2_y2) - b1_y1.maximum(b2_y1)).clamp(0) # 交集的高度
inter = inter_w * inter_h # 交集的面积
# Union Area
union = w1 * h1 + w2 * h2 - inter + eps
# 先求一下普通的IoU
iou = inter / union
if CIoU or DIoU or GIoU:
# GIoU https://arxiv.org/pdf/1902.09630.pdf
# 求出最小外接矩形的宽度
cw = b1_x2.maximum(b2_x2) - b1_x1.minimum(b2_x1) # convex (smallest enclosing box) width
# 求出最小外接矩形的高度
ch = b1_y2.maximum(b2_y2) - b1_y1.minimum(b2_y1) # convex height
# 求出最小外接矩形的面积
c_area = cw * ch + eps # convex area
# 计算最终的 IoU
iou = iou - (c_area - union) / c_area
return iou
4.2.4 DIoU(Distance IoU)
Distance-IoU (DIoU) 是为了进一步改进边界框重叠度量而提出的。DIoU 是 GIoU 的一种改进形式,它在 GIoU 的基础上引入了对边界框中心点之间距离的考虑。DIoU 的提出主要是为了解决 GIoU 中的一些问题,尤其是在存在重叠但不完全匹配的情况下的不足。
GIoU 主要考虑了两个边界框的交集、并集以及外接矩形,但在一些情况下,GIoU 仍然可能受到边界框中心点之间距离的限制。在物体不完全对齐的情况下,GIoU 可能会导致对中心点距离的过度敏感,因此在一些实际场景中,GIoU 可能表现不够稳健。
DIoU 引入了中心点之间的距离,通过考虑中心点距离来纠正 GIoU 中的一些缺陷。DIoU 的计算包括了中心点距离的项,以更全面地度量两个边界框之间的距离。DIoU 在实际目标检测任务中的性能提升主要体现在对不完全匹配目标的准确边界框回归上。

Figure 5: DIoU loss for bounding box regression, where the normalized distance between central points can be directly minimized. c c c is the diagonal length of the smallest enclosing box covering two boxes, and d = ρ ( b , b g t ) d = \rho(\bold{b}, \bold{b}^{gt}) d=ρ(b,bgt) is the distance of central points of two boxes.
图5:DIoU损失用于边界框回归,其中可以直接最小化中心点之间的标准化距离。 c c c 是覆盖两个框的最小外接框的对角线长度, d = ρ ( b , b g t ) d = \rho(\bold{b}, \bold{b}^{gt}) d=ρ(b,bgt) 是两个框中心点的距离。
综合而言,DIoU 的提出旨在弥补 GIoU 中对中心点距离的过度敏感的问题,使得在处理实际场景中存在不完全匹配的目标时能够更加稳健。
我们看一下 DIoU 的源码:
def bbox_iou(box1, box2, xywh=True, GIoU=False, DIoU=False, CIoU=False, eps=1e-7):
# Returns Intersection over Union (IoU) of box1(1,4) to box2(n,4)
# Get the coordinates of bounding boxes
# 将坐标转换为 xyxy 的格式
# ⚠️ 坐标原点:左上角
if xywh: # transform from xywh to xyxy
(x1, y1, w1, h1), (x2, y2, w2, h2) = box1.chunk(4, -1), box2.chunk(4, -1)
w1_, h1_, w2_, h2_ = w1 / 2, h1 / 2, w2 / 2, h2 / 2
b1_x1, b1_x2, b1_y1, b1_y2 = x1 - w1_, x1 + w1_, y1 - h1_, y1 + h1_
b2_x1, b2_x2, b2_y1, b2_y2 = x2 - w2_, x2 + w2_, y2 - h2_, y2 + h2_
else: # x1, y1, x2, y2 = box1
b1_x1, b1_y1, b1_x2, b1_y2 = box1.chunk(4, -1) # b1_x1: x1列
b2_x1, b2_y1, b2_x2, b2_y2 = box2.chunk(4, -1)
# 把w和h求出来
w1, h1 = b1_x2 - b1_x1, (b1_y2 - b1_y1).clamp(eps)
w2, h2 = b2_x2 - b2_x1, (b2_y2 - b2_y1).clamp(eps)
# Intersection area
# 求交集的面积
# tensor1.minimum(tensor2): 两个相同shape的tensor进行逐元素比较
inter_w = (b1_x2.minimum(b2_x2) - b1_x1.maximum(b2_x1)).clamp(0) # 交集的宽度
inter_h = (b1_y2.minimum(b2_y2) - b1_y1.maximum(b2_y1)).clamp(0) # 交集的高度
inter = inter_w * inter_h # 交集的面积
# Union Area
union = w1 * h1 + w2 * h2 - inter + eps
# 先求一下普通的IoU
iou = inter / union
if CIoU or DIoU or GIoU:
# GIoU https://arxiv.org/pdf/1902.09630.pdf
# 求出最小外接矩形的宽度
cw = b1_x2.maximum(b2_x2) - b1_x1.minimum(b2_x1) # convex (smallest enclosing box) width
# 求出最小外接矩形的高度
ch = b1_y2.maximum(b2_y2) - b1_y1.minimum(b2_y1) # convex height
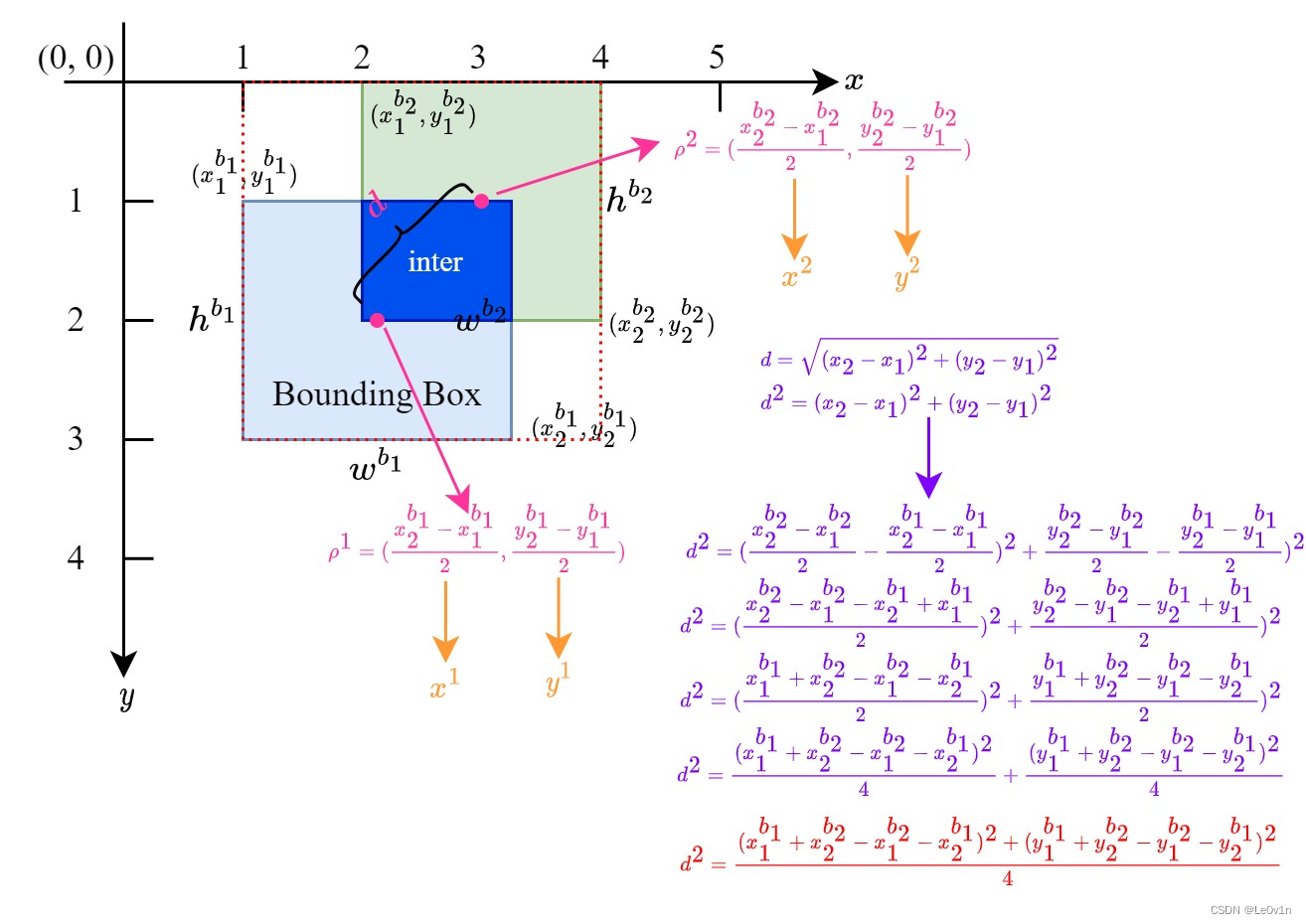
# Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
if CIoU or DIoU:
# 💡 使用勾股定理求出对角线的平方,即c^2
c² = cw**2 + ch**2 + eps # convex diagonal squared | 凸对角线的平方
# 求两个box中心点的平方(看下面的图)
rho² = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 + (b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4 # center dist ** 2
return iou - rho² / c² # DIoU
还是拿下面这张图说事儿,
4.2.5 CIoU(Complete IoU)
CIoU(Complete Intersection over Union)是一种边界框(Bounding Box)的相似性度量方法,它是 DIoU(Distance Intersection over Union)的改进版本。CIoU 主要用于目标检测任务中,特别是在训练阶段,作为损失函数的一部分。以下是DIoU的一些潜在缺陷:
-
局限性: DIoU 主要关注中心点距离和最小外接矩形对角线距离,相对于 CIoU 来说,DIoU 的度量相对较为简化,有时无法捕捉边界框之间的复杂关系。
-
对形状变化不敏感: DIoU 在处理边界框形状变化时可能不够敏感,特别是对于不同形状和比例的目标,DIoU 的相似性度量可能不够准确。
-
不全面: DIoU 缺乏对宽高比例差异的考虑,而 CIoU 引入了宽高比例差异的项,使得相似性度量更加全面。
-
收敛性较差: 在某些情况下,DIoU 可能在训练中收敛较慢,而 CIoU 的改进设计有助于提高损失函数的收敛性。
总的来说,CIoU 可以看作是对 DIoU 的一种扩展和改进,以更全面、更准确地度量边界框之间的相似性。在实践中,CIoU 的性能可能更好,特别是在处理各种目标形状和尺寸差异的情况下。然而,选择使用哪种方法通常取决于具体的任务和实验结果。
相比于 DIoU,CIoU 还考虑了宽高比例差异,即 CIoU 还考虑了两个边界框的宽高比例之差异。
CIoU 的计算公式如下:
CIoU = IoU − d 2 c 2 − α ⋅ v \text{CIoU} = \text{IoU} - \frac{d^2}{c^2} - \alpha \cdot v CIoU=IoU−c2d2−α⋅v
可以看到,相比于 DIoU,CIoU 其实只是在惩罚项上加了一项,即
R CIoU = ρ 2 ( b , b g t ) c 2 + α v \mathcal{R}_{\text{CIoU}} = \frac{\rho^2(\bold{b}, \bold{b}^{gt})}{c^2} + \alpha v RCIoU=c2ρ2(b,bgt)+αv
其中, α \alpha α 是一个正的权衡参数,而 v v v 衡量了两个 Box 宽高比的一致性:
v = 4 π 2 ( arctan w g t h g t − arctan w h ) 2 v = \frac{4}{\pi^2}(\arctan \frac{w^{gt}}{h^{gt}} - \arctan\frac{w}{h})^2 v=π24(arctanhgtwgt−arctanhw)2
CIoU 的损失函数定义如下:
L CIoU = 1 − I o U + ρ 2 ( b , b g t ) c 2 + α v \mathcal{L}_{\text{CIoU}} = 1 - \mathrm{IoU} + \frac{\rho^2(\bold{b}, \bold{b}^{gt})}{c^2} + \alpha v LCIoU=1−IoU+c2ρ2(b,bgt)+αv
其中权衡参数 α \alpha α 被定义为:
α = v ( 1 − I o U ) + v ′ \alpha = \frac{v}{(1 - IoU) + v'} α=(1−IoU)+v′v
通过这个定义,重叠区域因子在回归中被赋予更高的优先级,特别是对于非重叠情况。
最后,CIoU 损失的优化与 DIoU 损失相同,只是需要明确关于宽度(w)和高度(h)的 v v v 梯度:
∂ v ∂ w = 8 π 2 ( arctan w g t h g t − arctan w h ) × h w 2 + h 2 ∂ v ∂ h = 8 π 2 ( arctan w g t h g t − arctan w h ) × w w 2 + h 2 (12) \frac{\partial v}{\partial w} = \frac{8}{\pi^2}(\arctan \frac{w^{gt}}{h^{gt}} - \arctan \frac{w}{h}) \times \frac{h}{w^2 + h^2} \\ \frac{\partial v}{\partial h} = \frac{8}{\pi^2}(\arctan \frac{w^{gt}}{h^{gt}} - \arctan \frac{w}{h}) \times \frac{w}{w^2 + h^2} \tag{12} ∂w∂v=π28(arctanhgtwgt−arctanhw)×w2+h2h∂h∂v=π28(arctanhgtwgt−arctanhw)×w2+h2w(12)
分母 w 2 + h 2 w^2 + h^2 w2+h2 在 h h h 和 w w w 范围在 [0, 1] 的情况下通常是一个较小的值,可能导致梯度爆炸。因此,在我们的实现中,为了稳定收敛,分母 w 2 + h 2 w^2+h^2 w2+h2 被简单地移除,其中步长 1 w 2 + h 2 \frac{1}{w^2+h^2} w2+h21 被替换为1,梯度方向仍然与方程 (12) 一致。
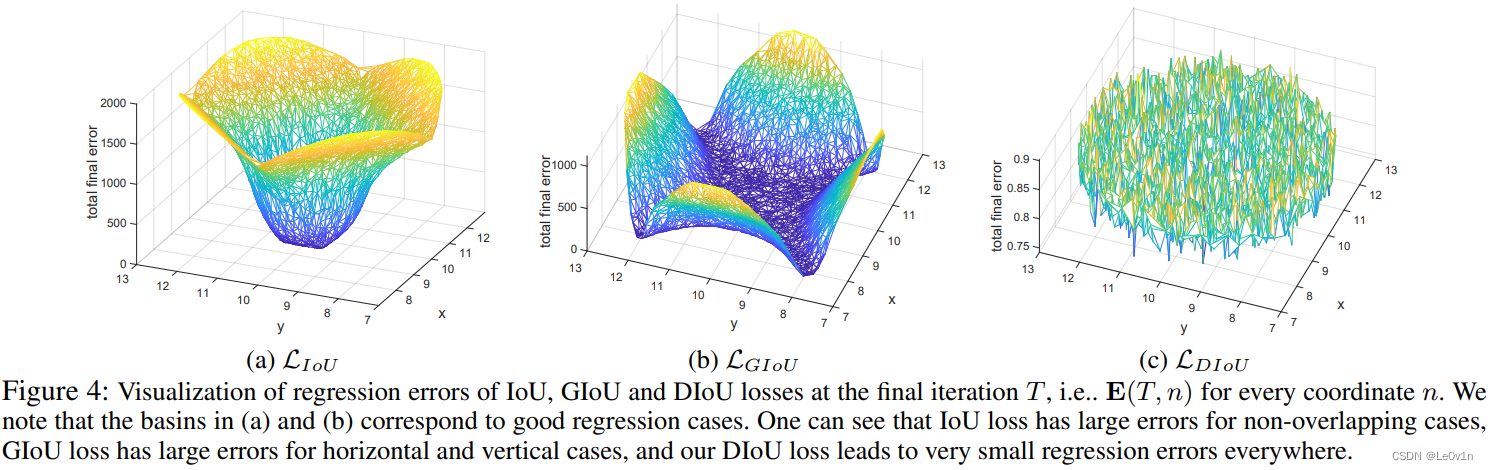
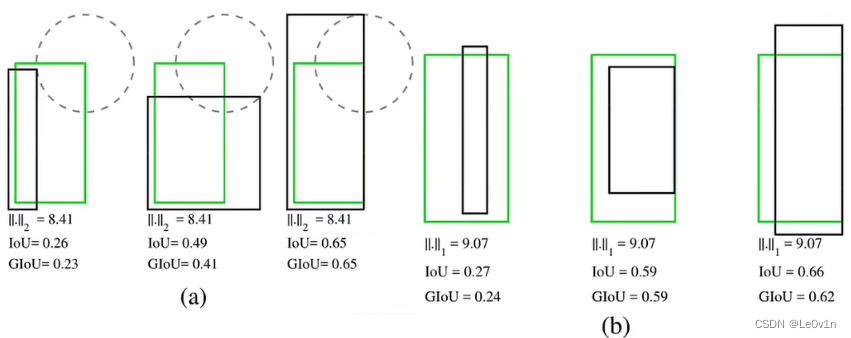
图4:在最终迭代 T T T(即 E ( T , n ) E(T, n) E(T,n))可视化了 IoU、GIoU 和 DIoU 损失的回归误差,对每个坐标 n n n。我们注意到 (a) 和 (b) 中的区域对应于良好的回归情况。可以看到,IoU 损失在非重叠情况下有较大误差,GIoU 损失在水平和垂直情况下有较大误差,而我们的 DIoU 损失在所有地方都导致非常小的回归误差。
我们看一下 CIoU 的源码:
def bbox_iou(box1, box2, xywh=True, GIoU=False, DIoU=False, CIoU=False, eps=1e-7):
# Returns Intersection over Union (IoU) of box1(1,4) to box2(n,4)
# Get the coordinates of bounding boxes
# 将坐标转换为 xyxy 的格式
# ⚠️ 坐标原点:左上角
if xywh: # transform from xywh to xyxy
(x1, y1, w1, h1), (x2, y2, w2, h2) = box1.chunk(4, -1), box2.chunk(4, -1)
w1_, h1_, w2_, h2_ = w1 / 2, h1 / 2, w2 / 2, h2 / 2
b1_x1, b1_x2, b1_y1, b1_y2 = x1 - w1_, x1 + w1_, y1 - h1_, y1 + h1_
b2_x1, b2_x2, b2_y1, b2_y2 = x2 - w2_, x2 + w2_, y2 - h2_, y2 + h2_
else: # x1, y1, x2, y2 = box1
b1_x1, b1_y1, b1_x2, b1_y2 = box1.chunk(4, -1) # b1_x1: x1列
b2_x1, b2_y1, b2_x2, b2_y2 = box2.chunk(4, -1)
# 把w和h求出来
w1, h1 = b1_x2 - b1_x1, (b1_y2 - b1_y1).clamp(eps)
w2, h2 = b2_x2 - b2_x1, (b2_y2 - b2_y1).clamp(eps)
# Intersection area
# 求交集的面积
# tensor1.minimum(tensor2): 两个相同shape的tensor进行逐元素比较
inter_w = (b1_x2.minimum(b2_x2) - b1_x1.maximum(b2_x1)).clamp(0) # 交集的宽度
inter_h = (b1_y2.minimum(b2_y2) - b1_y1.maximum(b2_y1)).clamp(0) # 交集的高度
inter = inter_w * inter_h # 交集的面积
# Union Area
union = w1 * h1 + w2 * h2 - inter + eps
# 先求一下普通的IoU
iou = inter / union
if CIoU or DIoU or GIoU:
# GIoU https://arxiv.org/pdf/1902.09630.pdf
# 求出最小外接矩形的宽度
cw = b1_x2.maximum(b2_x2) - b1_x1.minimum(b2_x1) # convex (smallest enclosing box) width
# 求出最小外接矩形的高度
ch = b1_y2.maximum(b2_y2) - b1_y1.minimum(b2_y1) # convex height
# Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
if CIoU or DIoU:
# 💡 使用勾股定理求出对角线的平方,即c^2
c² = cw**2 + ch**2 + eps # convex diagonal squared | 凸对角线的平方
# 求两个box中心点的平方(看下面的图)
rho² = ((b2_x1 + b2_x2 - b1_x1 - b1_x2) ** 2 + (b2_y1 + b2_y2 - b1_y1 - b1_y2) ** 2) / 4 # center dist ** 2
# 使用CIoU
if CIoU:
# 宽高比trade-off parameter
v = (4 / math.pi**2) * (torch.atan(w2 / h2) - torch.atan(w1 / h1)).pow(2)
# 当处于前向推理时
with torch.no_grad():
alpha = v / (v - iou + (1 + eps))
return iou - (rho2 / c2 + v * alpha) # CIoU
CIoU 的引入旨在提高边界框相似性度量的准确性,使得在目标检测的训练中更好地指导模型的学习。
4.3 YOLOv5 目标框回归与跨网格匹配策略
4.3.1 Box 的格式
首先我们回顾一下 PASCAL VOC 的标注格式。如下图所示,图片尺寸为 1000x654,把左上角作为坐标原点 (0,0)。

那么我们可以得到 xyxy 格式的坐标:
x1, y1 = 187, 21
x2, y2 = 403, 627
除了这种 xyxy 格式的坐标,还有一种常用的坐标格式为:xywh 格式的坐标,即:
x = x1 + (x2 - x1) / 2 # 295.0
y = y1 + (y2 - y1) / 2 # 324.0
上面的式子可以进行化简:
x = (x1 + x2) / 2 # 295.0
y = (y1 + y2) / 2 # 324.0
求出中心点坐标后,我们需要求出宽度和高度:
w = x2 - x1 # 216
h = y2 - y1 # 606
同理,如果我们知道 xywh 坐标如何求出 xyxy 坐标呢?
x, y, w, h = 295, 324, 216, 606
x1 = x - w / 2 # 187.0
y1 = y - h / 2 # 21.0
x2 = x + w / 2 # 403.0
y2 = y + h / 2 # 627.0
我们也可以将其写为函数:
def xyxy2xywh(xyxy):
"""
将边界框坐标格式从 (x_min, y_min, x_max, y_max) 转换为 (x_center, y_center, width, height)
"""
x_min, y_min, x_max, y_max = xyxy
x_center = (x_min + x_max) / 2
y_center = (y_min + y_max) / 2
width = x_max - x_min
height = y_max - y_min
return x_center, y_center, width, height
def xywh2xyxy(xywh):
"""
将边界框坐标格式从 (x_center, y_center, width, height) 转换为 (x_min, y_min, x_max, y_max)
"""
x_center, y_center, width, height = xywh
x_min = x_center - width / 2
y_min = y_center - height / 2
x_max = x_center + width / 2
y_max = y_center + height / 2
return x_min, y_min, x_max, y_max
我们看一下具体的标注格式内容:

<?xml version="1.0" encoding="utf-8"?>
<annotation>
<folder>images</folder>
<filename>000000000025.jpg</filename>
<size>
<width>640</width>
<height>426</height>
<depth>3</depth>
</size>
<object>
<name>giraffe</name>
<pose>Unspecified</pose>
<truncated>0</truncated>
<difficult>0</difficult>
<bndbox>
<xmin>385.52992</xmin>
<ymin>60.030002999999994</ymin>
<xmax>600.50016</xmax>
<ymax>357.19013700000005</ymax>
</bndbox>
</object>
<object>
<name>giraffe</name>
<pose>Unspecified</pose>
<truncated>0</truncated>
<difficult>0</difficult>
<bndbox>
<xmin>53.01024000000001</xmin>
<ymin>356.49000599999994</ymin>
<xmax>185.04032</xmax>
<ymax>411.68001</ymax>
</bndbox>
</object>
</annotation>
我们再看一下它对应的 .txt 标签:
23 0.770336 0.489695 0.335891 0.697559
23 0.185977 0.901608 0.206297 0.129554
可以看到,xml 中使用的标签格式是 xyxy,而 yolo 中使用的是 xywh。
其中 YOLO 格式的列分别表示:
class_id x y w h
23 0.770336 0.489695 0.335891 0.697559
23 0.185977 0.901608 0.206297 0.129554
⚠️ YOLO 格式中使用的是归一化后的坐标,即:
x: box 中心点横坐标 / 图片宽度y: box 中心点横坐标 / 图片高度w: box 宽度 / 图片宽度h: box 高度 / 图片高度

4.3.2 YOLOv3 和 YOLOv4 的目标框回归
先验框 Anchor 给出了目标宽高的初始值,需要回归的是目标真实宽高与初始宽高的偏移量。具体做法如下:
- 预测框中心点相对于对应网格左上角位置的相对偏移量
- 为了将边界框中心点约束在当前网格中,使用 sigmoid 函数处理偏移值,使预测偏移量的值在 (0,1) 范围内

图2:具有维度先验和位置预测的边界框。我们将边界框的宽度和高度预测为相对于聚类中心的偏移量。使用 sigmoid 函数,我们预测边界框的中心坐标相对于滤波器应用位置的位置。该图毫不掩饰地自引用自 [15]。
图中:
- 蓝色的框为预测框
- 黑色的框为 GT
根据边界框,模型会预测 4 个 offsets: t x , t y , t w , t h t_x, t_y, t_w, t_h tx,ty,tw,th,可以按照如下公式计算出边界框的实际位置和宽高:
b x = σ ( t x ) + c x b y = σ ( t y ) + c y b w = p w e t w b h = p h e t h \begin{aligned} b_x &= \sigma(t_x) + c_x \\ b_y &= \sigma(t_y) + c_y \\ b_w &= p_w e^{t_w}\\ b_h &= p_h e^{t_h} \end{aligned} bxbybwbh=σ(tx)+cx=σ(ty)+cy=pwetw=pheth
其中:
- t x t_x tx 和 t y t_y ty 是模型预测的相对于 Anchor 框(或先验框)的中心的偏移量。
- σ \sigma σ 表示 sigmoid 函数,它将预测的偏移量转换到 0 和 1 之间,这样就可以用来表示相对于特征图(feature map)上的特定点的位置。
- c x c_x cx 和 c y c_y cy 是 Anchor 框(或先验框)的中心坐标在特征图上的对应位置。
- b x b_x bx 和 b y b_y by 是预测框的中心坐标。
对于宽度和高度,公式稍有不同:
- p w p_w pw 和 p h p_h ph 是 Anchor 框(或先验框)的宽度和高度。
- t w t_w tw 和 t h t_h th 是模型预测的相对于 Anchor 框的宽度和高度的偏移量。
- e e e 是自然对数的底数,用于指数化预测的偏移量,这样可以保证宽度和高度始终为正数。
- b w b_w bw 和 b h b_h bh 是预测框的宽度和高度。
总的来说,这些公式描述了如何将模型的预测(偏移量和尺寸变化)应用于 Anchor 框,以得到最终的预测边界框。
Question: t x t_x tx 和 t y t_y ty 是相对于原图的偏移量吗?
Answer:不, t x t_x tx 和 t y t_y ty 不是相对于原图的偏移量。它们是相对于特定特征图(feature map)上的Anchor框(或先验框)中心的偏移量。
Question:为什么要给 t x t_x tx 和 t y t_y ty 添加 σ \sigma σ 函数?
Answer:在 YOLOv5 等物体检测模型中,给 t x t_x tx 和 t y t_y ty 添加 sigmoid 函数的原因是为了将预测的偏移量限制在 0 和 1 之间。这样做有以下几个原因:
- 归一化:sigmoid 函数将任何实数映射到 (0, 1) 区间内。在物体检测中,我们需要预测边界框的中心相对于特定网格单元(grid cell)的位置。通过使用 sigmoid 函数,我们可以确保预测的偏移量是归一化的,即它们表示的是相对于网格单元的比例,而不是绝对的坐标值。
- 稳定训练:在训练过程中,模型的输出可能会非常大或非常小,这可能导致数值不稳定,例如梯度消失或爆炸。sigmoid 函数的输出是平滑的,有助于减少这种不稳定性,使得训练过程更加稳定。
- 可解释性:归一化的偏移量更具有可解释性,因为它们直接表示边界框中心相对于网格单元的位置比例。例如,如果一个网格单元的尺寸是 16x16 像素,一个预测的 t x t_x tx 值为 0.5,那么边界框中心的 x 坐标将位于该网格单元的中心。
- 兼容性:在 YOLOv5 中,特征图上的每个点都对应于原始图像上的一个区域。通过使用 sigmoid 函数,模型可以更容易地适应不同尺寸的输入图像,因为偏移量是相对于网格单元的比例,而不是绝对的像素值。
总之,使用 sigmoid 函数是为了确保预测的边界框位置是归一化的、稳定的,并且可以跨不同尺寸的图像进行泛化。
Question:那么 t w t_w tw 和 t h t_h th 为什么要使用 e e e ?
Answer:在 YOLOv5 等物体检测模型中, t w t_w tw 和 t h t_h th(即预测的宽度和高度偏移量)使用指数函数(通常指的是自然指数函数 e x e^x ex)的原因是为了保证预测的宽度和高度是正数,并且可以取任意大的值。这样做有以下几个原因:
- 非负值保证:边界框的宽度和高度必须是正数。通过使用指数函数,我们可以确保即使预测的偏移量 t w t_w tw 和 t h t_h th 是负数,经过指数变换后的 b w b_w bw 和 b h b_h bh(即最终的宽度和高度)也是正数。
- 尺度变换的灵活性:自然指数函数 e x e^x ex 提供了一个连续且单调递增的变换,这意味着小的偏移量会导致小的尺度变化,而大的偏移量会导致大的尺度变化。这种变换的灵活性使得模型可以更好地适应不同大小和比例的物体。
- 数值稳定性:与 sigmoid 函数类似,指数函数也有助于提高数值稳定性。在训练过程中,模型可能会预测很大的负数作为宽度和高度的偏移量,直接使用这些值可能会导致数值问题。指数函数可以平滑这些极端值,从而提高训练的稳定性。
- 避免限制:如果使用其他函数(如线性函数或 ReLU)来变换宽度和高度的偏移量,可能会引入不必要的限制,例如宽度和高度的上限。指数函数没有这样的限制,因此可以更准确地预测各种大小的边界框。
4.3.3 YOLOv5 的目标框回归
YOLOv5 的目标框回归计算公式如下:

b x = 2 σ ( t x ) − 0.5 + c x b y = 2 σ ( t y ) − 0.5 + c y b w = p w ( 2 σ ( t w ) ) 2 b h = p h ( 2 σ ( t h ) ) 2 \begin{aligned} b_x &= 2\sigma(t_x) - 0.5 + c_x \\ b_y &= 2\sigma(t_y) - 0.5 + c_y \\ b_w &= p_w(2\sigma(t_w))^2 \\ b_h &= p_h(2\sigma(t_h))^2 \end{aligned} bxbybwbh=2σ(tx)−0.5+cx=2σ(ty)−0.5+cy=pw(2σ(tw))2=ph(2σ(th))2
与 YOLOv3 不同是的,YOLOv5 得到的所有预测值都需要经过 σ \sigma σ 函数,而且 b x , b y , b w , b h b_x, b_y, b_w, b_h bx,by,bw,bh 的求解都与 YOLOv3 有着区别。那么 YOLOv5 这么做也是有自己的考量:
原始的 YOLO/DarkNet 关于 Anchor 的公式存在严重的缺陷,宽度和高度完全不受限制,因为有一个指数的运算,这可能会导致训练时的梯度失控、不稳定、NaN 损失等等,并且最终无法完成训练。
对于 YOLOv5,确保通过 Sigmoid 函数对模型的所有输出进行运算从而纠正该问题。这样的损失函数也会增加正样本的个数(Anchor 的个数)。
4.3.4 YOLOv5 跨网格匹配策略
YOLOv5 采用了跨邻域网格的匹配策略,从而得到更多的正样本 Anchor,这可以加速模型收敛,具体做法为:
从当前网格的上、下、左、右的四个网格中找到离目标中心点最近的两个网络,再加上当前网格,这样一共会有三个网格进行匹配。

这样除了目标中心点落在区域内的网格①外,还会使用网格②和网格③。这样,正样本 Anchor 从原来的 1 扩充为 3。
参考资料
- YOLOv5入门到精通!不愧是公认的讲的最好的【目标检测全套教程】同济大佬12小时带你从入门到进阶(YOLO/目标检测/环境部署+项目实战/Python/)