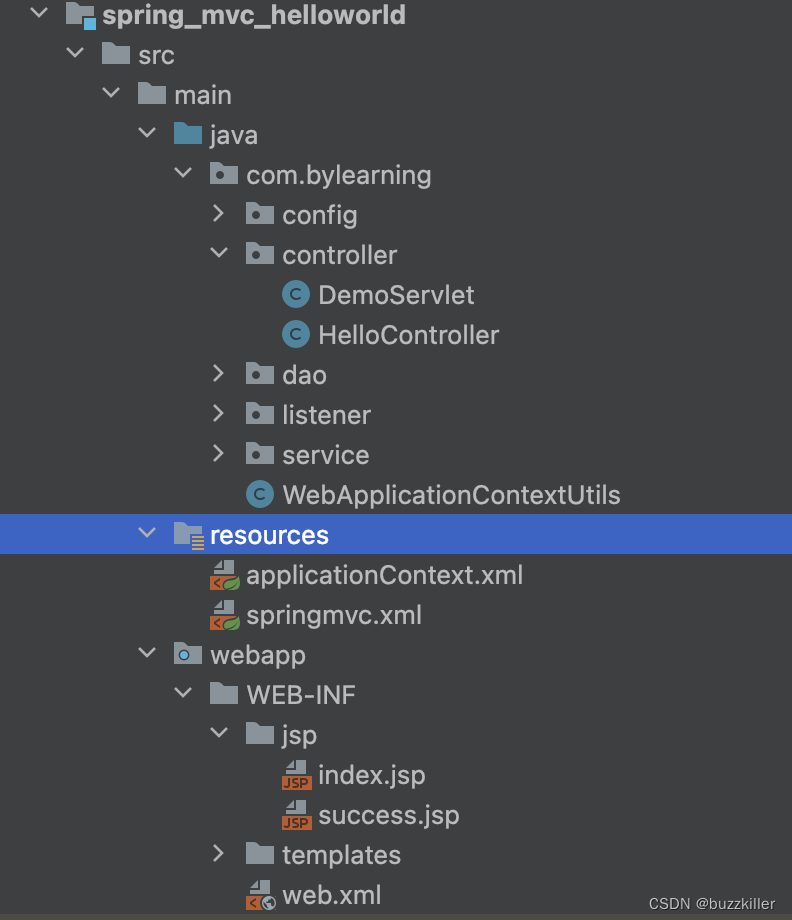
题目描述

小埋最近在玩一个解密游戏，这个游戏的解密方法是这样的，这个游戏会给你提供  个数,让我们求出这  个数里面，有多少个连续的数的平均数大于某个给定的数  。这个数可能会很大，所以我们要输出这个数对 的取模结果。现在小埋对于这个游戏的解法还是不太理解，现在请你帮助小埋解决这个问题。

输入格式

输入有两行。第一行为两个数 和  。第二行为 个数。

输出格式

输出的数占一行，即问题的解对  取模的结果。

样例 #1

样例输入 #1

4 3 
1 5 4 2

样例输出 #1

5

样例 #2

样例输入 #2

4 4 5 2 7 3

样例输出 #2

6

提示

所有的数均为正整数且不大于5000

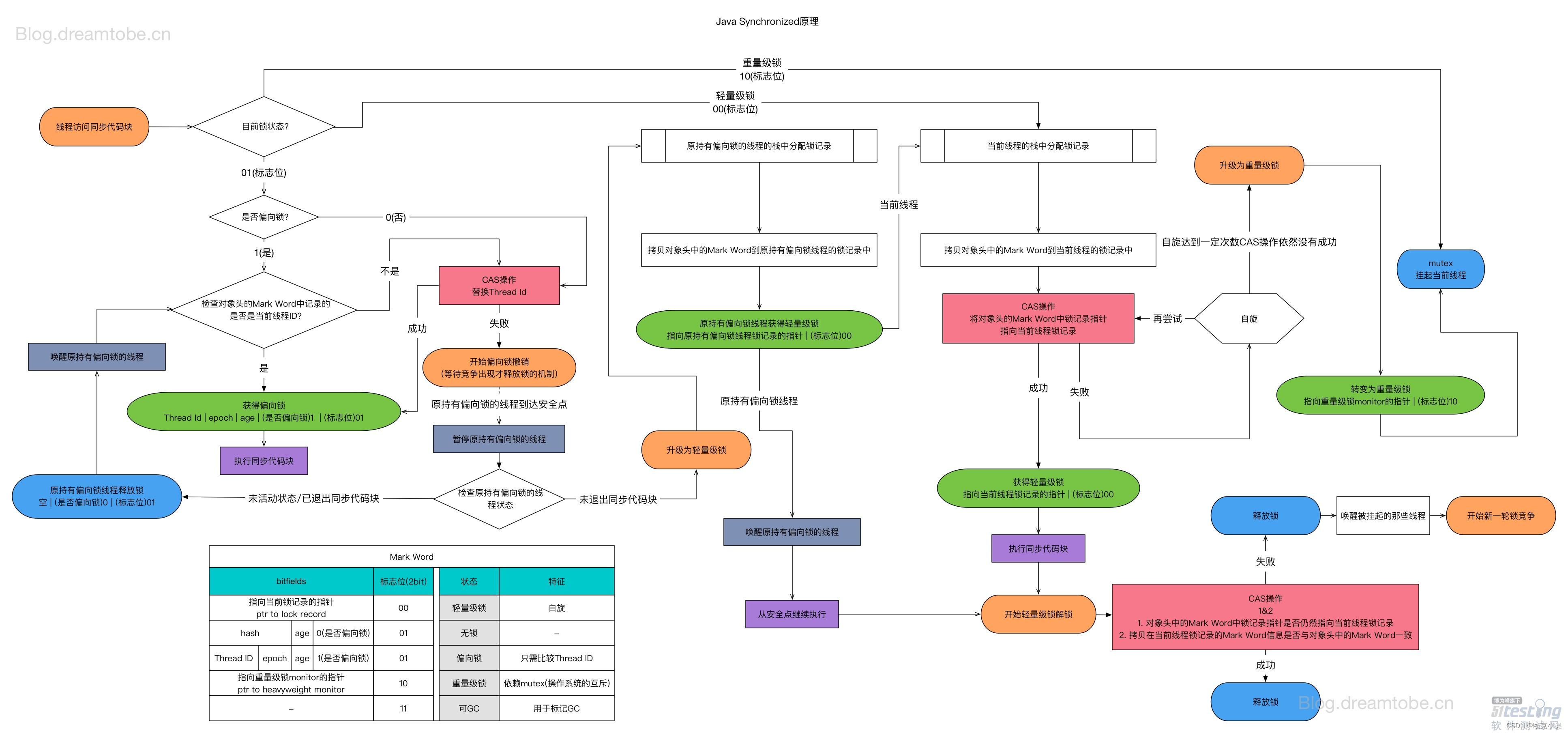
主要思路：

这个题目。由于是平均数>m，所以我们可以将所有的数-m，求一遍前缀和，进行归并排序，求出所有的正序对（i<j,且a[i]<a[j])的数对。

代码实现code：

#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
int a[200010],b[200010];
long long ret=0;
int shu[200010];
void merge(int l,int r)
{
	if(l == r)
	{
		return;
	}
	int mid=(l+r)/2;
	merge(l,mid);
	merge(mid+1,r);//归并排序分治
	int i=l,j=mid+1,tot=l;
	while(i<=mid&&j<=r)
	{
		if(a[i]<a[j])
		{
			ret+=(mid-i+1)%mod;
			ret%=mod;
			b[tot++]=a[j++];	
		}
		else
		{
			b[tot++]=a[i++];
		}
	}
	while(i<=mid)
	{
		b[tot++]=a[i++];	
	}
	while(j<=r)
	{
		b[tot++]=a[j++];
	}//区间合并
	for(int i=l;i<=r;i++)
	{
		a[i]=b[i];
	}
}
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>shu[i];
		shu[i]-=m;
		a[i] = a[i-1]+shu[i];
	}
	merge(0,n);
	cout<<ret;
	return 0;
}