2024/1/30 dfs与bfs

news2024/9/23 1:26:47

想要了解dfs与bfs，就得了解队列和栈。

一、栈与队列

1.栈

栈说白了就是先入后出。把栈类比为一个容器。只有一个口，所以如果我们想要取出最底层也就是最先放入的元素，只能最后取出它。

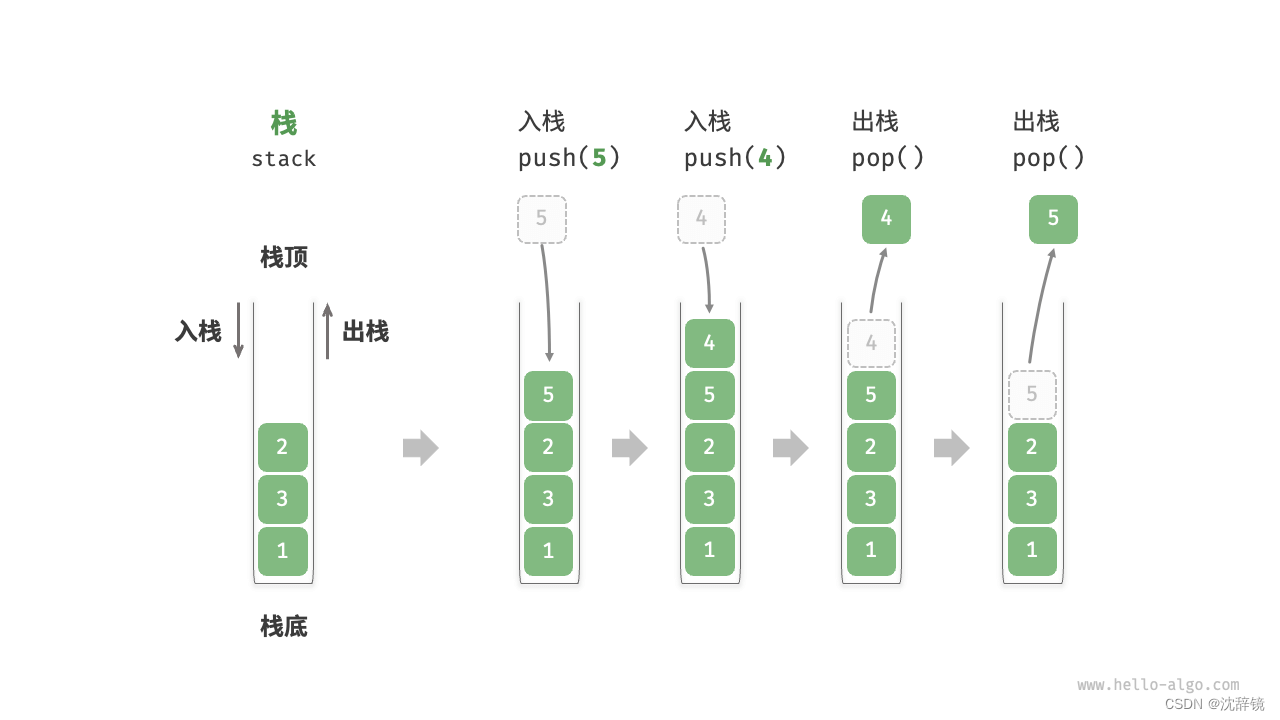
栈基础操作有如下几种：

  1. push 放入
  2. pop 拿出
  3. empty 是否为空
  4. size 栈的大小
  5. top 获取栈顶元素

下面将用两种方式实现：

  1. 用数组或者链表模拟栈 
    #include <iostream>
using namespace std;

const int N = 100;

int stk[N], top = 0;

int main()
{

	//使用数组模拟栈
	int x;
	cin >> x;
	//push放入栈中
	stk[++top] = x;
	//输出栈顶元素
	cout << stk[top] << endl;
	//pop拿出(不管top元素删不删，top--就行)
	top--;
	// 常用的就是，获取栈顶元素的同时，弹出栈顶元素
	int u = stk[top--];


	return 0;
}

    以上是普通静态数组。但是考虑到现实生活由于入栈的元素可能会源源不断地增加，因此我们可以使用动态数组或者链表，这样就无须自行处理数组扩容问题。这里贴出hello算法里对这个的网址。https://www.hello-algo.com/chapter_stack_and_queue/stack/#1icon-default.png?t=N7T8https://www.hello-algo.com/chapter_stack_and_queue/stack/#1

  2. stl库写栈

首先就是 #include <stack>

定义：stack<数据类型> stk;

使用：

  • stk.push(x);
  • stk.pop();
  • stk.top();
  • stk.empty();//true表示空
  • stk.size();//返回正整数
#include <iostream>
#include <stack>
using namespace std;


int main()
{
	stack<int>stk;
	int x;
	cin >> x;
	//放入栈中
	stk.push(x);
	//输出栈顶
	cout << stk.top() << endl;
	//弹出栈顶
	stk.pop();
	return 0;
}

2.队列

队列则是：“先入先出”。「队列 queue」是一种遵循先入先出规则的线性数据结构。顾名思义，队列模拟了排队现象，即新来的人不断加入队列尾部，而位于队列头部的人逐个离开。

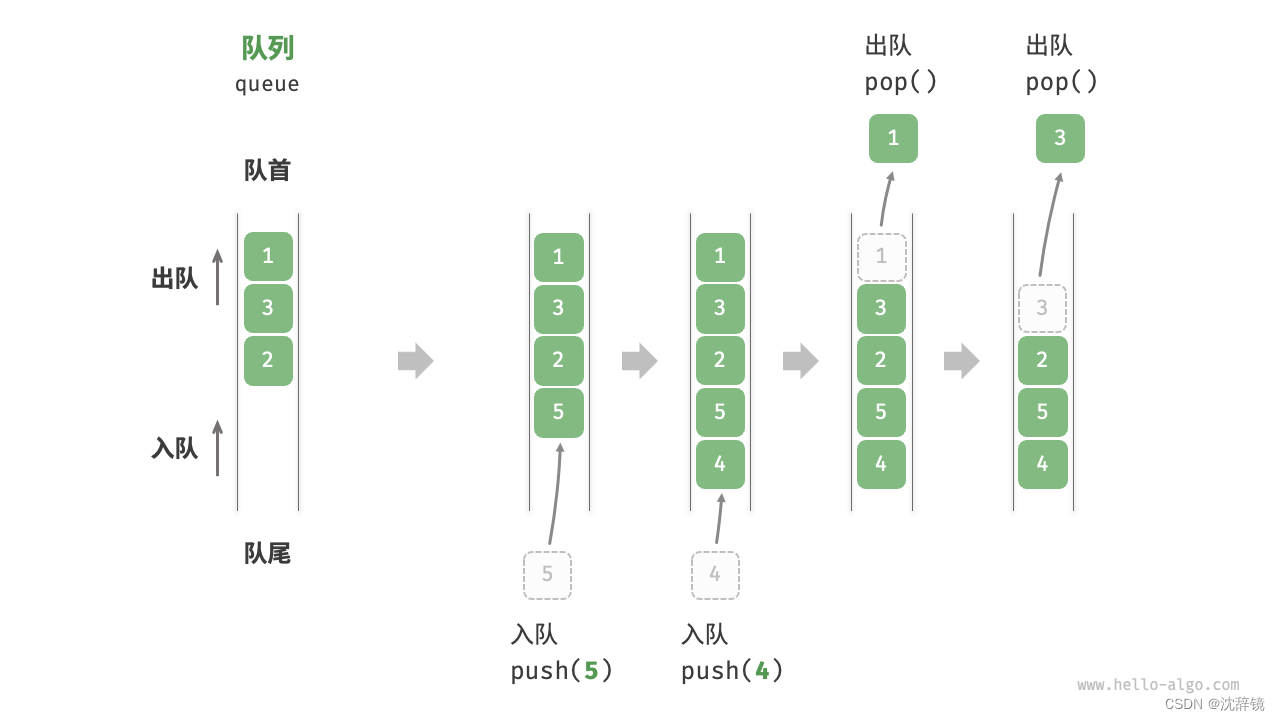
队列基础操作有如下几种：

  1. push 放入（从队尾）
  2. pop 拿出（从队首）
  3. empty 是否为空
  4. size 栈的大小
  5. front
#include <iostream>
using namespace std;

const int N = 100;

int q[N], front = 0, tail = 0;

int main()
{

	//使用数组模拟队列
	int x;
	cin >> x;
	//push 放入队列中
	q[++tail] = x;
	//pop 把元素移除（只能从队首）
	front++;
	//size 队列长度
	int size = tail - front + 1;
	//empty 看size是否为0
	//front 
	return q[front];


	return 0;
}
/* 初始化队列 */
queue<int> queue;

/* 元素入队 */
queue.push(1);
queue.push(3);
queue.push(2);
queue.push(5);
queue.push(4);

/* 访问队首元素 */
int front = queue.front();

/* 元素出队 */
queue.pop();

/* 获取队列的长度 */
int size = queue.size();

/* 判断队列是否为空 */
bool empty = queue.empty();

额外：优先队列，双向队列

http://t.csdnimg.cn/KpFjNicon-default.png?t=N7T8http://t.csdnimg.cn/KpFjN5.2   队列 - Hello 算法 (hello-algo.com)icon-default.png?t=N7T8https://www.hello-algo.com/chapter_stack_and_queue/queue/#5215.3   双向队列 - Hello 算法 (hello-algo.com)icon-default.png?t=N7T8https://www.hello-algo.com/chapter_stack_and_queue/deque/

/* 初始化双向队列 */
deque<int> deque;

/* 元素入队 */
deque.push_back(2);   // 添加至队尾
deque.push_back(5);
deque.push_back(4);
deque.push_front(3);  // 添加至队首
deque.push_front(1);

/* 访问元素 */
int front = deque.front(); // 队首元素
int back = deque.back();   // 队尾元素

/* 元素出队 */
deque.pop_front();  // 队首元素出队
deque.pop_back();   // 队尾元素出队

/* 获取双向队列的长度 */
int size = deque.size();

/* 判断双向队列是否为空 */
bool empty = deque.empty();

双向队列兼具栈与队列的逻辑，因此它可以实现这两者的所有应用场景，同时提供更高的自由度。

我们知道，软件的“撤销”功能通常使用栈来实现：系统将每次更改操作 push 到栈中，然后通过 pop 实现撤销。然而，考虑到系统资源的限制，软件通常会限制撤销的步数（例如仅允许保存 50 步）。当栈的长度超过 50 时，软件需要在栈底（队首）执行删除操作。但栈无法实现该功能，此时就需要使用双向队列来替代栈。请注意，“撤销”的核心逻辑仍然遵循栈的先入后出原则，只是双向队列能够更加灵活地实现一些额外逻辑。

二、DFS深度优先搜索-----栈

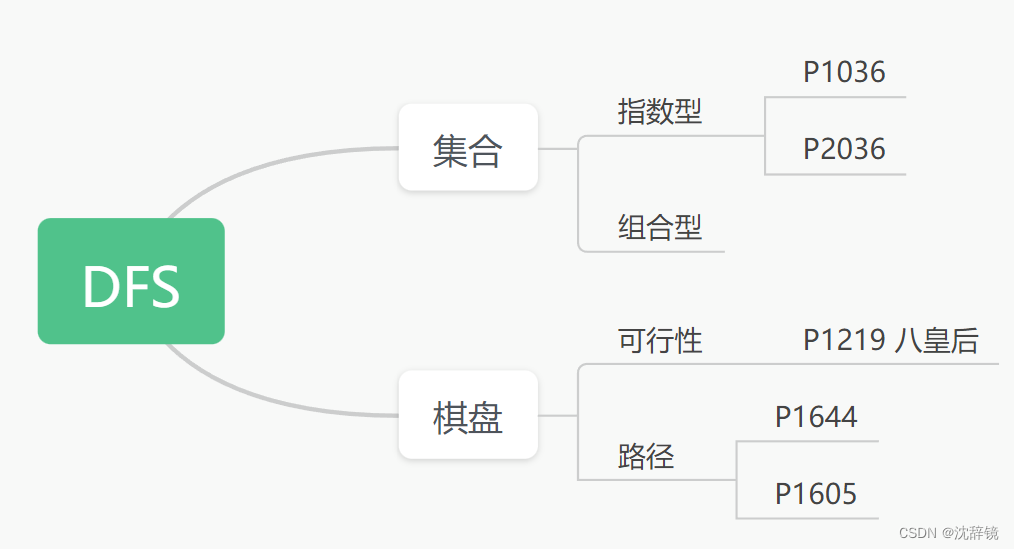 1.指数型搜索

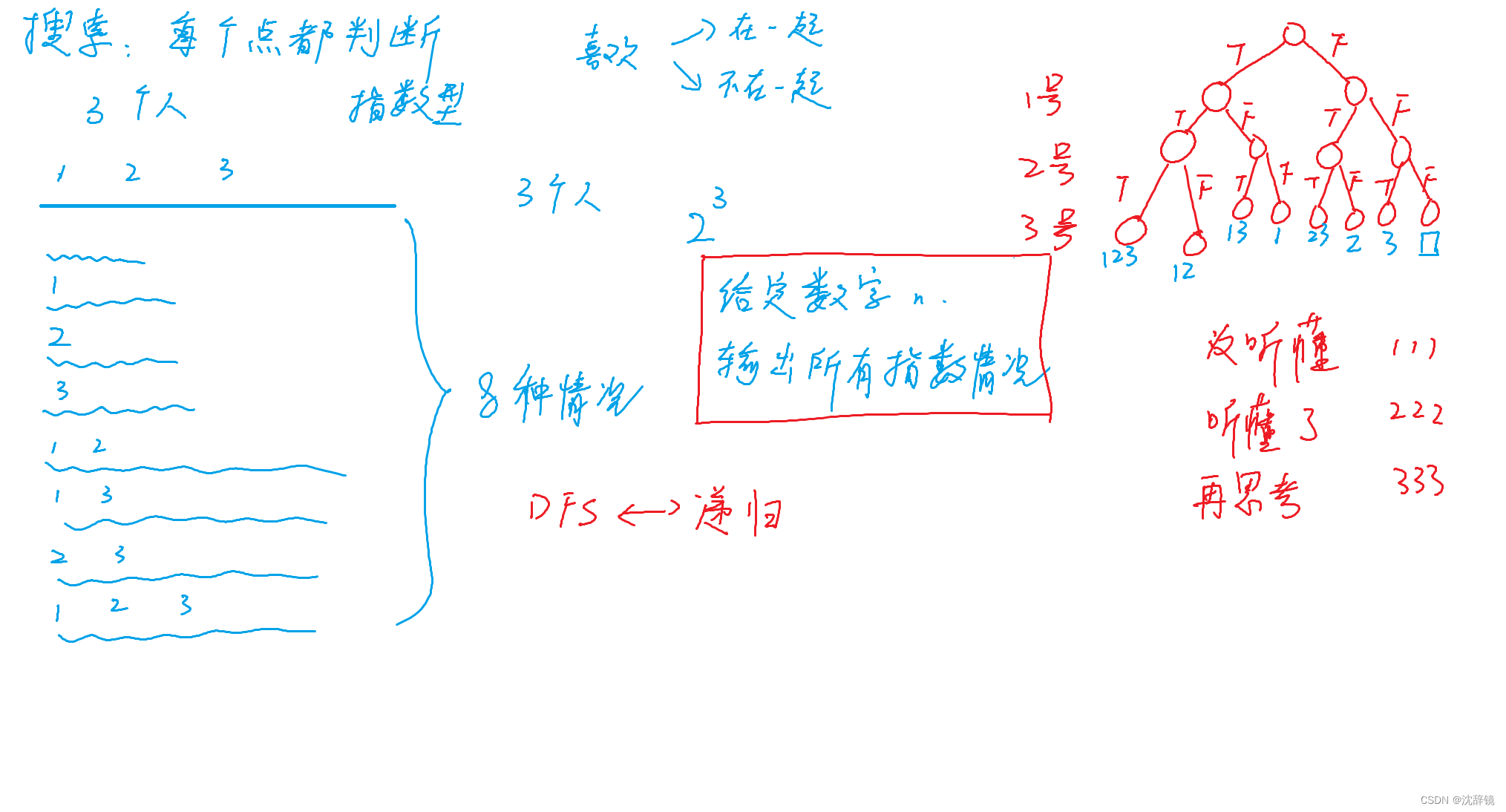
模板：

void dfs(int step){
    判断边界
    尝试每一种可能 for(i=1;i<=n;i++){
        继续下一步 dfs(step+1)
        }
    返回
}

#include <iostream>

using namespace std;

const int N = 100;

int n;//输入的节点数  
int st[N] = {}; //决策数组 0 表示没有搜索过， 1表示选择 ， 2表示没有选择

// 对于每一个点，都需要有一次决策，无论是1还是2 
// 搜索是把所有的情况都考虑 

 // u表示对u进行抉择，已经抉择了u个数
void dfs(int u) {
	// 递归出口，当所有节点都决策完毕时输出结果  
	if (u > n){
		for (int i = 0; i < n; i++) {
			// 只有当第i个节点被选择时才输出 
			if (st[u] = 1){
				cout << i << " ";
			}
		}

	}
	// 选择第u个节点（标记为1）并继续搜索下一个节点
	st[u] = 1;
	dfs(u + 1);

	// 恢复第u个节点的状态（标记为0）并选择不选择第u个节点（标记为2）并继续搜索下一个节点
	st[u] = 0;
	st[u] = 2;
	dfs(u + 1);
	// 继续恢复第u个节点的状态（标记为0）以备下次决策使用  
	st[u] = 0;
}
int main()
{
	cin >> n;

	dfs(1);
	return 0;
}


Python Tutor code visualizer: Visualize code in Python, JavaScript, C, C++, and Javaicon-default.png?t=N7T8https://pythontutor.com/render.html#code=%23include%20%3Ciostream%3E%0A%0Ausing%20namespace%20std%3B%0A%0Aconst%20int%20N%20%3D%20100%3B%0A%0Aint%20n%20,%20st%5BN%5D%20%3D%20%7B%7D%3B%20//%200%20%E8%A1%A8%E7%A4%BA%E6%B2%A1%E6%9C%89%E6%90%9C%E7%B4%A2%E8%BF%87%EF%BC%8C%201%E8%A1%A8%E7%A4%BA%E9%80%89%E6%8B%A9%20%EF%BC%8C%202%E8%A1%A8%E7%A4%BA%E6%B2%A1%E6%9C%89%E9%80%89%E6%8B%A9%0A%0A//%20%E5%AF%B9%E4%BA%8E%E6%AF%8F%E4%B8%80%E4%B8%AA%E7%82%B9%EF%BC%8C%E9%83%BD%E9%9C%80%E8%A6%81%E6%9C%89%E4%B8%80%E6%AC%A1%E5%86%B3%E7%AD%96%EF%BC%8C%E6%97%A0%E8%AE%BA%E6%98%AF1%E8%BF%98%E6%98%AF2%20%0A//%20%E6%90%9C%E7%B4%A2%E6%98%AF%E6%8A%8A%E6%89%80%E6%9C%89%E7%9A%84%E6%83%85%E5%86%B5%E9%83%BD%E8%80%83%E8%99%91%20%0A%0A//%20u%E8%A1%A8%E7%A4%BA%E5%AF%B9u%E8%BF%9B%E8%A1%8C%E6%8A%89%E6%8B%A9%EF%BC%8C%E5%B7%B2%E7%BB%8F%E6%8A%89%E6%8B%A9%E4%BA%86u%E4%B8%AA%E6%95%B0%20%0Avoid%20dfs%28%20int%20u%20%29%20%7B%0A%20%20%20%20%0A%20%20%20%20//%20%E9%80%92%E5%BD%92%E5%87%BA%E5%8F%A3%20%EF%BC%8C%20%E6%AF%8F%E4%B8%80%E4%B8%AA%E7%82%B9%E9%83%BD%E6%8A%89%E6%8B%A9%E8%BF%87%E4%BA%86%20%0A%20%20%20%20if%28u%20%3E%20n%20%29%7B%0A%20%20%20%20%20%20%20%20for%28int%20i%20%3D%201%3B%20i%20%3C%3D%20n%20%3B%20i%2B%2B%20%29%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20//%20%E6%88%91%E4%BB%AC%E5%8F%AA%E6%9C%89%E5%9C%A8%E9%80%89%E6%8B%A9%E7%AC%ACi%E4%B8%AA%E7%82%B9%E7%9A%84%E6%97%B6%E5%80%99%E8%BE%93%E5%87%BA%20%0A%20%20%20%20%20%20%20%20%20%20%20%20if%28st%5Bu%5D%20%3D%3D%201%20%29%20%7B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20cout%20%3C%3C%20i%20%3C%3C%20%22%20%22%20%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20%7D%0A%20%20%20%20%20%20%20%20return%20%3B%0A%20%20%20%20%7D%0A%20%20%20%20%0A%20%20%20%20%0A%20%20%20%20//%20%E9%80%89%E6%8B%A9%0A%20%20%20%20//%20st%5Bu%5D%20%3D%200%3B%20%E8%BF%99%E5%8F%A5%E8%AF%9D%E9%80%9A%E5%B8%B8%E7%9C%81%E7%95%A5%20%0A%20%20%20%20st%5Bu%5D%20%3D%201%3B%0A%20%20%20%20dfs%28u%20%2B%201%29%3B%0A%20%20%20%20%0A%20%20%20%20//%20%E6%81%A2%E5%A4%8D%E7%8E%B0%E5%9C%BA%EF%BC%8C%E6%8E%A7%E5%88%B6%E5%8F%98%E9%87%8F%20%EF%BC%9A%20%E5%8D%95%E4%B8%80%E5%8F%98%E9%87%8F%E5%8E%9F%E5%88%99%20%0A%20%20%20%20st%5Bu%5D%20%3D%200%3B%20%0A%20%20%20%20//%20%E4%B8%8D%E9%80%89%E6%8B%A9%20%0A%20%20%20%20st%5Bu%5D%20%3D%202%3B%0A%20%20%20%20dfs%28u%20%2B%201%29%3B%0A%20%20%20%20%0A%20%20%20%20//%20%E7%BB%A7%E7%BB%AD%E6%81%A2%E5%A4%8D%E7%8E%B0%E5%9C%BA%0A%20%20%20%20st%5Bu%5D%20%3D%200%3B%20%0A%7D%0A%0Aint%20main%28%29%7B%0A%20%20n%3D3%3B%0A%20%20%20%20dfs%281%29%3B%0A%20%20%20%20%0A%20%20%20%20return%200%3B%0A%7D&cppShowMemAddrs=true&cumulative=false&curInstr=38&heapPrimitives=nevernest&mode=display&origin=opt-frontend.js&py=cpp_g%2B%2B9.3.0&rawInputLstJSON=%5B%5D&textReferences=false

例题1 P2036 Perket

 

#include <iostream>  
#include <algorithm>  
#include <cstdio>  
#include <cmath>  
using namespace std;  
  
// 全局变量声明  
int n; // n代表数字的个数  
int mindif = 999999999; // mindif用于存储最小差值，初始化为一个非常大的数  
int s[10], b[10]; // s数组和b数组分别用于存储输入的数字和它们对应的值  
  
// perket函数是一个递归函数，用于计算所有可能的组合  
// u代表当前处理的数字的索引  
// sp代表当前选择的s数组中数字的乘积  
// bs代表当前选择的b数组中数字的和  
void perket(int u, int sp, int bs) {  
    // 递归终止条件：当u大于n时，表示所有数字都已经处理完毕  
    if (u > n) {  
        // 如果bs为0，表示没有选择任何b数组中的数字，直接返回  
        if (!bs) {  
            return;  
        }  
        // 更新最小差值  
        mindif = min(mindif, abs(sp - bs));  
        return;  
    }  
      
    // 递归调用1：不选择当前数字  
    perket(u + 1, sp, bs);  
      
    // 递归调用2：选择当前数字  
    perket(u + 1, sp * s[u], bs + b[u]);  
}  
  
int main() {  
    // 输入数字的个数  
    cin >> n;  
      
    // 输入每个数字及其对应的值  
    for (int i = 1; i <= n; i++) {  
        cin >> s[i] >> b[i];  
    }  
      
    // 调用perket函数开始计算  
    perket(1, 1, 0);  
      
    // 输出最小差值  
    cout << mindif << endl;  
      
    return 0;  
}

Python Tutor code visualizer: Visualize code in Python, JavaScript, C, C++, and Javaicon-default.png?t=N7T8https://pythontutor.com/render.html#code=%23include%20%3Ciostream%3E%20%20%0A%23include%20%3Calgorithm%3E%20%20%0A%23include%20%3Ccstdio%3E%20%20%0A%23include%20%3Ccmath%3E%20%20%0Ausing%20namespace%20std%3B%20%20%0A%20%20%0A//%20%E5%85%A8%E5%B1%80%E5%8F%98%E9%87%8F%E5%A3%B0%E6%98%8E%20%20%0Aint%20n%3B%20//%20n%E4%BB%A3%E8%A1%A8%E6%95%B0%E5%AD%97%E7%9A%84%E4%B8%AA%E6%95%B0%20%20%0Aint%20mindif%20%3D%20999999999%3B%20//%20mindif%E7%94%A8%E4%BA%8E%E5%AD%98%E5%82%A8%E6%9C%80%E5%B0%8F%E5%B7%AE%E5%80%BC%EF%BC%8C%E5%88%9D%E5%A7%8B%E5%8C%96%E4%B8%BA%E4%B8%80%E4%B8%AA%E9%9D%9E%E5%B8%B8%E5%A4%A7%E7%9A%84%E6%95%B0%20%20%0Aint%20s%5B10%5D,%20b%5B10%5D%3B%20//%20s%E6%95%B0%E7%BB%84%E5%92%8Cb%E6%95%B0%E7%BB%84%E5%88%86%E5%88%AB%E7%94%A8%E4%BA%8E%E5%AD%98%E5%82%A8%E8%BE%93%E5%85%A5%E7%9A%84%E6%95%B0%E5%AD%97%E5%92%8C%E5%AE%83%E4%BB%AC%E5%AF%B9%E5%BA%94%E7%9A%84%E5%80%BC%20%20%0A%20%20%0A//%20perket%E5%87%BD%E6%95%B0%E6%98%AF%E4%B8%80%E4%B8%AA%E9%80%92%E5%BD%92%E5%87%BD%E6%95%B0%EF%BC%8C%E7%94%A8%E4%BA%8E%E8%AE%A1%E7%AE%97%E6%89%80%E6%9C%89%E5%8F%AF%E8%83%BD%E7%9A%84%E7%BB%84%E5%90%88%20%20%0A//%20u%E4%BB%A3%E8%A1%A8%E5%BD%93%E5%89%8D%E5%A4%84%E7%90%86%E7%9A%84%E6%95%B0%E5%AD%97%E7%9A%84%E7%B4%A2%E5%BC%95%20%20%0A//%20sp%E4%BB%A3%E8%A1%A8%E5%BD%93%E5%89%8D%E9%80%89%E6%8B%A9%E7%9A%84s%E6%95%B0%E7%BB%84%E4%B8%AD%E6%95%B0%E5%AD%97%E7%9A%84%E4%B9%98%E7%A7%AF%20%20%0A//%20bs%E4%BB%A3%E8%A1%A8%E5%BD%93%E5%89%8D%E9%80%89%E6%8B%A9%E7%9A%84b%E6%95%B0%E7%BB%84%E4%B8%AD%E6%95%B0%E5%AD%97%E7%9A%84%E5%92%8C%20%20%0Avoid%20perket%28int%20u,%20int%20sp,%20int%20bs%29%20%7B%20%20%0A%20%20%20%20//%20%E9%80%92%E5%BD%92%E7%BB%88%E6%AD%A2%E6%9D%A1%E4%BB%B6%EF%BC%9A%E5%BD%93u%E5%A4%A7%E4%BA%8En%E6%97%B6%EF%BC%8C%E8%A1%A8%E7%A4%BA%E6%89%80%E6%9C%89%E6%95%B0%E5%AD%97%E9%83%BD%E5%B7%B2%E7%BB%8F%E5%A4%84%E7%90%86%E5%AE%8C%E6%AF%95%20%20%0A%20%20%20%20if%20%28u%20%3E%20n%29%20%7B%20%20%0A%20%20%20%20%20%20%20%20//%20%E5%A6%82%E6%9E%9Cbs%E4%B8%BA0%EF%BC%8C%E8%A1%A8%E7%A4%BA%E6%B2%A1%E6%9C%89%E9%80%89%E6%8B%A9%E4%BB%BB%E4%BD%95b%E6%95%B0%E7%BB%84%E4%B8%AD%E7%9A%84%E6%95%B0%E5%AD%97%EF%BC%8C%E7%9B%B4%E6%8E%A5%E8%BF%94%E5%9B%9E%20%20%0A%20%20%20%20%20%20%20%20if%20%28!bs%29%20%7B%20%20%0A%20%20%20%20%20%20%20%20%20%20%20%20return%3B%20%20%0A%20%20%20%20%20%20%20%20%7D%20%20%0A%20%20%20%20%20%20%20%20//%20%E6%9B%B4%E6%96%B0%E6%9C%80%E5%B0%8F%E5%B7%AE%E5%80%BC%20%20%0A%20%20%20%20%20%20%20%20mindif%20%3D%20min%28mindif,%20abs%28sp%20-%20bs%29%29%3B%20%20%0A%20%20%20%20%20%20%20%20return%3B%20%20%0A%20%20%20%20%7D%20%20%0A%20%20%20%20%20%20%0A%20%20%20%20//%20%E9%80%92%E5%BD%92%E8%B0%83%E7%94%A81%EF%BC%9A%E4%B8%8D%E9%80%89%E6%8B%A9%E5%BD%93%E5%89%8D%E6%95%B0%E5%AD%97%20%20%0A%20%20%20%20perket%28u%20%2B%201,%20sp,%20bs%29%3B%20%20%0A%20%20%20%20%20%20%0A%20%20%20%20//%20%E9%80%92%E5%BD%92%E8%B0%83%E7%94%A82%EF%BC%9A%E9%80%89%E6%8B%A9%E5%BD%93%E5%89%8D%E6%95%B0%E5%AD%97%20%20%0A%20%20%20%20perket%28u%20%2B%201,%20sp%20*%20s%5Bu%5D,%20bs%20%2B%20b%5Bu%5D%29%3B%20%20%0A%7D%20%20%0A%20%20%0Aint%20main%28%29%20%7B%20%20%0A%20%20%20%20//%20%E8%BE%93%E5%85%A5%E6%95%B0%E5%AD%97%E7%9A%84%E4%B8%AA%E6%95%B0%20%20%0A%20%20%20%20n%3D4%3B%0A%20%20%20%20%20%20%0A%20%20%20%20//%20%E8%BE%93%E5%85%A5%E6%AF%8F%E4%B8%AA%E6%95%B0%E5%AD%97%E5%8F%8A%E5%85%B6%E5%AF%B9%E5%BA%94%E7%9A%84%E5%80%BC%20%20%0A%20%20%20%20s%5B0%5D%3D1,s%5B1%5D%3D2,s%5B2%5D%3D3,s%5B3%5D%3D4%3B%0A%20%20%20%20b%5B0%5D%3D7,b%5B1%5D%3D6,b%5B2%5D%3D8,b%5B3%5D%3D9%3B%0A%20%20%20%20%20%20%0A%20%20%20%20//%20%E8%B0%83%E7%94%A8perket%E5%87%BD%E6%95%B0%E5%BC%80%E5%A7%8B%E8%AE%A1%E7%AE%97%20%20%0A%20%20%20%20perket%281,%201,%200%29%3B%20%20%0A%20%20%20%20%20%20%0A%20%20%20%20//%20%E8%BE%93%E5%87%BA%E6%9C%80%E5%B0%8F%E5%B7%AE%E5%80%BC%20%20%0A%20%20%20%20cout%20%3C%3C%20mindif%20%3C%3C%20endl%3B%20%20%0A%20%20%20%20%20%20%0A%20%20%20%20return%200%3B%20%20%0A%7D&cppShowMemAddrs=true&cumulative=false&curInstr=0&heapPrimitives=nevernest&mode=display&origin=opt-frontend.js&py=cpp_g%2B%2B9.3.0&rawInputLstJSON=%5B%5D&textReferences=false

在给定的代码中，每次递归的两种选择（选择当前数字和不选择当前数字）可能会产生重复的结果。这意味着，递归函数perket可能会计算出重复的组合。

为了解决这个问题，可以在递归过程中添加一些逻辑来跳过已经计算过的组合，或者使用其他方法来避免重复计算。例如，可以维护一个集合或哈希集合来跟踪已经计算过的组合，并在递归函数中进行检查。

如果不采取措施避免重复计算，则可能会导致递归函数的时间复杂度增加，因为重复计算相同的组合会导致更多的递归调用。在处理大量数据时，这可能会导致性能问题。

2.组合型搜索

例题2 全排列

【题意】
先给一个正整数 ( 1 < = n < = 10 )，输出所有全排列。
什么是全排列，例如n＝3，输出所有组合,并且按字典序输出：
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
每个全排列一行，相邻两个数用空格隔开（最后一个数后面没有空格）
【输入格式】
一行一个整数n。
【输出格式】
输出1~n的所有全排列。
【样例输入】
3
【样例输出】
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

#include <iostream>  // 引入输入输出流库  
#include <algorithm>  // 引入算法库  
#include <cstdio>      // 引入标准输入输出库  
#include <cmath>        // 引入数学库  
using namespace std;     // 使用标准命名空间  
  
int n, ans[10], used[10];   // 定义全局变量，n表示要选取的数字个数，ans数组用于存放结果，used数组用于标记数字是否被使用过  
  
void dfs(int cnt){          // 定义深度优先搜索函数，cnt表示当前已经选取的数字个数  
    if (cnt > n) {           // 如果已经选取的数字个数大于n，说明已经选取了所有数字，输出结果并返回  
        for (int i = 1; i <= n; i++) { // 遍历所有数字并输出  
            cout << ans[i] << " ";  
        }  
        cout << endl;  
        return;  
    }  
    for (int i = 1; i <= n; i++){ // 枚举所有数字  
        if (used[i] == 0) {      // 如果数字i还没有被使用过  
            ans[cnt] = i;        // 将数字i放入当前位置  
            used[i] = 1;          // 标记数字i为已使用  
            dfs(cnt + 1);        // 递归搜索下一个位置  
               
            ans[cnt] = 0;         // 撤销当前位置的选择，即清空当前位置  
            used[i] = 0;           // 撤销对数字i的选择，即将其标记为未使用  
        }  
    }  
}  
  
int main() {                  // 主函数  
    cin >> n;                  // 输入要选取的数字个数n  
    dfs(1);                     // 从第一个位置开始搜索  
    return 0;                   // 程序正常结束  
}

这段代码中的回溯是通过以下步骤实现的：

1. 在dfs函数中，首先检查是否已经选取了所有数字（即`cnt`是否大于`n`）。如果是，则输出当前结果并返回。
2. 然后，函数使用一个循环来枚举所有数字。如果某个数字还没有被使用过（即`used[i]`等于0），则进行以下操作：

  •     将该数字放入当前位置（即`ans[cnt] = i`）。
  •     标记该数字为已使用（即`used[i] = 1`）。
  •     递归调用`dfs(cnt + 1)`来搜索下一个位置。

3. 在递归调用返回后，执行回溯操作：

  •     撤销当前位置的选择，即将`ans[cnt]`重置为0，表示该位置还没有被选择。
  •     撤销对数字`i`的选择，即将`used[i]`重置为0，表示数字`i`现在可以再次被选择。

4. 重复上述过程，直到所有可能的排列都被探索完为止。

通过这种方式，代码能够撤销之前的决策，尝试其他可能的路径，从而全面地探索所有可能的解空间。

还有几个题，以后补补（太赶了qaq

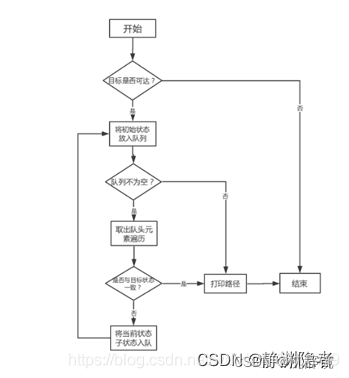
三、BFS广度优先搜索-----队列

bfs个人感觉就是，同时往每个方向都试试，最先得到的就是最好的。

它是一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。宽度优先搜索是一种对图进行搜索的算法。假设我们一开始位于某个顶点（即起点），此 时并不知道图的整体结构，而我们的目的是从起点开始顺着边搜索，直到到达指定顶点（即终 点）。在此过程中每走到一个顶点，就会判断一次它是否为终点。广度优先搜索会优先从离起点 近的顶点开始搜索。

b站有个视频非常清晰，这里贴下链接

【广度优先搜索BFS遍历-动画演示过程，希望对大家有所帮助~】

https://www.bilibili.com/video/BV1bP4y1K7Tr?vd_source=7ccfb0770f378b7710213a50fbacfc17icon-default.png?t=N7T8https://www.bilibili.com/video/BV1bP4y1K7Tr?vd_source=7ccfb0770f378b7710213a50fbacfc17

这个大佬写的也很清晰：

http://t.csdnimg.cn/sw4pZicon-default.png?t=N7T8http://t.csdnimg.cn/sw4pZ

int BFS(Node start, Node target) {
    入队(初始状态);
    visited[初始状态] = true;
    while(!空队) {
        for() { // 状态转换
            Node node = 队首元素;
 
            对node的处理，生成新node状态;
 
            if (visited[node] == true)
                continue;
            if (node == target) {
                输出答案;
                return 0;
            }
            v[node] = true;
            入队(node);
        }
    出队();
    }
    
}

 例题3 P1135 奇怪的电梯

#include <iostream>  // 引入输入输出流    
#include <cstring>  // 引入C风格的字符串处理函数库，用于memset  
#include <queue>  // 引入队列容器  
using namespace std;  
  
const int N = 201;  // 定义常量N为201，表示图的最大节点数  
  
int n, a, b;  // n为图的节点数，a为起点，b为终点  
int k[N], vis[N], ans[N];  // k数组存储每个节点的关联值，vis数组标记节点是否被访问过，ans数组存储从起点到每个节点的最短路径长度  
  
// BFS函数，从节点a开始搜索  
void bfs(int a) {  
    queue<int> Q;  // 定义一个队列Q  
    Q.push(a);  // 将起点a加入队列  
    ans[a] = 0;  // 设置起点a到自身的距离为0  
  
    // 当队列不为空时继续循环  
    while (!Q.empty()) {  
        int u = Q.front();  // 取出队首元素  
        Q.pop();  // 弹出队首元素  
  
        // 如果当前节点是目标节点b，则结束搜索  
        if (u == b) {  
            break;  
        }  
        // 如果当前节点已经被访问过，则跳过  
        if (vis[u] == 1) {  
            continue;  
        }  
  
        vis[u] = 1;  // 标记当前节点为已访问  
  
        // 计算通过当前节点的关联值k[u]可以到达的两个节点v1和v2  
        int v1 = u + k[u];  
        // 如果v1是一个有效的节点且未被访问过，则将其加入队列，并更新ans[v1]  
        if (v1 >= 1 && v1 <= n && vis[v1] == 0) {  
            Q.push(v1);  
            ans[v1] = min(ans[v1], ans[u] + 1);  
        }  
  
        int v2 = u - k[u];  
        // 如果v2是一个有效的节点且未被访问过，则将其加入队列，并更新ans[v2]  
        if (v2 >= 1 && v2 <= n && vis[v2] == 0) {  
            Q.push(v2);  
            ans[v2] = min(ans[v2], ans[u] + 1);  
        }  
    }  
}  
  
int main() {  
    cin >> n >> a >> b;  // 输入节点数n，起点a和终点b  
  
    // 初始化ans数组为一个很大的数（表示无穷大）  
    memset(ans, 0x3f, sizeof(ans));  
  
    // 输入每个节点的关联值k[i]  
    for (int i = 1; i <= n; i++) {  
        cin >> k[i];  
    }  
  
    bfs(a);  // 从起点a开始BFS搜索  
  
    // 如果从a到b没有路径，则输出-1，否则输出最短路径长度  
    if (ans[b] == 1e9) {  
        cout << -1 << endl;  
    } else {  
        cout << ans[b] << endl;  
    }  
    return 0;  
}

四、BFS与DFS区别

bfs 遍历节点是先进先出，dfs遍历节点是先进后出；
bfs是按层次访问的，dfs 是按照一个路径一直访问到底，当前节点没有未访问的邻居节点时，然后回溯到上一个节点，不断的尝试，直到访问到目标节点或所有节点都已访问。
bfs 适用于求源点与目标节点距离最近的情况，例如：求最短路径。dfs 更适合于求解一个任意符合方案中的一个或者遍历所有情况，例如：全排列、拓扑排序、求到达某一点的任意一条路径。
————————————————

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
                        
原文链接：https://blog.csdn.net/aliyonghang/article/details/128724989

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1430992.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

车载以太网：PHY（物理层）介绍

车载以太网：PHY（物理层）介绍

0 工具准备 TJA1101B芯片手册 TJA1101B automotive Ethernet PHY手册 IEEE802.3-2018.pdf 1 车载以太网PHY&#xff08;物理层&#xff09;介绍 常见的普通以太网分为10BASE-2、10/100BASE-TX和1000BASE-T&#xff0c;一般都使用RJ45接口&#xff0c;对于1000BASE-T来说&#…
阅读更多...
LabVIEW风力发电机在线监测

LabVIEW风力发电机在线监测

LabVIEW风力发电机在线监测 随着可再生能源的发展&#xff0c;风力发电成为越来越重要的能源形式。设计了一个基于控制器局域网&#xff08;CAN&#xff09;总线和LabVIEW的风力发电机在线监测系统&#xff0c;实现风力发电机的实时监控和故障诊断&#xff0c;以提高风力发电的…
阅读更多...
Python使用zdppy_es国产框架操作Elasticsearch实现增删改查

Python使用zdppy_es国产框架操作Elasticsearch实现增删改查

Python使用zdppy_es国产框架操作Elasticsearch实现增删改查 本套教程配套有录播课程和私教课程，欢迎私信我。 Docker部署ElasticSearch7 创建基本容器 docker run -itd --name elasticsearch -p 9200:9200 -e "discovery.type=single-node" -e ES_JAVA_OPTS=&quo…
阅读更多...
上位机图像处理和嵌入式模块部署（linux开发板的选择）

上位机图像处理和嵌入式模块部署（linux开发板的选择）

【 声明&#xff1a;版权所有&#xff0c;欢迎转载&#xff0c;请勿用于商业用途。 联系信箱&#xff1a;feixiaoxing 163.com】 很多图像算法是通过上位机来完成的&#xff0c;比如说工业视觉当中的halcon&#xff0c;一般都是要运行在windows平台上面&#xff0c;并且需要高性…
阅读更多...
Blender教程（基础）-面的填充-13

Blender教程（基础）-面的填充-13

一、准备 新建一个立方&#xff0c;删除其中一个面。 二、三角面填充 首先是编辑模式下&#xff0c;选择需要填充的所有边。 鼠标右键弹出填充 填充完是以三角面的形式填充的 编辑模式下&#xff0c;面选择模式&#xff0c;选择刚才填充的两个三角面&#xff0c;然后右键…
阅读更多...
谈谈BlueStore

谈谈BlueStore

目录 未完待续前言组成前期准备工作基础概念对象PextentextentBlobNode 线程事务磁盘的抽象与分配位图法分层位图 上电流程写流程读流程参考资料 未完待续 前言 BlueStore是什么&#xff1f; Ceph是一个统一的分布式存储系统。BlueStore是Ceph的存储引擎。 它的作用是什么&am…
阅读更多...
STM32标准库——（10）ADC模数转换器

STM32标准库——（10）ADC模数转换器

1.ADC简介 12位ADC是一种逐次逼近型模拟数字转换器。它有多达18个通道&#xff0c;可测量16个外部和2个内部信号源。各通道的A/D转换可以单次、连续、扫描或间断模式执行。ADC的结果可以左对齐或右对齐方式存储在16位数据寄存器中。 模拟看门狗特性允许应用程序检测输入电压是…
阅读更多...
蓝桥杯省赛无忧 课件80 第12次学长带练笔记

蓝桥杯省赛无忧 课件80 第12次学长带练笔记

阅读更多...
[机器学习]LFM梯度下降算法

[机器学习]LFM梯度下降算法

一.LFM梯度下降算法 2.代码实现 # 0. 引入依赖 import numpy as np import pandas as pd# 1. 数据准备 # 评分矩阵R R np.array([[4,0,2,0,1],[0,2,3,0,0],[1,0,2,4,0],[5,0,0,3,1],[0,0,1,5,1],[0,3,2,4,1],]) # 0分表示还未进行评价 # 二维数组小技巧&#xff1a;取行数R.s…
阅读更多...
云端录制直播流视频，上传云盘

云端录制直播流视频，上传云盘

前言 哪一天我心血来潮&#xff0c;想把我儿子学校的摄像头视频流录制下来&#xff0c;并保存到云盘上&#xff0c;这样我就可以在有空的时候看看我儿子在学校干嘛。想到么就干&#xff0c;当时花了一些时间开发了一个后端服务&#xff0c;通过数据库配置录制参数&#xff0c;…
阅读更多...
JavaScript鼠标拖放(Drag and Drop)

JavaScript鼠标拖放(Drag and Drop)

&#x1f9d1;‍&#x1f393; 个人主页&#xff1a;《爱蹦跶的大A阿》 &#x1f525;当前正在更新专栏&#xff1a;《VUE》 、《JavaScript保姆级教程》、《krpano》、《krpano中文文档》 ​ ​ ✨ 前言 拖放是现代界面不可或缺的交互方式之一。本文将介绍如何用JavaScript…
阅读更多...
Redis核心技术与实战【学习笔记】 - 19.Pika：基于SSD实现大容量“Redis”

Redis核心技术与实战【学习笔记】 - 19.Pika：基于SSD实现大容量“Redis”

前言 随着业务数据的增加&#xff08;比如电商业务中&#xff0c;随着用户规模和商品数量的增加&#xff09;&#xff0c;就需要 Redis 能保存更多的数据。你可能会想到使用 Redis 切片集群&#xff0c;把数据分散保存到不同的实例上。但是这样做的话&#xff0c;如果要保存的…
阅读更多...
C# 程序不显示控制台

C# 程序不显示控制台

C# 程序不显示控制台。 C# 使用代码隐藏控制台。 文章目录 代码效果 代码 class Program {// 导入kernel32.dll库中的AllocConsole函数[DllImport("kernel32.dll")]static extern bool AllocConsole();// 导入kernel32.dll库中的FreeConsole函数[DllImport("k…
阅读更多...
鸿蒙（HarmonyOS）项目方舟框架（ArkUI）之Menu组件

鸿蒙（HarmonyOS）项目方舟框架（ArkUI）之Menu组件

鸿蒙&#xff08;HarmonyOS&#xff09;项目方舟框架&#xff08;ArkUI&#xff09;之Menu组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、Menu组件 TextClock组件通过文本将当前系统时间显示在设备上。支持不同时区的时间…
阅读更多...
Mysql运维篇（四） MySQL常用命令

Mysql运维篇（四） MySQL常用命令

一路走来&#xff0c;所有遇到的人&#xff0c;帮助过我的、伤害过我的都是朋友&#xff0c;没有一个是敌人。如有侵权&#xff0c;请留言&#xff0c;我及时删除&#xff01; 一、MySQL命令速查表 https://www.cnblogs.com/pyng/p/15560059.html Mysql DBA运维命令大全 - 墨…
阅读更多...
记录Git无法连接Github（443报错）的一种可能——代理问题

记录Git无法连接Github（443报错）的一种可能——代理问题

参考文章&#xff1a; Git安装配置与使用&#xff08;超级详细&#xff09;_git配置-CSDN博客 github代理报错_valueerror: unable to determine socks version from-CSDN博客 速通 如果在使用 git 时遇到了这样的报错&#xff1a; OpenSSL SSL_connect: SSL_ERROR_SYSCAL…
阅读更多...
[office] excel表格怎么绘制股票的CCI指标- #媒体#学习方法#笔记

[office] excel表格怎么绘制股票的CCI指标- #媒体#学习方法#笔记

excel表格怎么绘制股票的CCI指标? excel表格怎么绘制股票的CCI指标&#xff1f;excel表格中想要绘制一个股票cci指标&#xff0c;该怎么绘制呢&#xff1f;下面我们就来看看详细的教程&#xff0c;需要的朋友可以参考下 CCI指标是一种在股票&#xff0c;贵金属&#xff0c;货…
阅读更多...
嵌入式软件工程师面试题——嵌入式专题 (五十二)

嵌入式软件工程师面试题——嵌入式专题 (五十二)

说明&#xff1a; 面试群&#xff0c;群号&#xff1a; 228447240面试题来源于网络书籍&#xff0c;公司题目以及博主原创或修改&#xff08;题目大部分来源于各种公司&#xff09;&#xff1b;文中很多题目&#xff0c;或许大家直接编译器写完&#xff0c;1分钟就出结果了。但…
阅读更多...
【新书推荐】5.2 位运算符

【新书推荐】5.2 位运算符

本节必须掌握的知识点&#xff1a; 位运算 示例十七 代码分析 汇编解析 5.2.1 位运算 位运算符如表5-2所示&#xff1a; 运算符 作用 示例 & 按位与 两个操作数同时为1&#xff0c;结果为1&#xff1b; | 按位或 两个操作数只要有一个为1&#xff0c;结果就为1&a…
阅读更多...
Apollo配置中心之Server端

Apollo配置中心之Server端

一、通知机制 二、架构思考 1、配置变更如何通知客户端&#xff1f; &#xff08;1&#xff09;如何建立长轮询&#xff1f; 2、客户端如何拉取数据&#xff1f; &#xff08;1&#xff09;如何拉取数据&#xff1f; 3、如何发现变更数据&#xff1f; &#xff08;1&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023